Descente de charges : résoudre un problème

La réalisation d’une descente de charges permet de dimensionner les éléments de la structure porteuse d’un bâtiment. Elle permet de choisir ou de contrôler si la forme, l’épaisseur et le matériau de chaque élément structural sont adaptés.

La descente de charges permet également de s’assurer que le bâtiment ne s’enfonce pas dans le sol.

Quelques formules sont nécessaires afin de mener une descente de charges.

La contrainte σ subie par un élément structural se calcule avec la formule suivante.

avec : σ la contrainte subie par l’élément structural, en N·m–2 ou en Pa F la force de compression, en N A est l’aire de la surface de la section de l’élément, en m2

Cette contrainte, multipliée par un coefficient de sécurité K, est ensuite comparée à la limite d’élasticité, R_ec du matériau de l’élément.

La pression p_{élément/sol} exercée par un élément sur le sol, qui peut faire s’enfoncer cet élément, se calcule avec la formule suivante.

avec : pélément/sol la pression exercée par un élément sur le sol, en N·m–2 ou en Pa P le poids supporté par l’élément, en N A l’aire de la surface en contact avec le sol de l’élément, en m2

Cette pression, multipliée par un coefficient de sécurité K, est ensuite comparée à la résistance à l’enfoncement du sol, R_enf.

On va effectuer une descente de charges sur la maison modélisée ci-dessous.

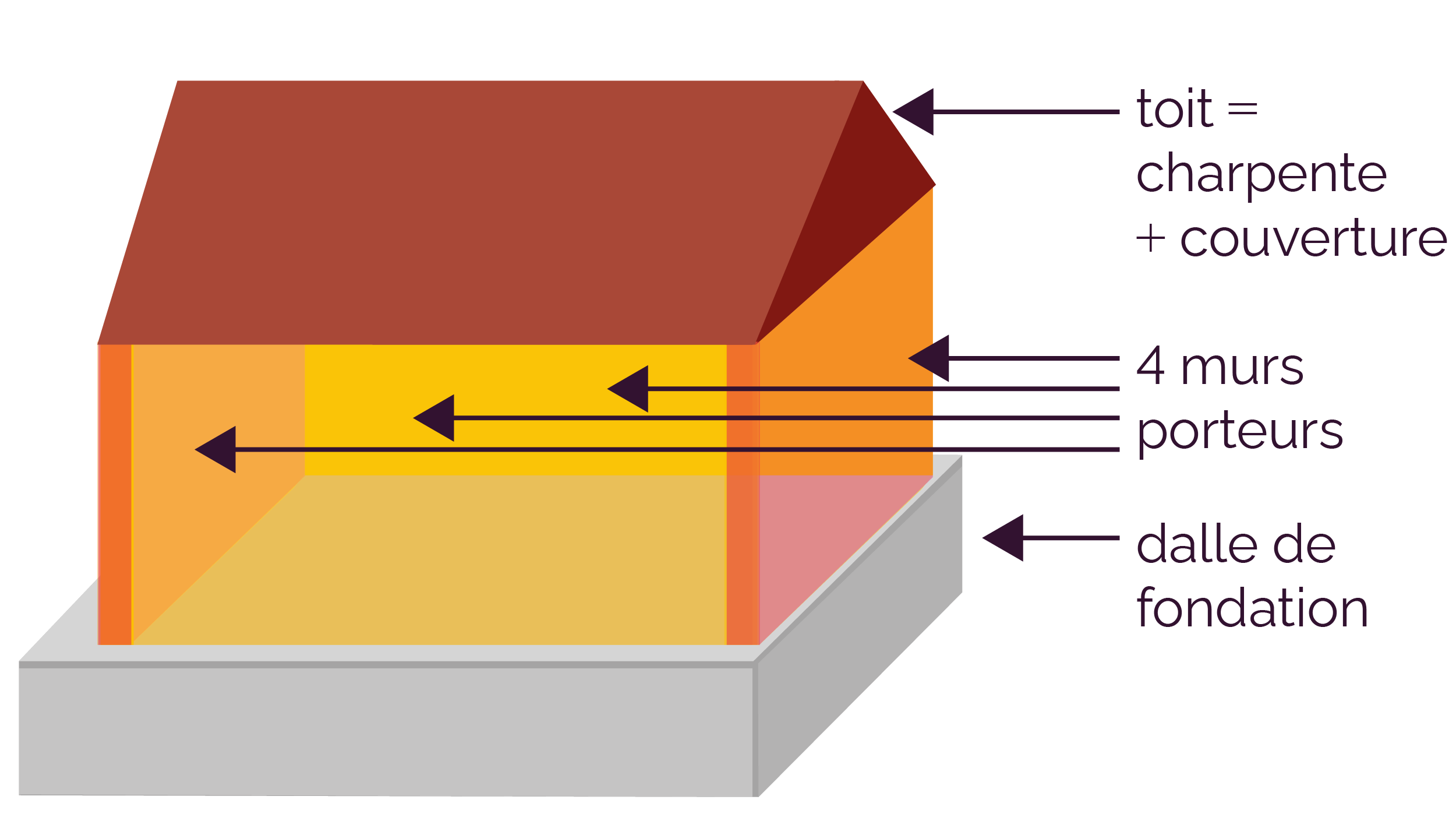
Les plans et les choix de matériaux sont déjà faits, l’objectif est de :

• vérifier que les éléments structuraux de la maison pourront supporter les charges qu’ils vont subir, en tenant compte d’un coefficient de sécurité K = 1,5 ;
• vérifier si le sol supportera le poids de la maison, avec un coefficient de sécurité K = 1,5.

Élément	Matériau	Dimensions (en m)	Masse (en kg)
Toit	Tuiles, chêne et pin	Longueur : 12 Largeur : 6 Hauteur : 2	7400
Mur de façade	Parpaing	Longueur : 12 Largeur : 0,2 Hauteur : 2,4
Mur de pignon	Parpaing	Longueur : 6 Largeur : 0,2 Hauteur : 2,4
Dalle de fondation	Béton	Longueur : 14 Largeur : 8 Hauteur : 0,6

Les matériaux utilisés ont les caractéristiques suivantes :

• Parpaing : ρ = 1750 kg·m^–3 et R_ec= 40 MPa
• Béton : ρ = 2300 kg·m^–3 et R_ec = 15 MPa

On a les charges suivantes.

• Surcharges d’exploitation, subies par la dalle de fondation : Q = 200 N·m^–2.
• Surcharges climatiques liées à la neige, subies par le toit : S = 300 N·m^–2.

Enfin, la résistance à l’enfoncement dans le sol du sol est R_enf= 0,3 MPa.

Voici la méthode pour réaliser la descente de charges de cette maison. Le principe est de s’intéresser aux charges des différents éléments de la maison, du haut vers le bas.

La neige va se déposer sur le toit, on commence donc par calculer son poids.

Si on projette horizontalement le toit, il a une surface dont l’aire vaut :

A_toit= L_toit × l_toit

A_toit= 12 × 6 = 72 m²

L’ensemble de la neige qui peut se déposer sur le toit a un poids P_neige.

Ce poids se calcule en multipliant la surface A_toit (m²) par la surcharge climatique S liée à la neige (en N·m^–2), qui représente le poids d’1 m² de neige :

P_neige= A_toit × S

P_neige= 72 × 300 = 21 600 N

Pour le toit, les données indiquent une masse de 7400 kg.

On a donc :

P_toit= M_toit × g

P_toit= 7400 × 9,81 = 72 600 N

On a donc un poids total, pour la neige et le toit :

P_t+n = P_toit + P_neige

P_t+n = 21 600 + 72 600 ≈ 94 200 N

On détermine les zones d’influence de chaque mur en dessinant le schéma ci-dessous.

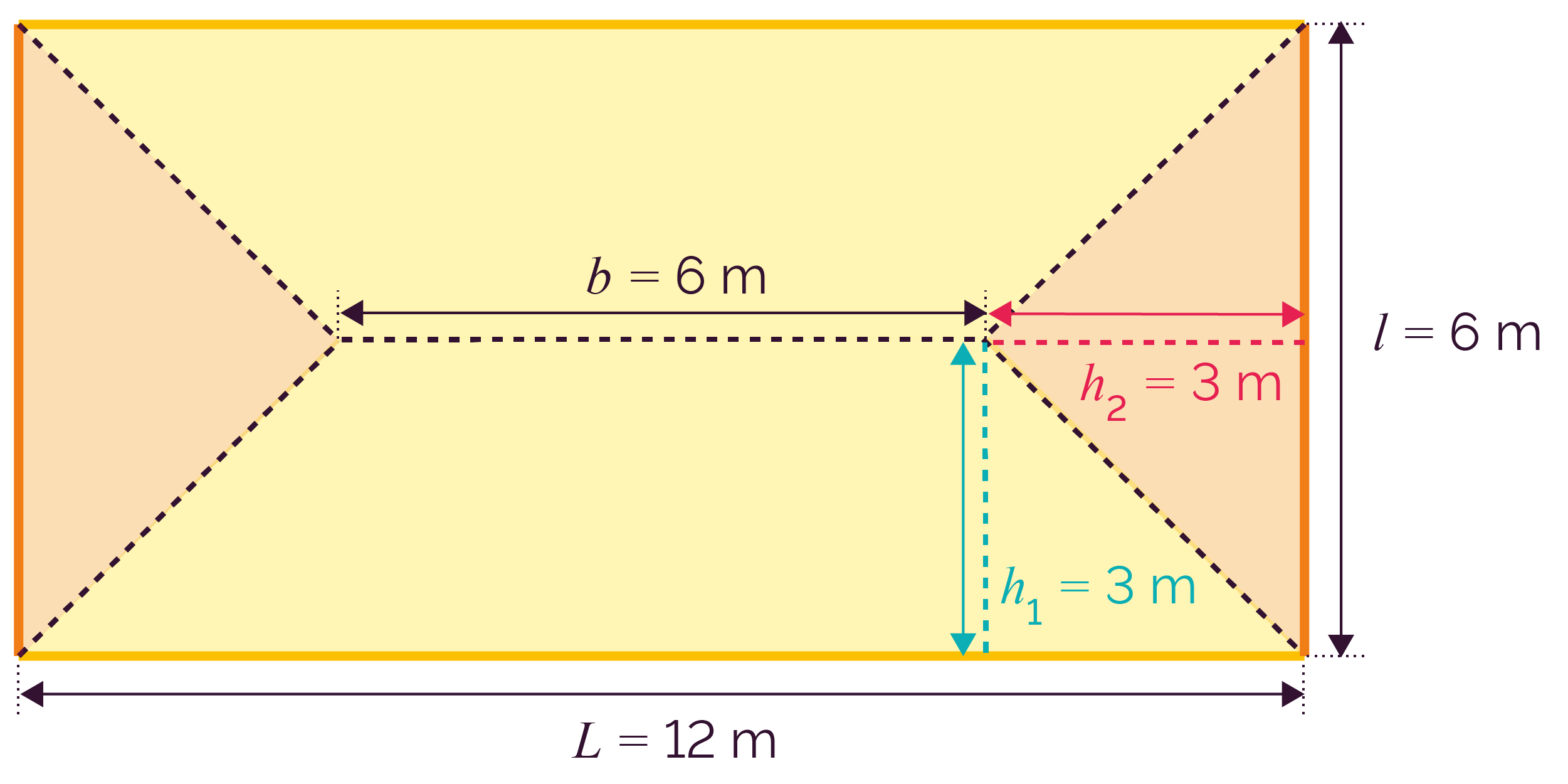
On calcule ensuite les aires des zones d’influence :

• pour un mur de façade (plus grande longueur), dont la zone d’influence est un trapèze :

  A_{ZI façade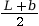}=  × h₁

  A_{ZI façade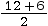} =  × 3 = 9 × 3 = 27 m²

• pour un mur de pignon, dont la zone d’influence est un triangle :

  A_{ZI pignon} = 

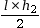
  A_{ZI pignon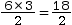} =  = 9 m²

Chaque mur reçoit donc le poids suivant.

• Pour un mur de façade :

  %_{ZI façade}= 

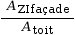
  %_{ZI façade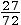} =  = 0,375 = 37,5 % du poids de ce qui se trouve au-dessus de lui.

• Pour un mur de pignon :

  %_{ZI pignon} = 

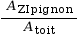
  %_{ZI pignon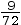} =  = 0,125 = 12,5 % du poids de ce qui se trouve au-dessus de lui.

Au niveau des aires des sections des murs, on a :

• pour un mur de façade : A_façade= L × l = 12 × 0,2 = 2,4 m²
• pour un mur de pignon : A_pignon = L × l = 6 × 0,2 = 1,2 m²

La contrainte σ dans ces murs, qui est due aux charges du toit et de la neige, sera donc :

• pour un mur de façade :

  σ_t+n/façade= 

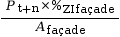
  σ_t+n/façade = 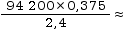 14 700 Pa

• pour un mur de pignon :

  σ_t+n/pignon = 

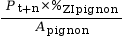
  σ_t+n/pignon = 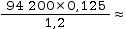 9810 Pa

Chaque mur doit résister :

• à une partie de la contrainte due au toit et de la neige σ_t+n/façade ou σ_t+n/pignon ;
• à la charge permanente G_mur due au poids des parpaings.

Comme les murs ont la même hauteur et sont faits du même matériau, la charge G_mur est la même pour les quatre murs (façade et pignon).

Elle peut se calculer en divisant le poids d’un mur par sa section.

Calcul de la masse M_façade d’un mur en parpaing (ici la façade)

M_façade= V_façade × ρ_parpaing

M_façade= L_façade × l_façade × h_façade × ρ_parpaing

M_façade= 12 × 0,2 × 2,4 × 1750 ≈ 10 100 kg

Calcul du poids P_façade du mur

P_façade= M × g

P_façade ≈ 10 100 × 9,81 ≈ 99 000 N

Calcul de la charge G_mur du mur

G_mur= 

G_mur =  ≈ 41 300 Pa

On a donc les contraintes globales σ suivantes pour les murs.

• Pour un mur de façade :

  σ_façade= σ_t+n/façade+ G_mur

  σ_façade= 14 700 + 41 300 ≈ 56 000 Pa ≈ 56 kPa

• Pour un mur de pignon :

  σ_pignon = σ_t+n/pignon + G_mur

  σ_pignon = 9810 + 41 300 ≈ 51 100 Pa ≈ 51,1 kPa

En tenant compte du coefficient de sécurité K = 1,5, on a :

• pour un mur de façade :

  σ_façade × K = 56 × 1,5 ≈ 84 kPa  40 MPa

• pour un mur de pignon :

  σ_pignon × K = 51,1 × 1,5 ≈ 76,7 kPa  40 MPa

Les deux murs sont donc largement assez résistants.

La surface de la dalle vaut A_dalle= 14 × 8 = 112 m².

La dalle de fondation doit résister :

• au poids du toit et de la neige, qui vaut P_t+n= 93 800 N, qui produira une contrainte σ_t+n/dalle ;
• au poids des quatre murs P_4murs, qui produiront une contrainte σ_4murs/dalle ;
• à la charge d’exploitation de la maison Q = 200 N·m^–2 ;
• à sa propre charge permanente due au poids de la dalle P_dalle, qui produira une charge G_dalle.

Calcul de la contrainte σ_t+n/dalle

σ_t+n/dalle =  = 841 Pa

Calcul de la contrainte σ_4murs/dalle

Le poids des 4 murs (qui sont en parpaing) vaut :

P_4murs= M_4murs × g

P_4murs = V_4murs × ρ_parpaing × g

P_4murs = L_4murs × l_4murs × h_4murs × ρ_parpaing × g

P_4murs = (2 × L_façade + 2 × l_pignon) × l_4murs × h_4murs × ρ_parpaing × g

P_4murs ≈ (2 × 12 + 2 × 6) × 0,2 × 2,4 × 1750 × 9,81

P_4murs ≈ 297 000 N

On peut ainsi calculer σ_4murs/dalle :

σ_4murs/dalle =  ≈ 2650 Pa

Calcul de la charge G_dalle

G_dalle = 

G_dalle =   13 600 Pa

En sommant les différentes contraintes et charges subies par la dalle, on obtient une contrainte dans la dalle de :

σ_dalle = σ_t+n/dalle + σ_4murs/dalle + Q + G_dalle

σ_dalle = 841 + 2650 + 200 + 13 600 ≈ 17 300 Pa ≈ 17,3 kPa

En tenant compte du coefficient de sécurité K = 1,5, on a :

σ_dalle × K = 17,3 × 1,5 ≈ 26 kPa  15 MPa

La dalle est donc largement assez résistante.

La pression exercée par la structure sur le sol est égale à la contrainte dans la dalle : p_{structure/sol}= σ_dalle.

D’après les données, la résistance à l’enfoncement dans le sol est :

 = 0,3 MPa = 300 kPa.

p_{structure/sol} × K = 17,3 × 1,5 ≈ 26 kPa

26 kPa < 300 kPa.

La maison ne s'enfoncera donc pas dans le sol.