La mécanique du point et les équations horaires
- Modéliser un objet selon la mécanique du point.
- Connaitre les équations horaires.
- Résoudre un problème de mécanique du point à l’aide des équations horaires.
- La mécanique du point propose de modéliser l’objet étudié par un point, plutôt que par un solide.
- Un point qui représente un objet est caractérisé par une masse et par un vecteur position. L’étude de l’évolution de la position du point se fait grâce au vecteur vitesse et au vecteur accélération.
- Les équations horaires permettent de
déterminer la position et la vitesse en fonction du
temps.
- Position :
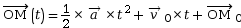
- Vitesse :
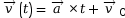
- Position :
- Connaitre les lois du mouvement de Newton et ce qu’est un référentiel galiléen.
- Savoir utiliser un repère orthonormé et des vecteurs.
- Connaitre les primitives usuelles.
- Connaitre les notions de mouvement, vitesse et accélération.
La mécanique du point est plus adaptée que la mécanique des solides pour résoudre certains problèmes.
La mécanique du point permet aussi d'assez bien modéliser les objets de petites dimensions par rapport à leur environnement.
Le point choisi pour représenter l'objet est souvent son centre de gravité. Ce point est étudié dans un référentiel galiléen et est associé à un repère tridimensionnel (Oxyz), orthogonal et orthonormé.
- Un référentiel galiléen est un référentiel dans lequel tous les objets libres (qui ne subissent aucune force) sont soit immobiles, soit en mouvement de translation rectiligne uniforme.
- Un repère est orthogonal si ses axes sont perpendiculaires les uns aux autres.
- Un repère est orthonormé si les graduations sur chacun de ses axes ont la même norme, c’est-à-dire la même longueur.
En mécanique du point, le point qui modélise l’objet étudié est caractérisé par une masse m, en kilogramme (kg).
Le point est aussi caractérisé par un vecteur position.
Si on nomme le point par la lettre M, avec O l'origine du repère,
son vecteur position est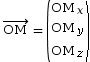 
.
L'unité des composantes d'OM est le
mètre (m).
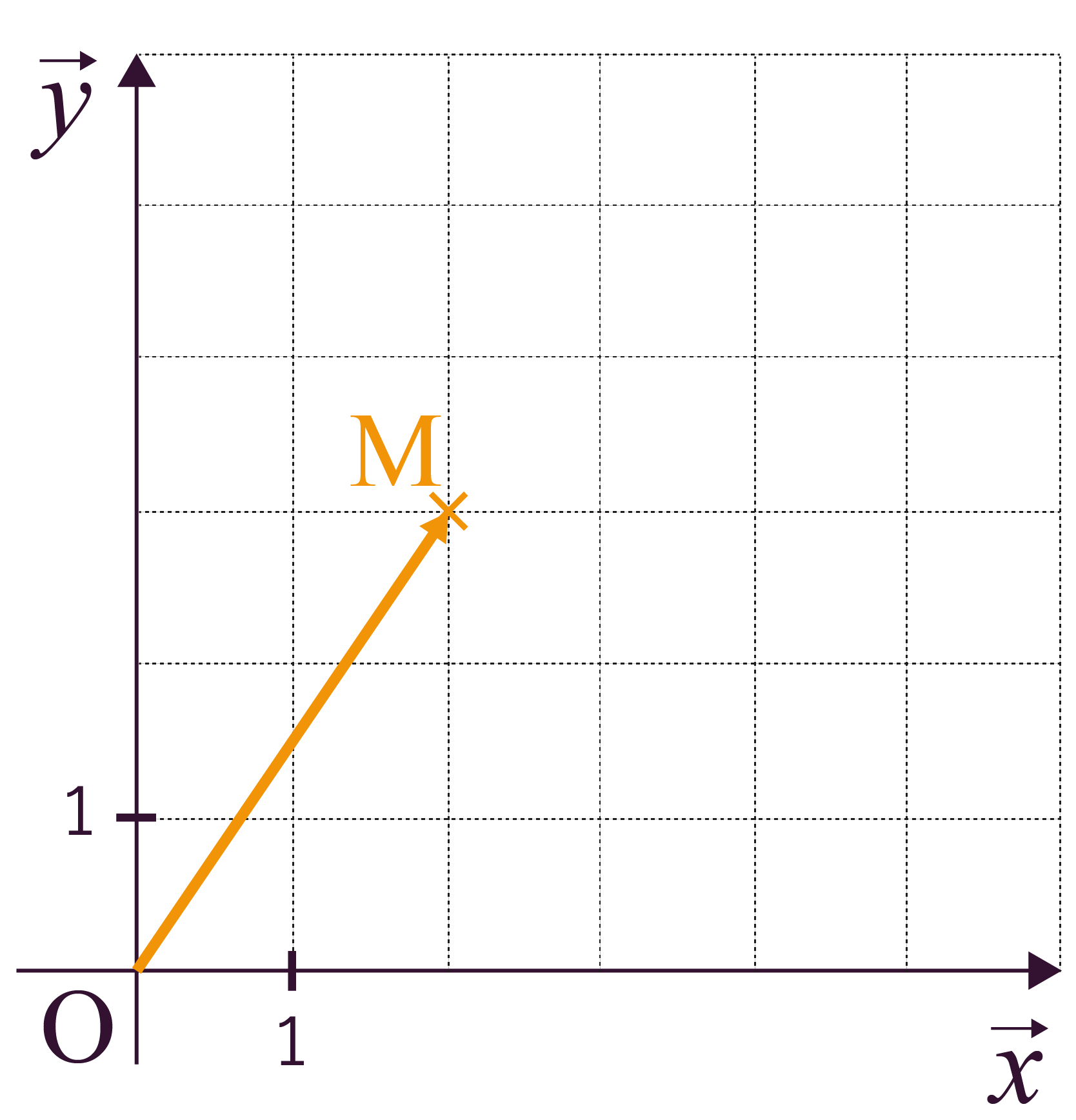
Dans le repère orthonormé (Oxy) ci-dessus,
l’objet modélisé par le point
M a pour
coordonnées (2 ; 3).
Son vecteur position est 
.
Le point est également associé à
un vecteur vitesse,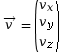 
.
L'unité des composantes de 
est le mètre par seconde
(m·s–1).
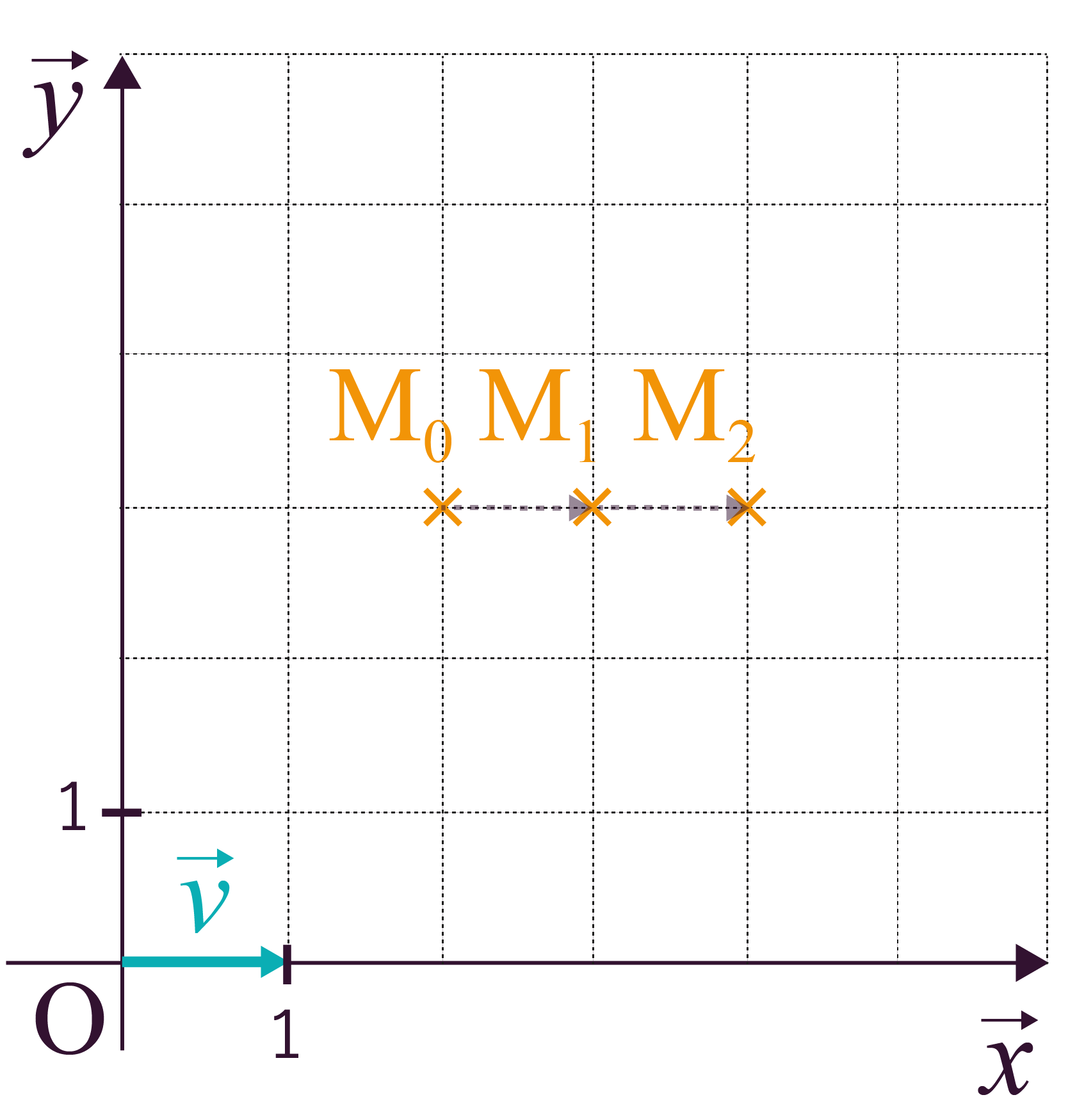
Dans le repère orthonormé (Oxy) ci-dessus,
l’objet modélisé par le point
M a pour vecteur
position initial 
.
On sait aussi que son vecteur vitesse est 
.
Le point M va
donc se déplacer, suivant le vecteur
, pour chaque unité
de temps. On obtient ainsi 
, puis 
, etc.
Si la vitesse est constante, l’objet est en mouvement de translation rectiligne uniforme.
Le point possède de plus un vecteur
accélération,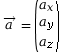 
.
L'unité des composantes de 
est le mètre par seconde
au carré
(m·s–2).
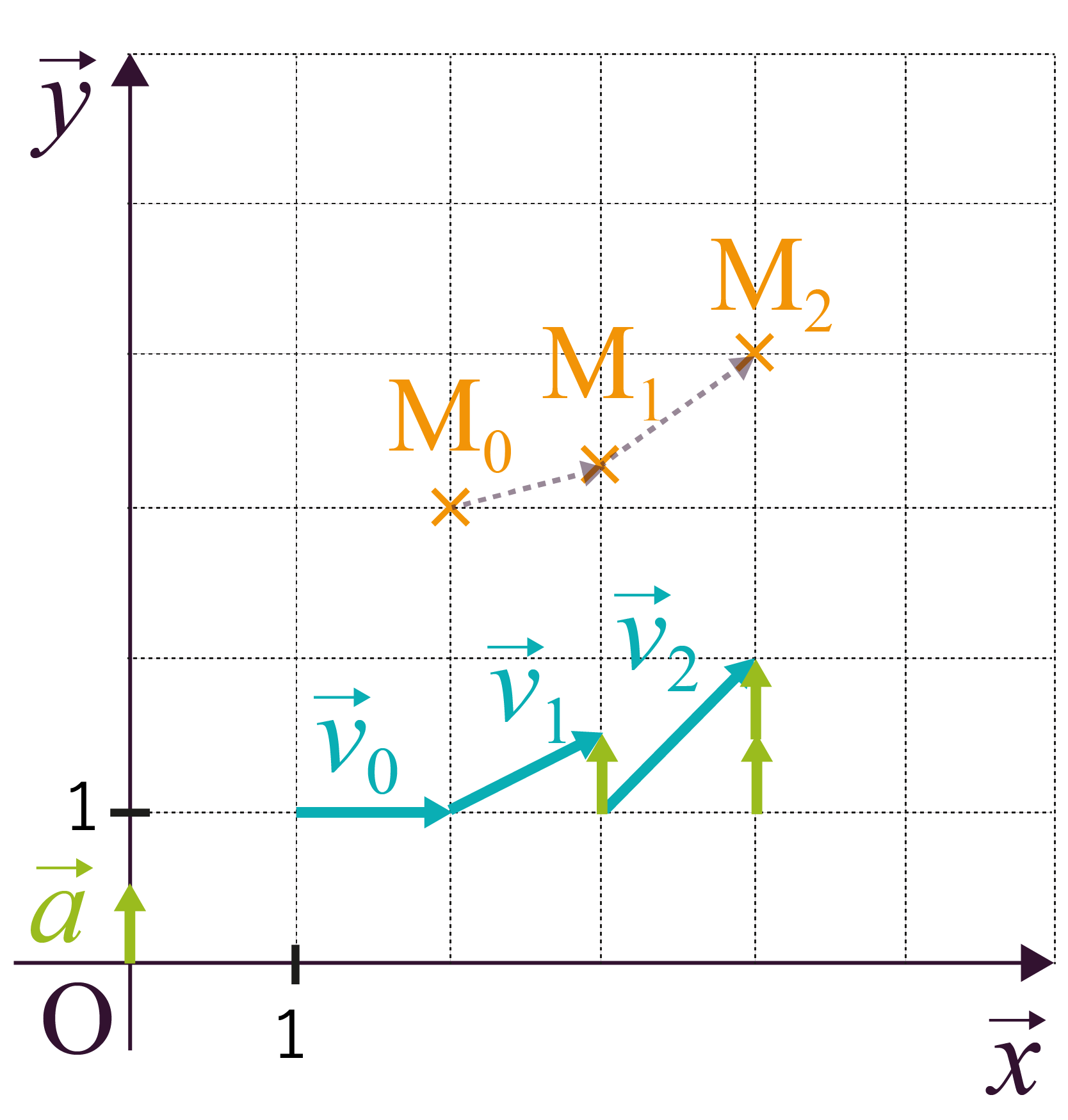
Dans le repère orthonormé (Oxy) ci-dessus,
l’objet modélisé par le point
M a pour vecteur
position initial 
.
On sait aussi que son vecteur vitesse vaut
initialement 
et que son vecteur
accélération vaut 
.
Le vecteur vitesse va donc être modifié,
suivant le vecteur 
, pour chaque unité
de temps. On obtient ainsi 
, puis 
, etc.
La détermination exacte du vecteur position
sera présentée dans la suite de la
fiche, mais on peut voir l’évolution du
vecteur position, qui suit celle du vecteur vitesse,
ce qui donne 
, puis 
, etc.
Si la vitesse et l’accélération sont colinéaires, c’est-à-dire qu’ils ont la même direction, l’objet est en mouvement de translation rectiligne, mais pas uniforme.
Enfin, on pourra tracer la trajectoire du point, et donc de l’objet.
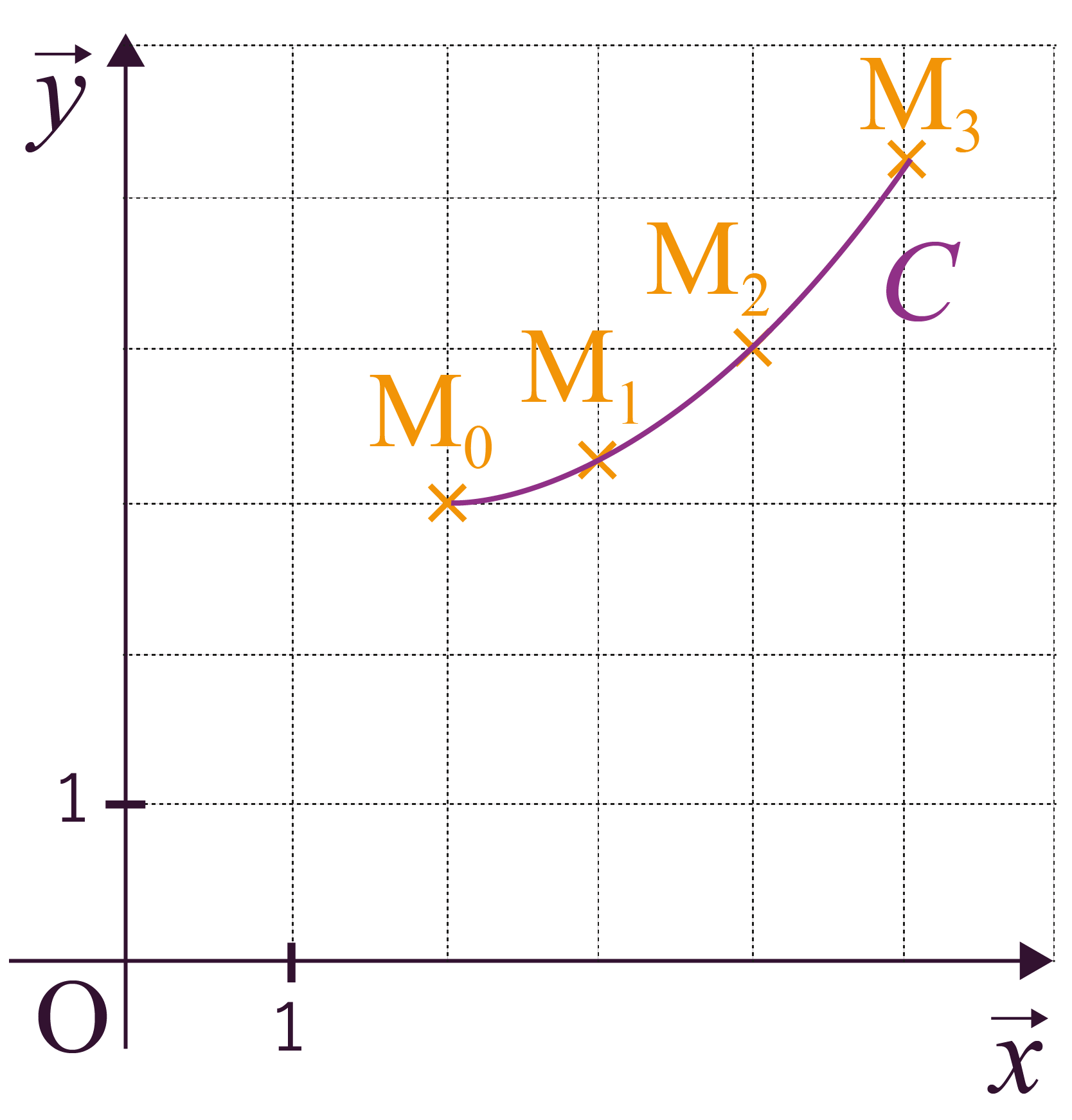
Dans le repère orthonormé
(Oxy)
ci-dessus, le point M va successivement occuper
les positions M0, M1, M2 et M3.
La trajectoire de l’objet peut donc être
représentée par la courbe C.
Si la vitesse et/ou l'accélération ne sont pas toutes les deux nulles, alors la position de l’objet va évoluer au cours du temps.
Pour représenter cette évolution, on note :
- le vecteur position initial
;
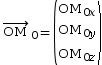- la fonction qui représente le
vecteur
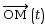en fonction du temps 
.
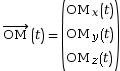De même, si l'accélération n'est pas nulle, alors la vitesse de l’objet va évoluer au cours du temps.
Pour représenter cette évolution, on note :
- le vecteur vitesse initial
;
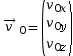- la fonction qui représente le vecteur
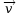en fonction du
temps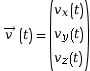 
.
- Dans les problèmes étudiés au lycée, l'accélération est constante.
- Quand l’accélération
n’est pas donnée dans
l’énoncé, on peut utiliser le
principe fondamentale de la dynamique (PFD) pour la
déterminer. On se sert alors de la masse de
l’objet pour résoudre
l’équation
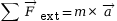, qui devient 
.
.
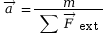Si f(t) = 
alors sa primitive en fonction
du temps vaut :
F(t) = 
.
En prenant 
comme constante
d'intégration, on obtient
l’équation suivante.
|
|
avec :
|
le vecteur
vitesse du point à l’instant
l’accélération du point,
en m
le vecteur
vitesse initial, en m
.
Si f(t) = 
, alors sa primitive en fonction
du temps vaut :
F(t) = 
En prenant 
comme constante d'intégration, on
obtient l’équation suivante.
|
|
avec :
|
le vecteur position du point
à l’instant 
l’accélération du point,
en m
le vecteur
vitesse initial, en m
le vecteur position initial du
point, en m
Voici un exemple complet d’utilisation des équations horaires pour résoudre un problème de mécanique.
On étudie la chute d’un objet, à 7 m de hauteur et lancé avec une vitesse horizontale de 3 m·s–1.
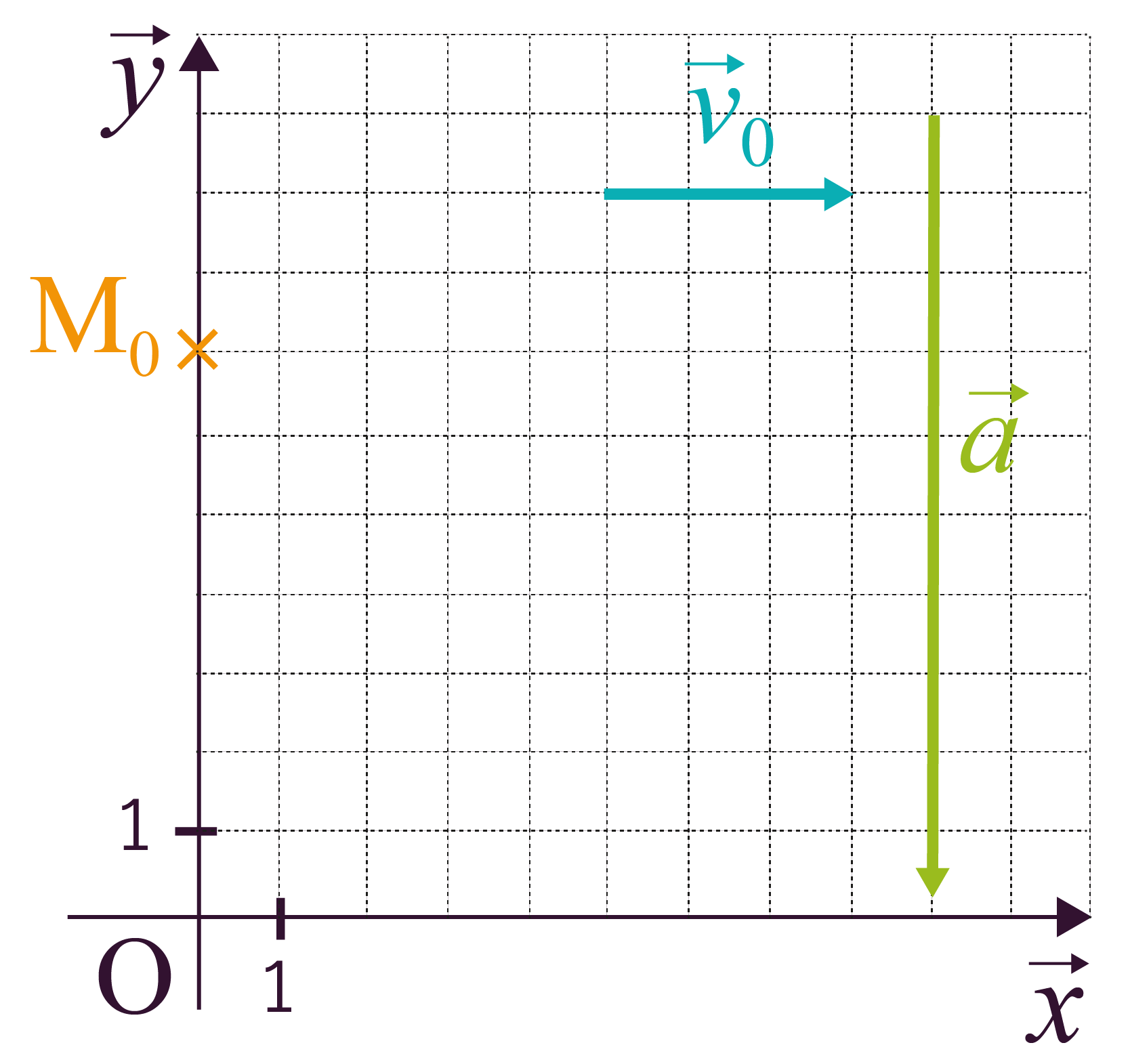
L’objet est modélisé par un point M. On est dans le cas d’un problème plan, de plan (Oxy). L’axe des abscisses (Ox) représente le sol. Enfin, on néglige le frottement de l’air et on considère que l’objet n’est soumis qu’à la force de pesanteur.
Un problème plan est une situation dans laquelle les mouvements n'ont lieu que dans un plan de l’espace, on peut alors ignorer la troisième dimension.
On détermine graphiquement les caractéristiques du point M.
- Vecteur position initial
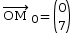
- Vecteur vitesse initial
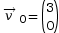
- Vecteur accélération
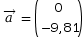
La valeur –9,81 vient de l’accélération de pesanteur à la surface de la Terre : g = 9,81 m·s–2.
L’application des équations horaires permet de connaitre la vitesse et la position du point M au cours du temps.
Cela donne, sur l’axe 
:
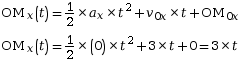
Cela donne, sur l’axe 
:
.
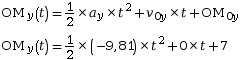
Cela revient ici à résoudre
l’équation 
.
Il y a mathématiquement deux solutions
et 
.
Physiquement, on s’intéresse à un événement qui se déroule après t = 0 s. On prend donc la solution positive : l’objet touche le sol au bout de 1,2 s.
Lorsque l’objet touche le sol (en t = 1,2 s) sa vitesse sera alors de :
-
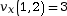m·s–1
sur l’axe 
;
-
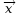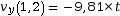
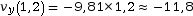m·s–1
sur l’axe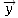 
.
Soit :
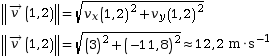
Pour connaitre la distance parcourue par l’objet,
on utilise l’équation horaire de la
position sur l’axe 
: 
.
À l’instant t = 1,2 s
où l’objet touche le sol, on a :
m.
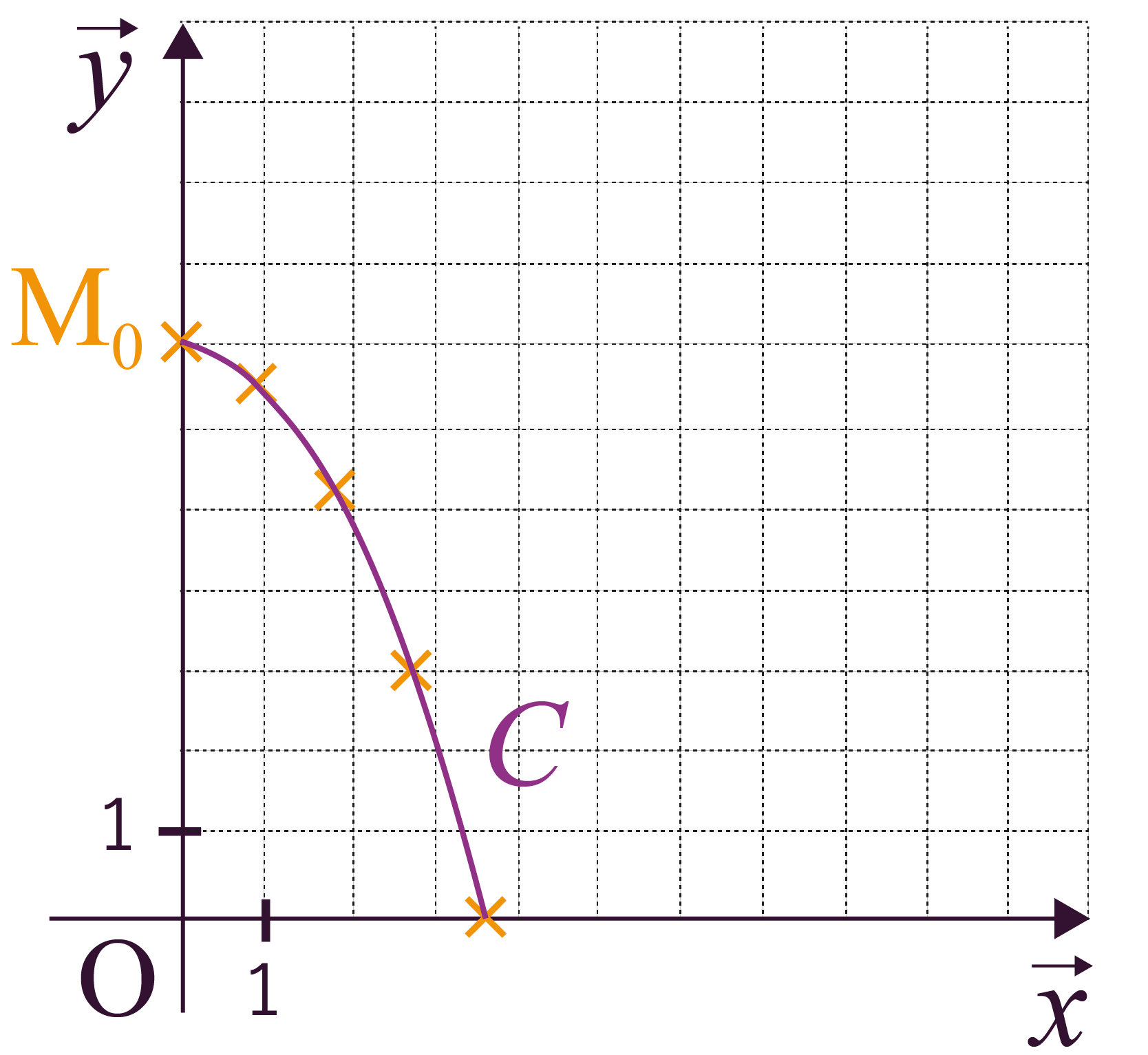
On calcule les coordonnées de quelques positions de M(t), dans l’intervalle {0 ; 1,2} de t.
On se sert des deux équations horaires de la position de M, trouvées précédemment :
| t | 0 | 0,3 | 0,6 | 0,9 | 1,2 |
| x | 0 | 0,9 | 1,8 | 2,7 | 3,6 |
| y | 7 | 6,6 | 5,2 | 3 | 0 |
On place ensuite les points trouvés dans le repère, puis on trace la courbe C qui représente la trajectoire de l’objet jusqu’à ce qu’il atteigne le sol.
Vous avez déjà mis une note à ce cours.
Découvrez les autres cours offerts par Maxicours !
Découvrez MaxicoursComment as-tu trouvé ce cours ?
Évalue ce cours !
Fiches de cours les plus recherchées
Des profs en ligne
- 6 j/7 de 17 h à 20 h
- Par chat, audio, vidéo
- Sur les matières principales
Des ressources riches
- Fiches, vidéos de cours
- Exercices & corrigés
- Modules de révisions Bac et Brevet
Des outils ludiques
- Coach virtuel
- Quiz interactifs
- Planning de révision
Des tableaux de bord
- Suivi de la progression
- Score d’assiduité
- Un compte Parent
Message envoyé
