Descente de charges : les structures porteuses
- Identifier les éléments d’une structure porteuse.
- Identifier les types de charges dans un bâtiment.
- Déterminer si un élément structural peut résister à une charge.
- La structure porteuse d'un bâtiment comprend l'ensemble des éléments qui lui permettent de supporter des charges.
- La descente de charges est l’étude du transfert des charges, du haut vers le bas, dans un bâtiment.
- La structure porteuse d’un bâtiment doit
supporter :
- des charges permanentes ;
- des surcharges d’exploitation ;
- des surcharges liées au climat et aux risques sismiques.
- La capacité d’un élément structural à résister à une charge se détermine en comparant la contrainte σ qu’il subit avec sa limite d’élasticité Rec.
Notions en résistance des matériaux
La structure porteuse est aussi nommée « ossature du bâtiment ». On l'oppose à l'enveloppe, qui comprend tous les éléments qui couvrent l'ossature.
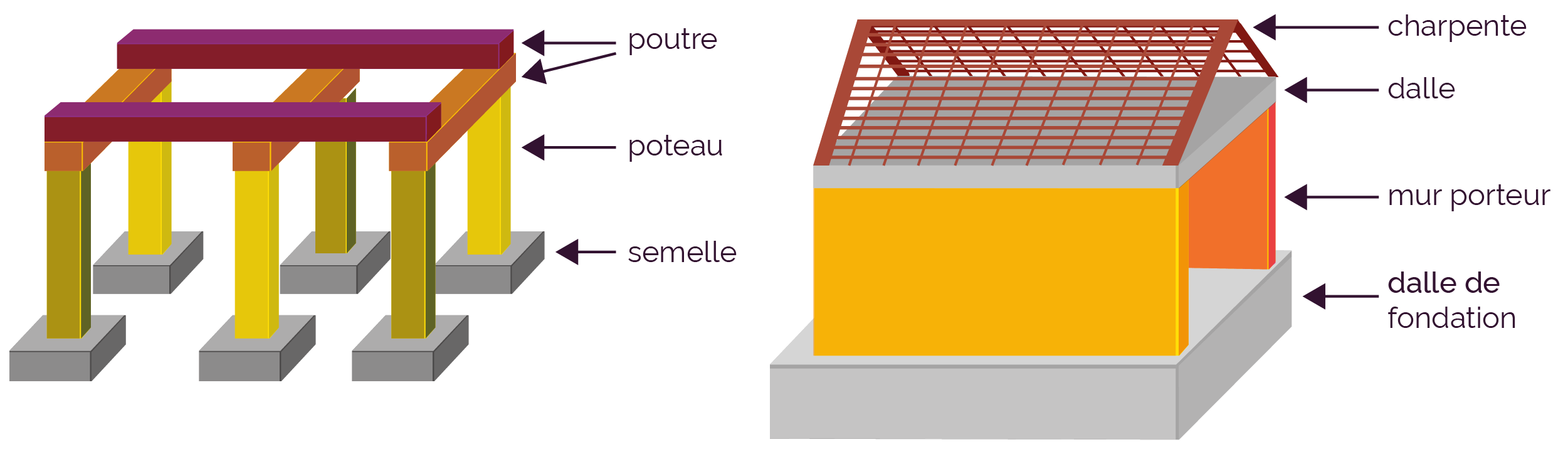
Une structure porteuse comporte plusieurs types d'éléments, dont notamment :
- des éléments verticaux : murs
porteurs, poteaux ;
Remarque
Un mur n’est pas forcément porteur, il y a aussi des murs qui servent juste à séparer des pièces. On les appelle cloisons de distribution. - des éléments horizontaux : dalles, poutres ;
- des éléments de fondation : dalle de fondation, semelles ;
- des éléments de charpente.
Chaque élément d'une structure porteuse a pour objectif :
- d’assurer la rigidité et la stabilité de l’ensemble ;
- de résister aux charges qui lui sont transmises par les éléments au-dessus de lui ;
- de transmettre les charges aux éléments qui sont en dessous de lui.
La réalisation d’une étude sur la descente de charges d’un bâtiment permet de dimensionner les éléments de sa structure porteuse. Elle permet de choisir les formes, épaisseurs et matériaux adaptés à chaque élément structural pour qu'il soit suffisamment rigide et résistant.
Un élément de la structure porteuse est en généralement soutenu par plusieurs autres éléments porteurs.
- Une dalle soutenue par quatre poutres.
- Une poutre soutenue par trois poteaux.
Cette zone dépend essentiellement de la géométrie des éléments supérieurs et inférieurs.
Voici quelques exemples courants de zones d’influence.
|
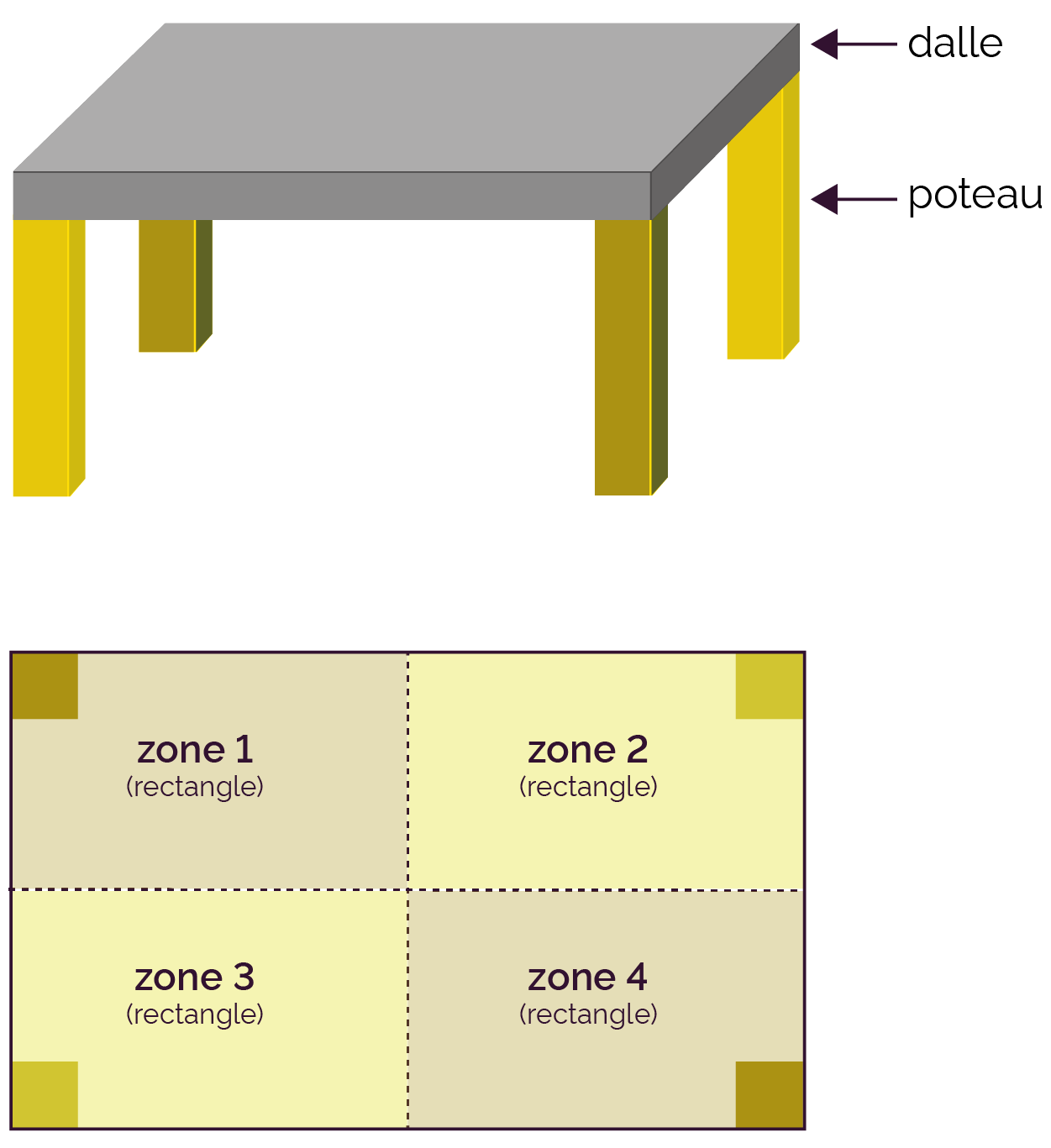
Les zones, et donc les charges, sont équitablement réparties entre les poteaux qui pourront avoir les mêmes dimensions. Les zones sont des rectangles dont l'aire est facilement calculable. |
|
|
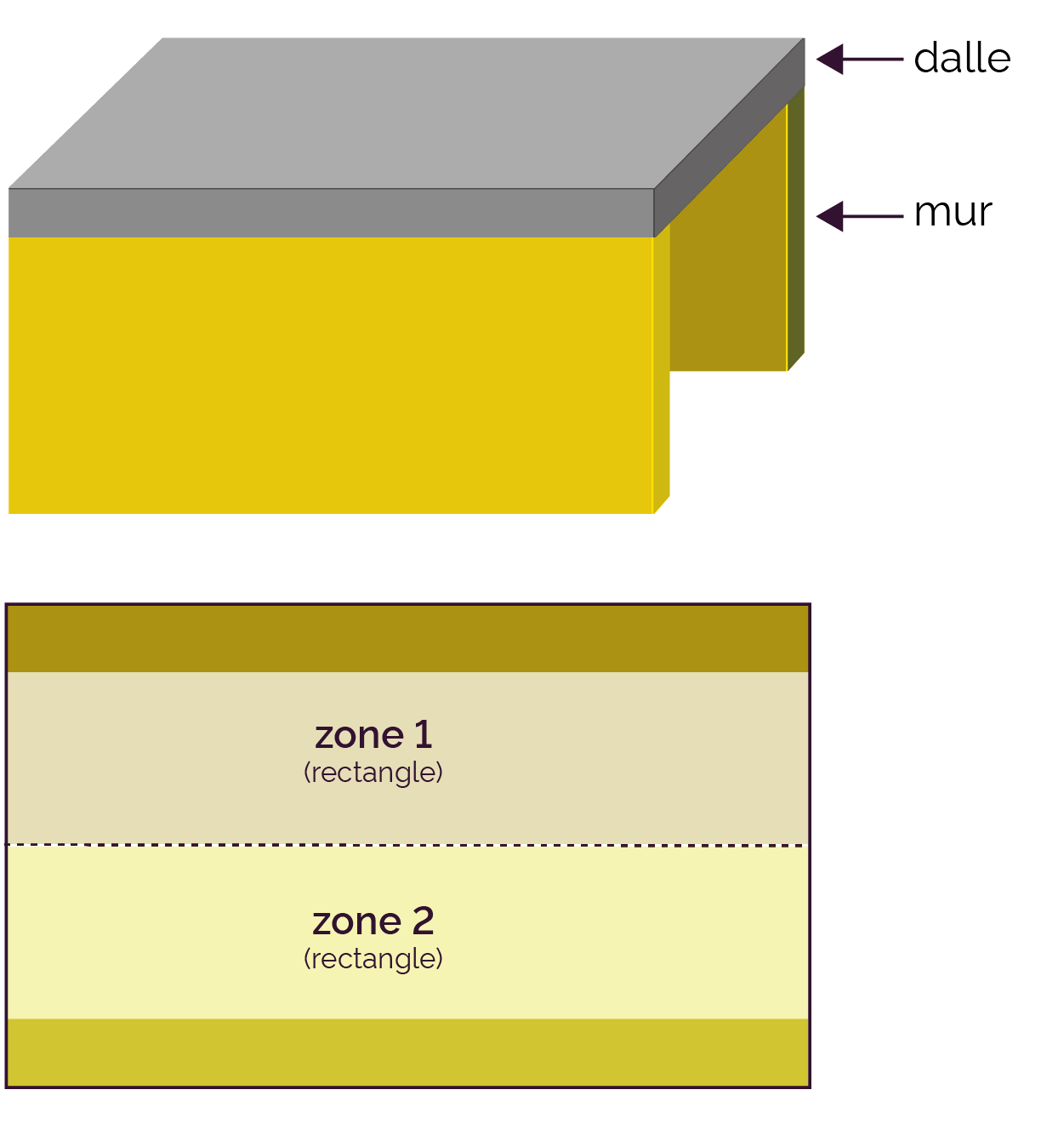
Les zones, et donc les charges, sont équitablement réparties entre les murs qui pourront avoir les mêmes dimensions. Les zones sont des rectangles dont l'aire est facilement calculable. |
|
|
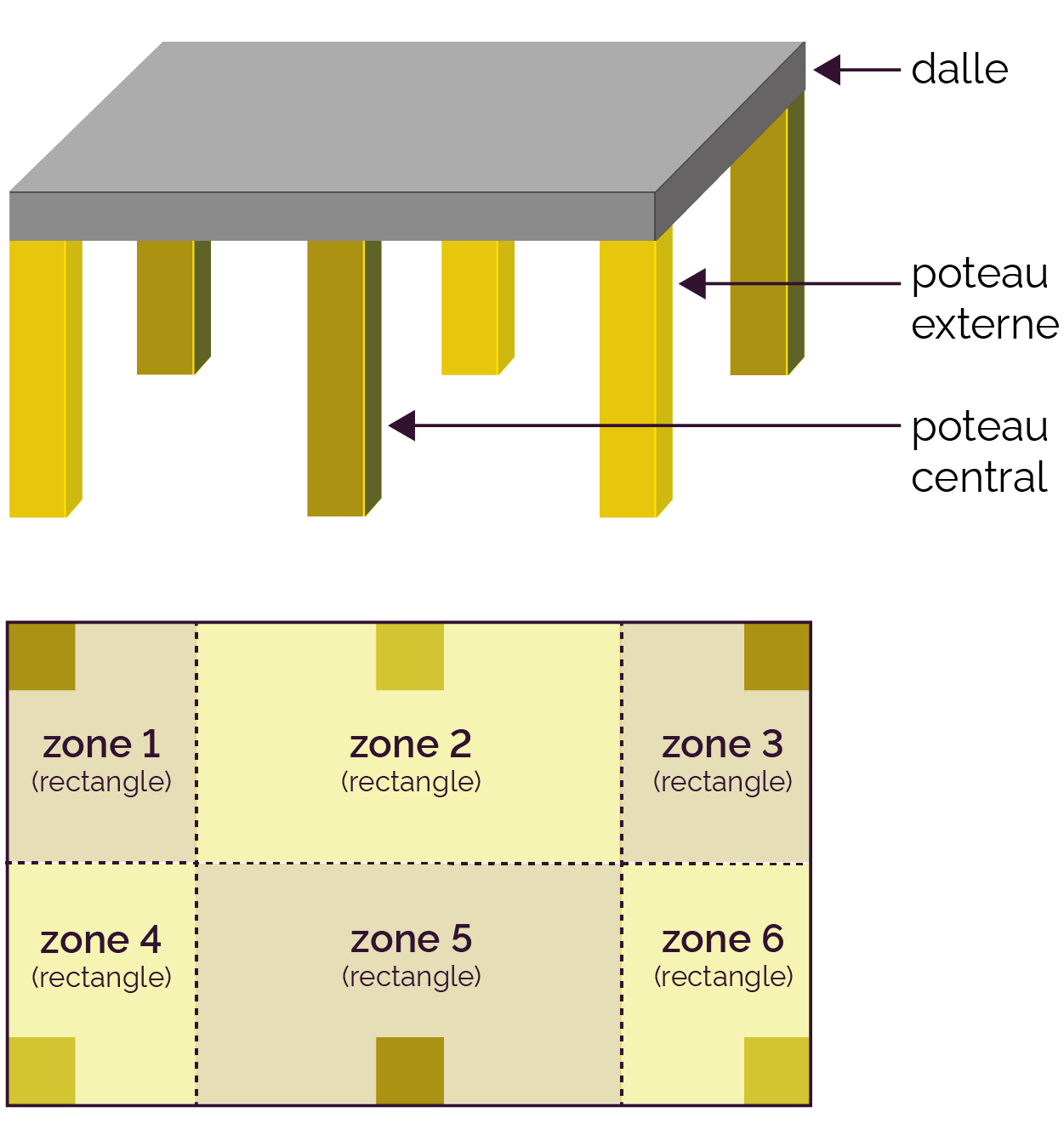
Les zones, et donc les charges, ne sont pas équitablement réparties entre les poteaux. Soit les poteaux centraux seront dimensionnés différemment des autres pour être plus résistants, soit tous les poteaux seront dimensionnés de la même manière, mais les poteaux externes seront alors surdimensionnés. Les zones sont des rectangles dont l'aire est facilement calculable. |
|
|
Les zones sont plus importantes sur les murs de façades (les murs les plus long) qui devront être dimensionnés pour être un peu plus résistants. La séparation entre les zones d’influence se fait en suivant une droite à 45°. |
|
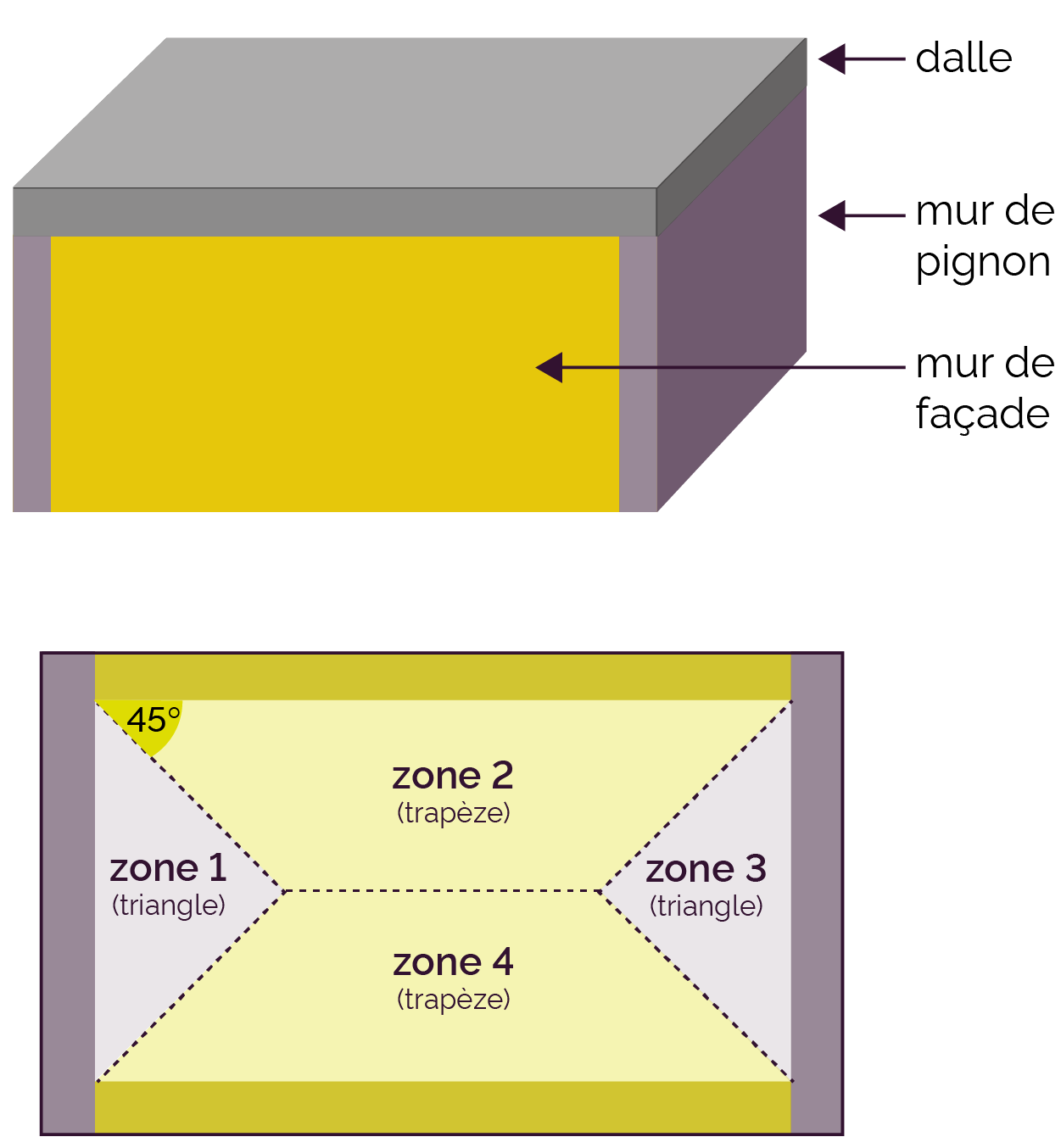
L'épaisseur des murs étant faible par rapport à la largeur du dalle, on peut faire une approximation quant à la forme des zones d'influence et considérer que ce sont des triangles et des trapèzes.
Ces éléments font partie :
- de la structure porteuse ;
- de l'enveloppe (isolation, cloison, couverture, etc.) ;
- des installations techniques (réseaux électrique, plomberie, etc.).
Comme leur nom l'indique, les charges permanentes doivent être supportées en continu par la structure porteuse du bâtiment.
« Pression » et « force surfacique » sont des termes équivalents, mais il est plus courant d’utiliser la force surfacique en construction.
Les charges permanentes d'une maison sont liées aux poids combinés de la charpente, des tuiles, des poutres, des murs, des différents revêtements pour sols et murs, de l'isolation, des menuiseries, du réseau électrique, du réseau d'eau et des fondations.
Les surcharges d'exploitation d'une maison comprennent le poids des personnes qui habitent la maison, les meubles, l’électroménager, etc.
Les surcharges d'exploitation sont liées à la fonction du bâtiment (habitation, commerce, industrie, etc.). Elles sont, contrairement aux charges permanentes, irrégulières et partiellement intermittentes.
Les surcharges d'exploitation, selon le type d'utilisation du bâtiment, sont décrites par la norme EN 1991 Eurocode 1.
D'autres surcharges doivent être prises en compte en fonction de la localisation géographique du bâtiment.
Notamment :
- les surcharges liées aux conditions climatiques, principalement le vent (notées W) et la neige (notée S) ;
- les surcharges liées aux risques sismiques (notée F).
Ces surcharges sont exprimées en newton par mètre carré (N·m–2) ou en Pascal (Pa).
La manière dont sont prises en compte des surcharges liées aux conditions climatiques et sismiques sont décrites par la norme EN 1991 Eurocode 1.
Dans un élément structural (mur, poteaux, etc.) soumis à un effort de compression, la contrainte subie se note σ et se calcule avec la formule suivante.
|
avec :
|
- On prend la section normale (perpendiculaire) à la force.
- Si la géométrie de l’élément fait que la section n’a pas toujours la même surface, on prend la plus petite section possible.
Le poteau ci-dessus est comprimé entre le sol
et des éléments de construction
situés au-dessus de lui.
Il en résulte une force de compression de
23 000 N.
Sa section, perpendiculaire à la force, est un
rectangle de 16 cm par 12 cm, soit une surface
de A = 0,12 × 0,16 =
0,0192 m2.
On obtient donc une contrainte dans le poteau
de :
1 200 000 Pa 
1,2 MPa.
Chaque matériau possède une caractéristique nommée limite d’élasticité.
Lors du dimensionnement d’un élément structural, il faut veiller à ce que cette limite ne soit pas dépassée.
- La limite d’élasticité des matériaux courants est toujours fournie dans les énoncés.
- La limite d’élasticité est différente selon le type d’effort subi (compression, traction, flexion, etc.). Dans ce cours, on ne s’occupe que de la compression.
La limité d’élasticité en compression du béton est Rec = 15 MPa. Le poteau de l’exemple précédent est donc suffisamment résistant si il est fabriqué en béton.
Cela signifie qu’il faut vérifier que l’inégalité σ < Rec est bien respectée pour chaque élément.
Si ce n’est pas le cas, on doit :
- changer les dimensions de l’élément pour agrandir sa section ;
- modifier la répartition des forces en agissant sur les zones d’influence ;
- changer de matériau et en prendre un plus résistant.
Cependant, on utilise rarement l’inégalité précédente telle quelle. On préfère lui ajouter un coefficient de sécurité K, supérieur à 1, pour augmenter virtuellement la contrainte subie par l’élément structural.
Les coefficients de sécurité, selon le type d’élément structural et la situation, sont décrits par la norme EN 1991 Eurocode 1.
Si on reprend l’exemple précédent, le poteau subit une contrainte σ
1,2 MPa et possède une limite
d’élasticité Rec = 15 MPa.
1,8 < 15 qui est
vérifiée. Le dimensionnement du poteau
est donc satisfaisant.
On calcule alors la pression exercée par un élément sur le sol avec la formule suivante.
|
avec :
|
la pression exercée par
un élément sur le sol, en
NOn peut de nouveau appliquer un coefficient de sécurité K. On compare ensuite la pression exercée par l’élément sur le sol avec la résistance à l’enfoncement du sol, Renf, qui s’exprime en Pascal (Pa).
.
Si on reprend l’exemple précédent, le poteau supporte un poids équivalent à 23 000 N et l’aire de sa surface en contact avec le sol est A = 0,0192 m2.
On obtient donc une pression sur le sol
1 200 000 Pa 
1,2 MPa. Si le poteau repose sur un sol dont la résistance à l’enfoncement vaut Renf = 0,3 MPa, et qu’on utilise un coefficient de sécurité, K = 1,3, alors l’inégalité 1,3 × 1,2 < 0,3
1,56 <
0,3 n’est pas
vérifiée. On en déduit que le poteau s’enfonce dans le sol. Il faut donc augmenter la section en contact avec le sol en élargissant la base du poteau.
- Une charge, une contrainte et une pression représentent le même phénomène physique : une force qui s’applique sur une surface. C’est pour cela qu’elles ont la même unité, le Pa = N·m–2, et qu’on peut les additionner et les comparer avec des inégalités.
- Les charges sont notées avec une lettre
majuscule :
G (charge permanente), Q (surcharge d’exploitation), S (surcharge due à la neige) et W (surcharge due au vent). - Les contraintes à l’intérieur d’un matériau sont notées avec la lettre grecque sigma σ.
- Pour la pression sur le sol, on utilise la lettre minuscule p.
Vous avez déjà mis une note à ce cours.
Découvrez les autres cours offerts par Maxicours !
Découvrez MaxicoursComment as-tu trouvé ce cours ?
Évalue ce cours !
Fiches de cours les plus recherchées
Des profs en ligne
- 6 j/7 de 17 h à 20 h
- Par chat, audio, vidéo
- Sur les matières principales
Des ressources riches
- Fiches, vidéos de cours
- Exercices & corrigés
- Modules de révisions Bac et Brevet
Des outils ludiques
- Coach virtuel
- Quiz interactifs
- Planning de révision
Des tableaux de bord
- Suivi de la progression
- Score d’assiduité
- Un compte Parent
Message envoyé
