Fiche de cours

Les indicateurs d'une série statistique

Lycée > Seconde > Mathématiques > Les indicateurs d'une série statistique

Fiche de cours
Quiz et exercices
Vidéos et podcasts

Objectifs

Calculer une moyenne pondérée.
Déterminer une médiane.
Déterminer les quartiles et l’écart interquartile d’une série statistique.
Déterminer une étendue.
Déterminer un écart-type.

Points clés

La moyenne pondérée d’une série statistique s’obtient en faisant le calcul suivant : .
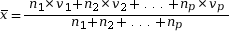La médiane d’une série statistique est le nombre qui partage cette série en deux groupes de même effectif :
- le groupe constitué des valeurs inférieures ou égales à la médiane ;
- le groupe constitué des valeurs supérieures ou égales à la médiane.
Les valeurs d’une série statistique étant rangées par ordre croissant :
- le premier quartile, généralement noté Q₁, est la plus petite valeur de la série pour laquelle au moins un quart des valeurs lui sont inférieures ou égales ;
- le troisième quartile, généralement noté Q₃, est la plus petite valeur de la série pour laquelle au moins trois-quarts des valeurs lui sont inférieures ou égales.
L’étendue d’une série statistique est l’écart entre la plus grande et la plus petite valeur du caractère.
L’écart interquartile est égal à Q₃ – Q₁.
Cet indicateur permet de mesurer la dispersion des valeurs de la série statistique autour de sa moyenne. Plus il est grand, plus les valeurs sont dispersées.
Si on connait la moyenne d’une série statistique, on peut calculer sa variance 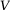par la formule :

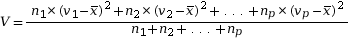
L’écart-type noté vaut .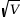
Il permet de mesurer la dispersion des valeurs de la série statistique autour de sa moyenne. Plus il est grand, plus les valeurs sont dispersées.
Contrairement à la médiane et à l’écart interquartile, la moyenne et l’écart-type sont très sensibles aux valeurs extrêmes d’une série statistique.
Ainsi, lorsque l’on doit comparer deux séries, on commence souvent par observer l’effectif des valeurs extrêmes.
- Si les valeurs extrêmes ont un effectif important, il est préférable de comparer les séries à l’aide de la médiane et de l’écart interquartile.
- Sinon, on utilisera plutôt la moyenne et l’écart-type.

1. Les indicateurs de tendance centrale

a. Moyenne et moyenne pondérée

Rappel
On parle de moyenne lorsque la série statistique est donnée sous la forme d’une suite de nombres. La moyenne d’une série statistique est égale au quotient de la somme de toutes les valeurs de cette série par l’effectif total. Elle est souvent notée

Exemple
À un contrôle de mathématiques, les 10 notes suivantes ont été obtenues :
{ 9 ; 12 ; 8 ; 7 ; 17 ; 12 ; 5 ; 10 ; 20 ; 15 }.

À ce contrôle, la moyenne de la classe est donc de 11,5.

On parle de moyenne pondérée lorsque la série statistique est donnée sous forme d’un tableau des effectifs.

Valeur	v₁	v₂	...	v_p
Effectif	n₁	n₂	...	n_p

La moyenne pondérée d’une série statistique s’obtient en faisant le calcul suivant :

Exemple
Le tableau suivant donne le relevé des âges des élèves d’un groupe :

Âge en années	14	15	16	17
Effectif	1	12	15	2

.
L’âge moyen des élèves de ce groupe est de 15,6 ans.

b. La médiane

La médiane d’une série statistique est le nombre qui partage cette série en deux groupes de même effectif :

le groupe constitué des valeurs inférieures ou égales à la médiane ;
le groupe constitué des valeurs supérieures ou égales à la médiane.

Méthode

Pour déterminer la médiane d’une série statistique, il faut commencer par classer les valeurs de la série dans l'ordre croissant. Deux cas sont alors possibles :

si est impair, on prend pour médiane la 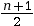ème valeur ;
si est pair, on prend pour médiane la moyenne entre la 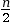ème et la 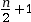ème valeur ;

Exemple 1
Les 9 notes obtenues à un contrôle sont les suivantes :
{ 10 ; 4 ; 7 ; 12 ; 5 ; 7 ; 8 ; 14 ; 15 }.
On commence par classer ces notes dans l’ordre croissant, ce qui donne :
{ 4 ; 5 ; 7 ; 7 ; 8 ; 10 ; 12 ; 14 ; 15 }.
Le nombre de notes, 9, étant impair, on prend pour médiane la note qui est en 9 + 12 = 5^e position. C'est-à-dire 8.

Exemple 2
Dans un groupe de 8 personnes, on relève par ordre croissant la taille de chaque personne. On obtient les valeurs suivantes en cm :
{ 160 ; 165 ; 167 ; 170 ; 176 ; 180 ; 182 ; 185 }.
Le nombre de personnes, 8, étant pair, on prend pour médiane la moyenne entre la 4^e note (c'est-à-dire 170) et la 5^e note (c'est-à-dire 176). La médiane vaut donc 173.

c. Les quartiles

Les valeurs d’une série statistique étant rangées par ordre croissant :

le premier quartile, généralement noté Q₁, est la plus petite valeur de la série pour laquelle au moins un quart des valeurs lui sont inférieures ou égales ;
le troisième quartile, généralement noté Q₃, est la plus petite valeur de la série pour laquelle au moins trois-quarts des valeurs lui sont inférieures ou égales.

Méthode pour déterminer Q₁

Comme Q₁ est la plus petite valeur de la série pour laquelle au moins un quart des valeurs lui sont inférieures ou égales, on prend le premier entier qui est supérieur ou égal à de l'effectif.

Méthode pour déterminer Q₃

Comme Q₃ est la plus petite valeur de la série pour laquelle au moins trois-quarts des valeurs lui sont inférieures ou égales, on prend le premier entier qui est supérieur ou égal à de l’effectif.

Exemple
En cours d’EPS, on a relevé les lancers de javelot d’une classe de 30 élèves. Le tableau suivant rassemble les résultats de la classe. Déterminer Q₁ et Q₃.

Longueur en m	38	39	40	41	43	45
Effectif	4	7	10	5	2	2

L’effectif total de cette série vaut 4 + 7 + 10 + 5 + 2 + 2 = 30.

Au moins un quart des valeurs de la série doivent être inférieures ou égales à Q₁. On calcule donc 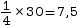. Q₁ correspond à la 8^e valeur de la série classée dans l’ordre croissant, soit Q₁= 39 m.
Au moins trois-quarts des valeurs de la série doivent être inférieures ou égales à Q₃. On calcule donc 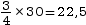. Q₃ correspond à la 23^e valeur de la série classée dans l’ordre croissant, soit Q₃= 41 m.

2. Les indicateurs de dispersion

a. L'étendue

L’étendue d’une série statistique est l’écart entre la plus grande et la plus petite valeur du caractère.

Exemple
Le tableau suivant donne la répartition des places dans un stade selon leur tarif.

Tarif en euros	15	20	30	40	100
Quantité en milliers	5	6	10	11	1

Ici la plus petite valeur est 15, et la plus grande 100. 100 – 15 = 85. L’étendue de cette série statistique est de 85 €.

b. L'écart interquartile

L’écart interquartile est égal à Q₃ – Q₁.
Cet indicateur permet de mesurer la dispersion des valeurs de la série statistique autour de sa moyenne. Plus il est grand, plus les valeurs sont dispersées.

Exemple
Reprenons l’exemple du paragraphe IC. L’écart interquartile vaut
41 – 39 = 2. Il est assez petit, ce qui signifie que les valeurs sont peu dispersées.

c. L'écart-type

Si on connait la moyenne d’une série statistique, on peut calculer sa variance par la formule :

L’écart-type noté

vaut

.
Il permet de mesurer la dispersion des valeurs de la série statistique autour de sa moyenne. Plus il est grand, plus les valeurs sont dispersées.

Exemple
Le tableau suivant donne le relevé des âges des élèves d’une classe :

Âge en années	14	15	16	17
Effectif	1	2	15	2

L’âge moyen des élèves de cette classe est de 15,6 ans.
On peut donc calculer la variance

= 0,44
D’où l’écart-type (arrondi au centième).

3. Comparer deux séries en choisissant les meilleurs indicateurs

Contrairement à la médiane et à l’écart interquartile, la moyenne et l’écart-type sont très sensibles aux valeurs extrêmes d’une série statistique.
Ainsi, lorsque l’on doit comparer deux séries, on commence souvent par observer l’effectif des valeurs extrêmes.

Si les valeurs extrêmes ont un effectif important, il est préférable de comparer les séries à l’aide de la médiane et de l’écart interquartile.
Sinon, on utilisera plutôt la moyenne et l’écart-type.

Exemple
En cours d’EPS, on a relevé les lancers de javelot de deux classes de 30 élèves.
Classe A :

Longueur en m	38	39	40	43	45
Effectif	5	6	4	7	8

Classe B :

Longueur en m	38	39	40	41	42	45
Effectif	8	4	4	4	2	8

Ici, les valeurs extrêmes des deux classes sont 38 et 45.
Dans la classe A, ces deux valeurs ont un effectif total de 13 (5 + 8), alors que l’effectif total de la série est de 30.
Dans la classe B, ces deux valeurs ont un effectif total de 16 (8 + 8), alors que l’effectif total de la série est de 30.
Les valeurs extrêmes ont un poids important dans ces deux séries, il est donc préférable de les comparer à l’aide de la médiane et de l’écart interquartile.

Pour la classe A :

Au moins un quart des valeurs de la série doivent être inférieures ou égales à Q₁. On calcule donc .
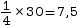Q₁ correspond à la 8^e valeur de la série classée dans l’ordre croissant, soit Q₁= 39 m.
Au moins trois-quarts des valeurs de la série doivent être inférieures ou égales à Q₃. On calcule donc .
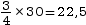Q₃ correspond à la 23^e valeur de la série classée dans l’ordre croissant, soit Q₃= 45 m.
On a donc un écart interquartile de 45 – 39 = 6 m.
La médiane vaut la moyenne de la 15^e et de la 16^e valeur, soit 41,5 m.

Pour la classe B :

Q₁ correspond à la 8^e valeur de la série classée dans l’ordre croissant. Soit Q₁= 38 m.
Q₃ correspond à la 23^e valeur de la série classée dans l’ordre croissant. Soit Q₃= 45 m.
Soit un écart interquartile de 45 – 38 = 7 m.
La médiane vaut la moyenne de la 15^e et de la 16^e valeur, soit 40 m.

Interprétation :
Dans la classe A, la moitié des élèves ont réalisé un lancer de plus de 41,5 m, alors que c’est seulement 40 m dans la classe B, donc un peu plus faible.
D’autre part, l’écart interquartile de la classe A est plus petit que celui de la classe B.
Au regard de ces deux indicateurs, la classe A semble être globalement meilleure (médiane supérieure à celle de la classe B) et plus homogène que la classe B (écart interquartile plus petit).

Évalue ce cours !

Note 4.1 / 5. Nombre de vote(s) : 21

Des quiz et exercices pour mieux assimiler sa leçon

La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

S’abonner

Des exercices variés pour ne pas s’ennuyer

Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !

Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

S’abonner

Des quiz pour une évaluation en direct

Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.

myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

S’abonner

Des vidéos et des podcasts pour apprendre différemment

Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.

Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

S’abonner

Des podcasts pour les révisions

La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.

Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

S’abonner

Des vidéos de cours pour comprendre en image

Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !

S’abonner

Profs en ligne

Découvrez le soutien scolaire en ligne avec myMaxicours

Plongez dans l'univers de myMaxicours et découvrez une approche innovante du soutien scolaire en ligne, conçue pour captiver et éduquer les élèves de CP à la terminale. Notre plateforme se distingue par une riche sélection de contenus interactifs et ludiques, élaborés pour stimuler la concentration et la motivation à travers des parcours d'apprentissage adaptés à chaque tranche d'âge. Chez myMaxicours, nous croyons en une éducation où chaque élève trouve sa place, progresse à son rythme et développe sa confiance en soi dans un environnement bienveillant.

Profitez d'un accès direct à nos Profs en ligne pour une assistance personnalisée, ou explorez nos exercices et corrigés pour renforcer vos connaissances. Notre assistance scolaire en ligne est conçue pour vous accompagner à chaque étape de votre parcours éducatif, tandis que nos vidéos et fiches de cours offrent des explications claires et concises sur une multitude de sujets. Avec myMaxicours, avancez sereinement sur le chemin de la réussite scolaire, armé des meilleurs outils et du soutien de professionnels dédiés à votre épanouissement académique.

EXERCE-TOI EN T'ABONNANT