Lycée > Terminale > Physique Chimie > Instruments à cordes, à vent et à percussion, ondes stationnaires

Instruments à cordes, à vent et à percussion, ondes stationnaires

Fiche de cours Quiz Profs en ligne Vidéos Télécharger le pdf

Fiche de cours Quiz Profs en ligne Vidéos Télécharger
le pdf

Objectifs

Pour jouer de la musique, les musiciens utilisent des instruments dont la diversité de forme et de fonctionnement est à l'origine de la richesse.
• Mais qu’est-ce qu’un instrument de musique ?
• Comment peut-on les classer ?
• Quels sont les phénomènes physiques mis en jeu par les instruments ?

1. Description des instruments de musique

Un instrument de musique est un objet qui est capable d’émettre un son musical, audible et agréable à écouter.
L’instrument est notamment caractérisé par son timbre (poids des diverses harmonique du son, voir la fiche sur les caractéristiques des sons musicaux) et sa tessiture, c'est-à-dire l’ensemble des notes pouvant être jouées avec lui.
Tous les instruments de musique sont constitués d’un vibrateur et d’un résonateur.

a. Le vibrateur

Un instrument de musique est constitué d’un corps mécanique qui entre en vibration : le vibrateur.
Cela peut être :
– une corde pour le violon ;
– une anche pour la clarinette ;
– une membrane tendue pour le tambour ;
– une pièce métallique ou en bois pour le xylophone.

Lorsqu’il est excité, le vibrateur se met en vibration et transmet ces vibrations à l’air.
Le vibrateur n’est pas capable de faire vibrer suffisamment les tranches d’air pour que le son émis soit audible, il faut donc le coupler à un résonateur.

b. Le résonateur

Tous les instruments de musique ont un résonateur qui permet au son d’être amplifié et transmis aux couches d’air jusqu’aux oreilles du musicien et de ses auditeurs.
Le résonateur, aussi appelé caisse de résonance, est soit le corps de l’instrument comme pour le saxophone, soit une caisse comme pour la guitare. Le résonateur peut amplifier sélectivement certaines fréquences.
Le timbre des notes émises, qui est en quelque sorte la « signature » de l’instrument, est ainsi dû au résonateur.

2. Les familles d'instruments de musique

Les instruments sont généralement classés en trois familles : les instruments à cordes, les instruments à vent et les instruments à percussion. Nous verrons dans une autre fiche que l’on peut aussi leur rajouter les instruments électroniques.

a. Les instruments à cordes

Le vibrateur des instruments à cordes est une corde tendue entre deux points fixes.

La corde peut être :

– frottée avec un archet, comme pour le violon ;

– frappée avec un marteau dans le cas du piano ;
– pincée avec le doigt pour la harpe et de la guitare.

Le nombre de cordes, leur grosseur et leur longueur varient d’un instrument à l’autre.
Certains instruments, comme le piano, ont de nombreuses cordes, chacune correspondant à une note. D'autres, comme le violon, ont un petit nombre de cordes, dont il faut faire varier la longueur avec le doigt pour balayer toutes les notes de la tessiture de l’instrument.

Exemple d'instrument :
Le piano est un instrument à cordes frappées. Le musicien joue sur un clavier, lequel est relié à un mécanisme qui met en mouvement des petits marteaux qui frappent les cordes. Les vibrations de ces dernières sont transmises, par l’intermédiaire d’une pièce nommée chevalet à une plaque de bois, la table d’harmonie. Chacune des cordes est tendue et joue le rôle du vibrateur. La table d’harmonie est quand à elle la pièce principale du résonateur. La vibration d’une corde est arrêtée par l’étouffoir (un morceau de feutre) qui se pose rapidement sur la corde dès que la touche n’est plus enfoncée.

b. Les instruments à vent

Avec les instruments à vent, le musicien souffle pour mettre en vibration l’air contenu dans son instrument. Les instruments à vent en bois, comme la flûte ou le hautbois, ont une anche, simple ou double, placée à l’embouchure. Celle-ci vibre et met alors en résonance l’air présent au sein de l’instrument. Les instruments à vent de la famille des cuivres, comme la trompette, sont un peu différents : ce sont les lèvres du musicien, qui, par leurs vibrations et leurs mouvements, mettent l’air en vibration.

Exemple d'instrument :

La clarinette est un instrument à vent en bois. Elle se compose d’un bec (l’embouchure), dans lequel se trouve une anche simple, avec un corps et un pavillon (bas du corps).
Le corps de la clarinette, percé de 24 trous, possède 17 clés qui, combinées par les doigts du clarinettiste, permettent d’obtenir des sons étendus sur trois octaves.

c. Les instruments à percussion

Les instruments à percussion se répartissent en deux catégories : les membranophones et les idiophones.
Les membranophones, comme le tambour, sont construits autour d’une membrane qui vibre au-dessus d’une caisse de résonance.
Les idiophones sont des instruments dont le corps est lui-même le résonateur ; c'est la cas du triangle.

Le son émis par certains instruments à percussion peut être de hauteur constante : l’instrument n’émet qu’une seule note, toujours identique.

3. Modélisation physique du vibrateur : les ondes stationnaires

a. Les ondes stationnaires au sein d’une corde, avec un point fixe

Une onde progressive transversale peut évoluer au sein d’une corde tendue (voir fiche sur les ondes progressives périodiques). La célérité v (en m/s) de cette onde est donnée par

où F est la force (en N) mettant la corde sous tension, μ est la masse linéique (en kg/m) de la corde, c'est-à-dire la masse d’un mètre de corde. v est reliée à la fréquence f (en Hz) de l’onde, à sa période T (en s) et à sa longueur d’onde λ (en m), par la double égalité :

On provoque une perturbation au niveau d’une extrémité (point A) d’une corde tendue. Cette perturbation va alors se propager. Si l’on fixe l’autre extrémité (point B) de la corde, la perturbation « rebondira » sur ce point B, et repartira en sens inverse.

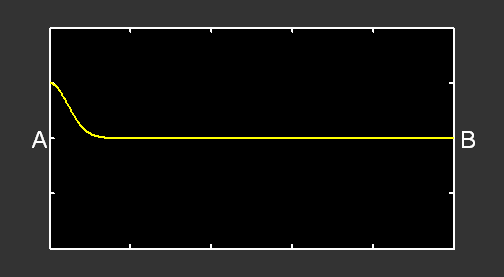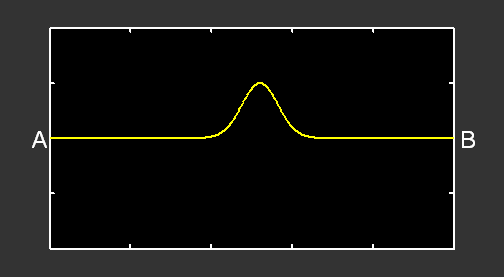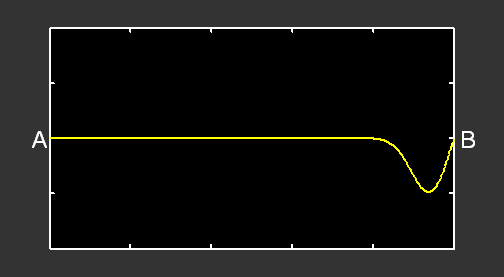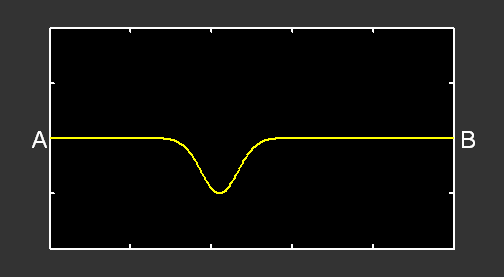
Si l’on remplace la perturbation par une oscillation sinusoïdale, nous obtenons :

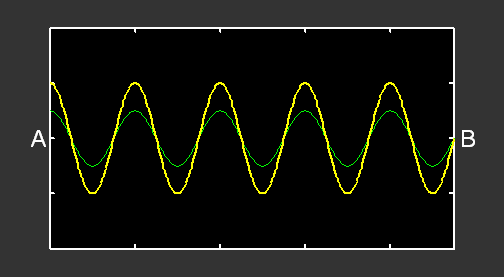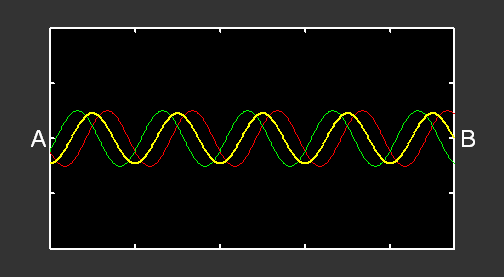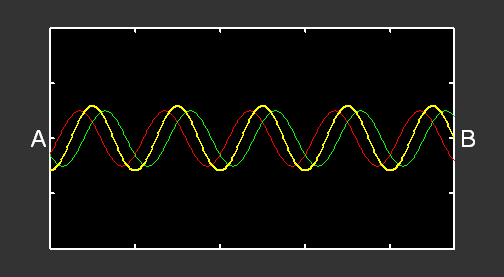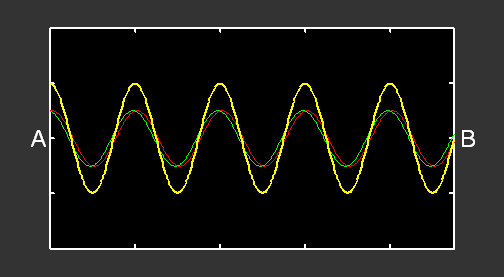
L’oscillation produite en A induit la formation d’une onde progressive sinusoïdale allant de gauche à droite (courbe verte). Quand cette onde arrive en B, elle est réfléchie et il se forme alors une autre onde progressive, allant de droite à gauche (courbe rouge). Le mouvement de la corde correspond à la superposition de ces deux ondes progressives (courbe jaune).

Ce mouvement n’est pas une onde progressive, mais une onde stationnaire. En effet, seule l’amplitude de cette onde varie au cours du temps : elle ne se propage pas, d’où son nom. Certains points de la corde n’oscillent jamais : ce sont des nœuds de vibration. Au contraire, des points oscillent avec une amplitude maximale par rapport aux autres : ce sont des ventres de vibration.

b. Propriétés des ondes stationnaires avec deux points fixes

Le même phénomène est observé si l’on fixe les deux extrémités de la corde, et que l’on met la corde en vibration, en la pinçant ou en la frappant comme avec une corde d’un instrument de musique. La mise en vibration provoque la formation d’ondes progressives, qui se propagent dans les deux sens (gauche/droite et droite/gauche). La superposition de ces ondes donne une onde stationnaire. Dans la pratique, cette vibration étant rapide, la corde apparaît sous la forme d’un ou plusieurs fuseaux. Le milieu d’un fuseau est un ventre de vibration. Les extrémités de la corde et/ou le point séparant deux fuseaux consécutifs sont des nœuds.

En ayant deux points fixes, la différence majeure avec ce que l’on a vu plus haut est que seules certaines fréquences de vibrations sont permises : elles sont quantifiées. Pour une corde de longueur L (en m), on a 2L = n × λ, où n est un nombre entier strictement positif, correspondant au nombre de fuseaux observés, et λ (en m) est la longueur d’onde de l’onde stationnaire. On peut relier λ à la fréquence f via la relation v =

= λ × f avec

, ces formules restant utilisables avec les ondes stationnaires.

Lorsque n = 1, un seul fuseau est visible ; la corde vibre selon son mode fondamental. La longueur d’onde λ vaut alors le double de la longueur L de la corde. La fréquence du mode fondamental,

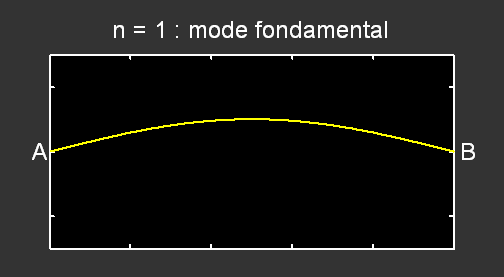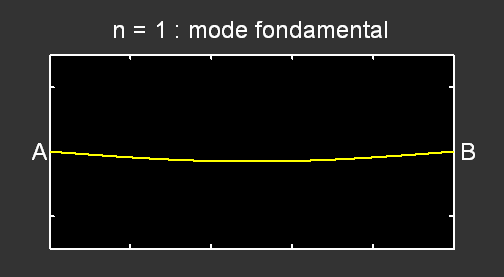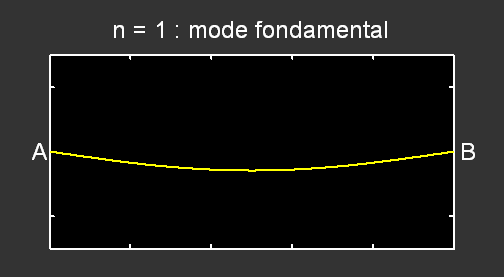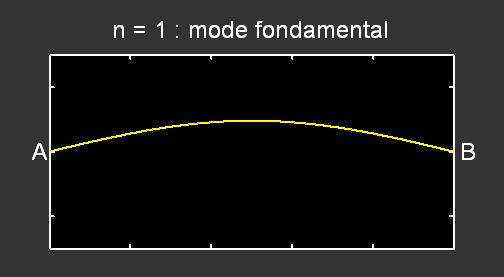
, est la fréquence non nulle la plus faible permise : toutes les autres fréquences permises sont multiples de celle-ci.

Pour le mode n = 2 , la fréquence correspondante vaut f₂ = 2 × f₁ et pour n = 3, f₃ = 3 × f₁ :

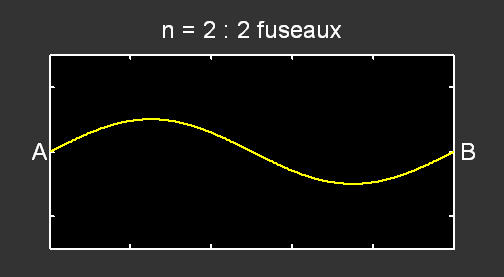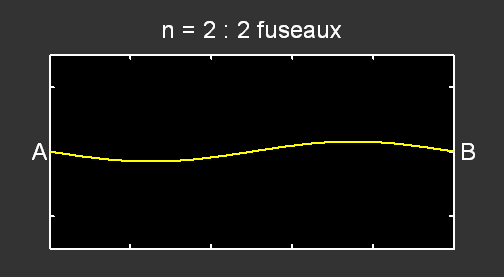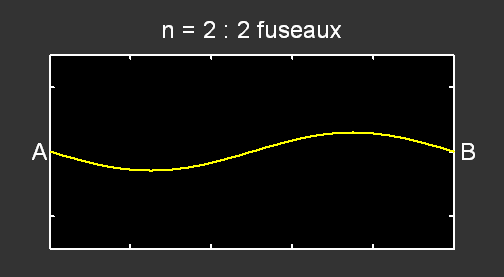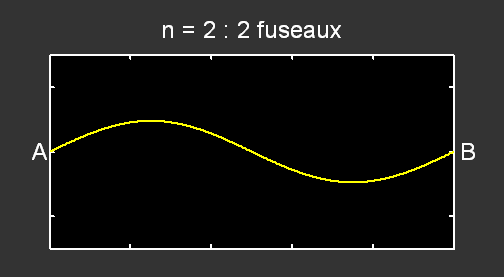
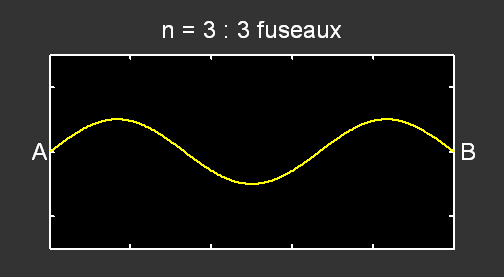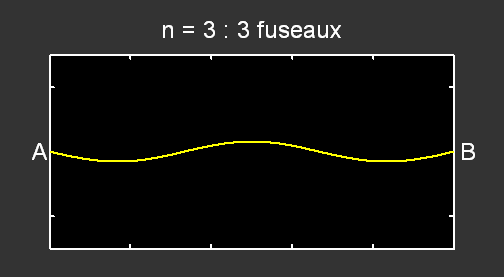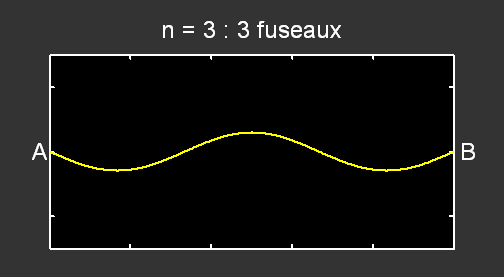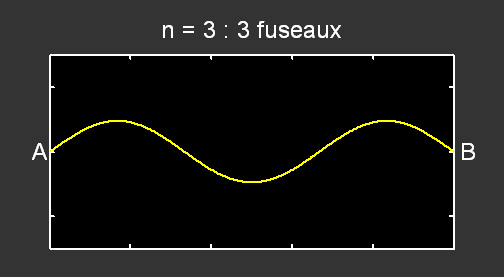
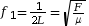c. Applications des ondes stationnaires en musique

→ Dans les instruments à corde, les ondes stationnaires apparaissent lorsque l’on fait vibrer une corde du vibrateur de cet instrument. Comme la corde est fixée à ses deux extrémités, elle ne peut vibrer que selon certaines fréquences. Le mode fondamental est le plus étudié. En agissant sur certains paramètres, on peut modifier la valeur de la fréquence fondamentale

.

Par exemple, en raccourcissant la longueur mise en vibration de la corde (on diminue L), on augmente la fréquence, et on émet alors un son plus aigu. On peut donc modifier la hauteur du son joué en agissant sur L. C’est ce qu’il se passe avec une guitare, en modifiant la position des doigts de la main gauche (qui appuient sur les cordes), au niveau du manche de l’instrument.

→ Pour des instruments à vent (exemple : orgue), le comportement de la colonne air présente au sein de l’instrument est décrit avec les ondes stationnaires. La différence avec la corde est l’on raisonne par rapport à la pression et/ou la vitesse de l’air contenu dans la colonne. Une propriété est qu’un nœud de vitesse correspond à un ventre de pression, et inversement.

→ Les vibrations de la membrane d’un tambour sont aussi décrites par des ondes stationnaires. Mais, les ondes au sein de la corde sont monodimensionnelles, alors que celles de la membrane sont bidimensionnelles.

L'essentiel

Un instrument de musique est constitué d’un vibrateur et d’un résonateur. Il existe plusieurs familles d’instruments : les instruments à cordes, à vent et les percussions.

On peut modéliser la vibration d’une corde d’un vibrateur à l’aide des ondes stationnaires. Contrairement à une onde progressive, une onde stationnaire ne se propage pas. Si la corde est fixée à ses deux extrémités, les fréquences/longueurs d’onde d’une onde stationnaire sont quantifiées, et obtenues par la relation 2L = n × λ.

Vous avez déjà mis une note à ce cours.

Découvrez les autres cours offerts par Maxicours !

Découvrez Maxicours

Comment as-tu trouvé ce cours ?

Évalue ce cours !