Exploitation d'un spectre de fréquence
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Comment ces caractéristiques peuvent-elles être déterminées à partir d'un spectre de fréquence ?
On observe ainsi qu’un son complexe est composé de différents signaux sinusoïdaux de différentes fréquences.
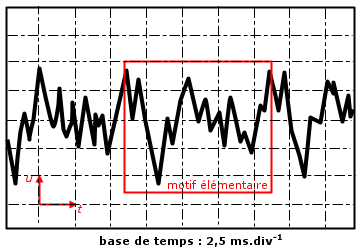
Doc. 1. Courbe u(t) = f(t) obtenue en frottant une corde d’un violon.
À partir des données de cette courbe
et à l’aide d’un logiciel
d’analyse de spectre qui permet de calculer les
différentes fréquences des signaux
sinusoïdaux qui constituent le son complexe, on
obtient le spectre de fréquence correspondant
:
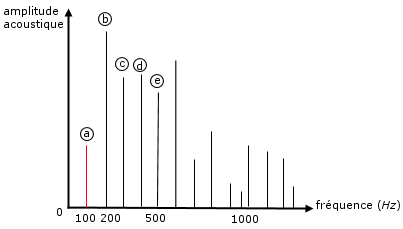
Doc. 2. Spectre de fréquence de la courbe du document 1.
Le spectre de fréquence d’un son
pur (ou son simple) n’est composé
que d’un seul pic qui correspond à la
fréquence du mode de vibration
fondamentale (ou simplement fréquence
fondamentale).
Le spectre de fréquence d’un son
complexe est composé de plusieurs
pics correspondants à la
fréquence du mode fondamental et celles de ses
harmoniques.
|
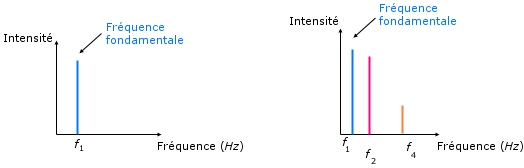
a. Son pur : |
b. Son complexe : |
|
|
| Doc. 3. Spectres de fréquences : a. son pur ; b. son complexe. | |
Chaque mode de vibration est représenté par un segment de droite dont l'abscisse donne la fréquence du mode et dont la hauteur du pic est proportionnelle à l'intensité (ou amplitude) du son.
On associe à la hauteur d’un son
la fréquence de son mode de
vibration fondamentale.
Sur un spectre de fréquence, la hauteur
d’un son est donc déterminée par la
fréquence, f1, du premier
pic.
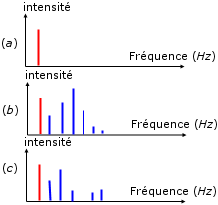
Doc. 4. Spectres de la note La émise par trois instruments.
Ces spectres ont même hauteur
(même fréquence fondamentale) : ils
correspondent bien à une même note de
musique.
Ils ont des timbres différents
puisqu’ils sont composés
d’harmoniques de même fréquence mais
d’intensités différentes (le
cinquième harmonique du spectre (c) a une
intensité nulle).
Plus l’amplitude des vibrations sonores émises est grande, plus l’intensité du son émis est forte et plus les pics du spectre de fréquence ont une hauteur élevée (attention aux échelles de l’axe verticale des différents spectres obtenus).
On peut aussi utiliser les spectres de fréquence pour comprendre le principe de construction de la gamme tempérée, et ainsi pouvoir jouer des œuvres complexes.
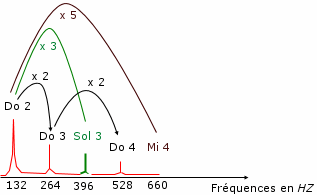
Doc. 5. Spectre du Do 2 (octave 2)
joué par un instrument.
On observe bien que pour une même
note (le do ici), pour passer d’une octave
à une autre, il suffit de multiplier la
fréquence par 2 .
Le spectre en fréquence du Do 2 permet
également de comprendre que, pour une oreille
"européenne", l'accord majeur Do-Mi-Sol soit
harmonieux, puisque ces trois notes ont des harmoniques
communes.
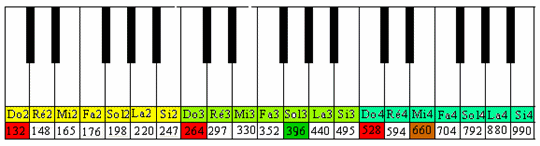
Doc. 6. Fréquences des différentes notes d'un piano.
La plupart des téléphones actuels sont
dits à numérotation à
fréquence vocale. Chaque numéro est
caractérisé par sa position sur le
clavier (ligne, colonne).
Lorsque l'on appuie sur une touche, le signal
émis résulte de la superposition de deux
signaux sinusoïdaux de fréquences
distinctes, l'une caractéristique de la ligne et
l'autre de la colonne (doc. 7).
| 1 209 Hz | 1 336 Hz | 1 477 Hz | |
| 697 Hz | 1 | 2 | 3 |
| 770 Hz | 4 | 5 | 6 |
| 852 Hz | 7 | 8 | 9 |
| 941 Hz | * | 0 | # |
Doc. 7. Fréquences des
touches d'un téléphone.
De ce fait, le' son émis lorsqu'on appuie sur le 5 du clavier correspond à la superposition d'une sinusoïde de fréquence 770 Hz et d'une autre de fréquence 1 336 Hz.
Le spectre de fréquence du son correspondant présente deux pics (doc. 8) :
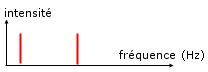
Doc. 8. Spectre de
fréquence de la touche 5 du
téléphone.
– sa hauteur, caractérisée par sa fréquence du mode de vibration fondamental ;
– son timbre (il dépend de la composition des harmoniques) permet de distinguer deux notes de même hauteur jouée par deux instruments différents ;
– son intensité, liée à la hauteur des pics du spectre.
• À partir des spectres de fréquence, on peut analyser les sons et en particulier les notes et ces harmoniques qui le composent. Ce son pourra alors être reproduit à l’identique par des instruments ou par un synthétiseur de son. Il pourra être également modifié ou utilisé dans d’autres applications.
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Physique Chimie
Applications à des titrages mettant en jeu des réactions acido-basiques
Physique Chimie
La démarche scientifique, relation science-société
Physique Chimie
Métiers de l'activité scientifique
Physique Chimie
Instruments électroniques
Physique Chimie
Voix : acoustique physiologique
Physique Chimie
Réverbération acoustique : auditorium, salle sourde
Physique Chimie
Isolation phonique
Physique Chimie
Application des ondes acoustiques : le sonar et l'échographie
Physique Chimie
Reconnaissance vocale
Physique Chimie
Production de dihydrogène
Fermer
Accédez gratuitement à
