Lycée > Terminale > Physique Chimie > Caractéristiques des sons musicaux

Caractéristiques des sons musicaux

Fiche de cours Quiz Profs en ligne Vidéos Télécharger le pdf

Fiche de cours Quiz Profs en ligne Vidéos Télécharger
le pdf

Objectifs :

Cette fiche est une fiche de synthèse concernant les sons musicaux. En effet, elle reprend certaines notions liées au programme obligatoire, comme l’analyse fréquentielle, l’intensité acoustique, et certaines notions de spécialité, comme l’enveloppe d’un son.

La plupart des signaux sonores utilisés en musique sont complexes. Pour les décrire, les musiciens leur associent des caractéristiques telles que la hauteur, le timbre, l’enveloppe et l’intensité. Ces caractéristiques sont associées à des grandeurs physiques. Dans cette fiche, nous proposons d’étudier les liens entre ces termes musicaux et ces grandeurs physiques, et de voir leur influence sur la perception auditive.

1. Types de son

a. Son pur

Un son pur, ou son simple, correspond à une onde sinusoïdale dont la fréquence ne varie pas au cours du temps. Dans la pratique, on pourra considérer des sons purs dont l’amplitude est également constante pendant un certain laps de temps. Le son émis par le diapason est un exemple de son pur.

b. Son complexe et son musical

La plupart des sons que nous percevons dans notre environnement ne sont pas purs mais complexes. Ils sont composés de plusieurs sons purs de fréquences et d’amplitudes différentes. Un son musical est un cas particulier de son complexe, produit par un instrument de musique. Parmi les propriétés d’un son musical, nous retiendrons pour l’instant qu’un son musical est périodique (de période constante au cours du temps), mais n’est pas forcément sinusoïdal.

c. Analyse fréquentielle d'un son périodique

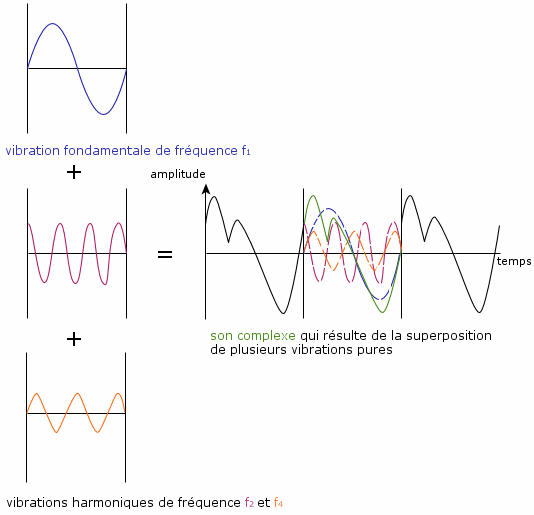Comme vu dans la fiche « Analyse spectrale », tout signal périodique peut se décomposer en une somme de sinusoïdes, d’après le théorème de Fourier. Ainsi, un son musical est la résultante de la superposition de plusieurs vibrations : la vibration fondamentale de fréquence f₁ , sur laquelle s’ajoutent des vibrations harmoniques dont les fréquences sont des multiples de la première.

Vibrations résultant de la superposition d'harmoniques

Les graphes ci-dessus décrivent les vibrations pour des harmoniques de fréquence f₁, f₂ = 2f₁ et f₄ = 4f₁ . Il s'agit d'un son musical complexe. Les analyseurs d'harmoniques permettent de décomposer ce type de sons. Le résultat graphique d'une telle analyse est appelé spectre des fréquences ou spectre de Fourier.

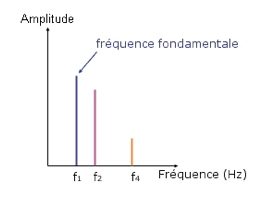
Spectre des fréquences du son à harmonies multiples

Chaque harmonique est représentée par un segment de droite (pic) dont l'abscisse donne la fréquence de la vibration associée.
La longueur de chaque segment est proportionnelle à l'amplitude de la vibration. Le spectre de Fourier d'un son pur n'est constitué que d'un seul pic associé à la fréquence du son.

2. Hauteur d'un son musicial

a. Définition

La hauteur d’un son correspond à la fréquence de son mode de vibration fondamental, exprimée en hertz (symbole : Hz). La hauteur d’un son est associée au nom de la note jouée (do, ré, mi, ... d’une certaine octave). Le terme de hauteur vient du fait que les notes sont écrites sur une portée musicale de telle manière que la position verticale de la note sur la portée correspond à son nom. La hauteur d’un son est la caractéristique qui permet de dire si un son est aigu ou grave.

Lorsque les sons musicaux se succèdent ou se superposent, l’oreille est sensible au rapport de leur hauteur, ce qui fait que certains enchaînements de sons musicaux sont agréables à l’oreille, ou non.

b. Les différentes notes de musique

Comme nous venons de le voir, chaque note est caractérisée par une fréquence fondamentale déterminée. Lorsque deux notes sont séparées d’une octave, le rapport de leur fréquence est égal à deux. Dans la pratique, ces deux notes ont le même nom, comme par exemple le la de l’octave 3 et le la de l’octave 4, nommée couramment la3 et la4 pour éviter toute ambigüité entre elles.

On appelle gamme l’ensemble des notes composant une octave donnée. Dans la gamme tempérée, c'est-à-dire celle utilisée dans la musique occidentale, l’octave est divisée en 12 demi-tons, ce qui correspond à 12 notes, en comptant les notes diésées (#). Le rapport des fréquences de 2 notes consécutives, donc séparées par un demi-ton, est de 2^1/12 . En conséquence, les fréquences des notes d’une gamme suivent une progression géométrique de raison 2^1/12 (cf. suites géométriques).

Octave	do	do#	ré	ré#	mi	fa	fa#	sol	sol#	la	la#	si
3	261,63	277,18	293,66	311,13	329,63	349,23	369,99	392,00	415,30	440,00	466,16	493,88
4	523,25	554,37	587,33	622,25	659,26	698,46	739,99	789,99	830,61	880,00	932,33	989,77

Fréquences fondamentales des notes des octaves 3 et 4

3. Notion de timbre

Deux sons musicaux correspondant à une même note (même fréquence fondamentale), mais émis par deux instruments différents ne sont pas perçus de la même façon par l’oreille. On dit alors que ces deux sons n’ont pas le même timbre. Autrement dit, le timbre d’un son dépend de l’instrument qui émet ce son. Les oscillogrammes (courbes bleues ciel) de deux sons musicaux de même hauteur nous permettent de vérifier que ces deux sons ont même période, donc même fréquence fondamentale. Par contre, les allures de ces deux sons en fonction du temps son très différentes. Les spectres de Fourier des deux sons font apparaître des harmoniques de mêmes fréquences, mais d’amplitudes différentes d’un son à l’autre.

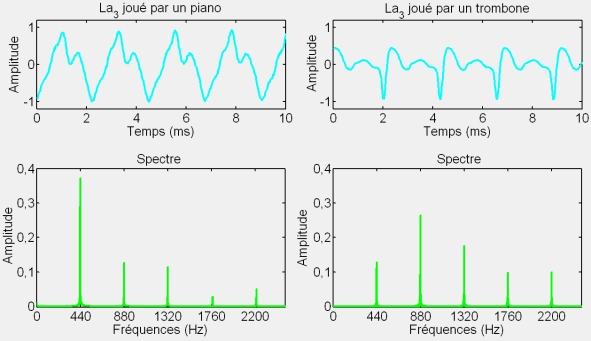
Physiquement, la notion de timbre s’explique ainsi par le poids des harmoniques composant les sons musicaux étudiés. Autrement dit, le timbre d’un son musical peut être caractérisé par la forme de son spectre en fréquences : nombre et amplitudes relatives des harmoniques.

4. Enveloppe d'un son musical

Une note a un début et une fin. L’oscillogramme d’une note, indiquant son évolution au cours du temps, est complexe. Il se compose de quatre phases : attaque, déclin, maintien (corps de la note) et extinction. La courbe décrivant l’évolution de l’amplitude du son au cours du temps est l’enveloppe du son musical. L’enveloppe dépend de l’instrument utilisé et de la manière d’en jouer.
Exemple : façon d’appuyer sur les touches d’un piano, durée pendant laquelle on souffle dans un instrument à vent, etc.

Remarque : le poids de chaque harmonique peut varier entre l’attaque et l’extinction. Ainsi, il n’y a pas que l’amplitude du son qui varie au cours du temps : le spectre du son est susceptible d’évoluer également.

5. Intensité acoustique et niveau sonore

a. Puissance acoustique d'une source sonore

On peut caractériser une source sonore par sa puissance acoustique W, qui est l’énergie par unité de temps emportée par l’onde sonore émise. Une puissance acoustique s’exprime, comme toute puissance, en Watts. Lorsque l’on se trouve à une distance fixe de la source, si l’on augmente la puissance acoustique de cette dernière, alors on percevra un son plus fort.

b. Intensité acoustique d'un son reçu

Considérons une source sonore, émettant à une certaine puissance acoustique W constante. Si l’on s’éloigne de la source, on perçoit un son moins fort.

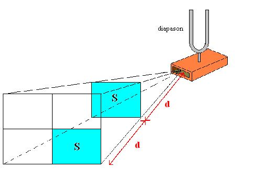
Pour comprendre ce phénomène, nous considérons que la source est ponctuelle et que le son se propage dans l’air sans rencontrer d’obstacle. Le son se propage alors dans un espace tridimensionnel. Ses fronts d’onde sont des sphères centrées sur la source émettrice, dont les rayons augmentent avec le temps, au fur et à mesure que le son se propage. À un instant donné, la puissance acoustique W émise se répartit sur la surface d’une sphère de rayon R. S’il n’y a pas absorption par le milieu de propagation, W est conservée.

La sensation qu’un son perçu soit fort ou pas est liée à l’intensité acoustique I du son, exprimée en W/m² , et liée à W par la relation :

I est ainsi une puissance surfacique (puissance par unité de surface). En conséquence, plus on se place loin de la source, c'est-à-dire plus le rayon R de la sphère est grand, plus l’intensité acoustique I du son perçu sera faible, et donc plus on percevra ce son comme faible. D’ailleurs, la formule nous permet de voir que si l’on double R, alors on divise I par quatre. Ainsi, un récepteur sonore (ex : tympan d’une oreille), de surface s reçoit une intensité acoustique quatre fois plus faible quand sa distance à la source émettrice double.

En résumé, l’intensité acoustique I est définie comme la puissance sonore reçue par unité de surface (par ex. du récepteur). Elle se mesure en Watts par mètre carré (W/m²). Pour un même récepteur, elle est fonction de la distance entre l’émetteur et le récepteur.

Remarque (non exigible) : l’intensité acoustique est proportionnelle au carré de l’amplitude de l’onde sonore.

c. Niveau sonore

Le niveau sonore L sert à exprimer combien de fois une intensité sonore I est plus grande qu’une autre prise comme référence, dans une échelle logarithmique (voir fiche sur le décibel). Le niveau sonore L est définit comme :

L s’exprime en décibels acoustiques (symbole : dBA) et est mesurée avec un sonomètre. I₀ est une intensité acoustique prise comme référence, qui correspond au seuil d’audibilité théorique de l’oreille humaine aux environs de 1000-2000 Hz. En effet, l’oreille humaine perçoit des sons dont les fréquences sont comprises entre 20 Hz et 20 kHz, mais la sensibilité de l’oreille varie avec la fréquence. Elle est ainsi maximale autour de un ou deux kHz. On a alors I₀ = 10^–12 , correspondant à un niveau sonore L = 0 dB . Pour information, le seuil de la sensation douloureuse est de l’ordre de 120 dB.

L'essentiel

Un son musical émis est défini par :

• sa hauteur, caractérisée par sa fréquence fondamentale. Le nom d’une note est lié à sa hauteur, donc à sa fréquence fondamentale. Dans la gamme tempérée, le rapport des fréquences de deux notes consécutives au sein d’une octave est égal à 2^1/12.

• son timbre, qui dépend de la composition des harmoniques, permet de distinguer deux notes de même hauteur jouées par deux instruments différents.

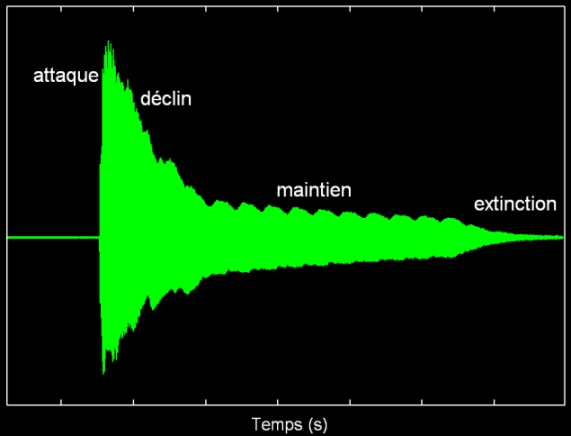
• son enveloppe, c'est-à-dire la manière dont évolue son amplitude au cours du temps.

• son intensité acoustique I, qui permet de différentier un son perçu comme fort d’un son faible. I est la puissance sonore reçue par unité de surface. Elle s’exprime en W / m². On associe l’intensité acoustique au niveau sonore L défini par