Exploiter une série de mesures
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Connaitre le vocabulaire lié à une mesure.
- Exploiter l’histogramme d’une série de mesures.
- Estimer la valeur vraie d’une série de mesures grâce à la moyenne.
- Estimer la dispersion d’une série de mesures grâce à l’écart-type.
- Toute mesure comporte des erreurs.
- Les résultats de mesures peuvent être utilisés pour en estimer la valeur vraie.
- On utilise un histogramme pour visualiser la dispersion des mesures.
- On utilise la valeur moyenne pour estimer la valeur vraie et l’écart-type pour mesurer la dispersion des mesures autour de cette moyenne.
Statistiques : regroupement en classes, histogramme, moyenne, écart-type
En physique-chimie, on réalise souvent des séries de mesures durant les travaux pratiques.
Le processus expérimental qu’on met en œuvre à cet effet s’appelle le mesurage.
- On mesure l’intensité d’un courant électrique à l’aide d’un ampèremètre.
- Le mesurande est la valeur de l’intensité.
- Le mesurage est effectué avec un ampèremètre.
Une mesure n’est jamais exacte car les appareils
et protocoles comportent des imperfections.
Le but d’une mesure est d’estimer la valeur
« vraie » d’une grandeur physique.
Voici une série de 20 mesures d’une intensité électrique i en milliampère.
| 151,9 | 152,4 | 145,6 | 149,7 | 150,8 | 153,1 | 147,8 | 147,5 | 150,3 | 149,1 |
| 146,3 | 148,6 | 152,5 | 151,2 | 150,3 | 149,4 | 150,7 | 150,1 | 152,8 | 149,4 |
On cherche à construire l'histogramme de cette série de mesures : on regroupe pour cela des valeurs en classes (intervalles de valeurs).
L'histogramme va représenter l'effectif en fonction des valeurs d'intensité.
Il y a par exemple 3 mesures dans la classe
[152 ; 153[.
En regroupant toutes les valeurs, on obtient
l'histogramme suivant.
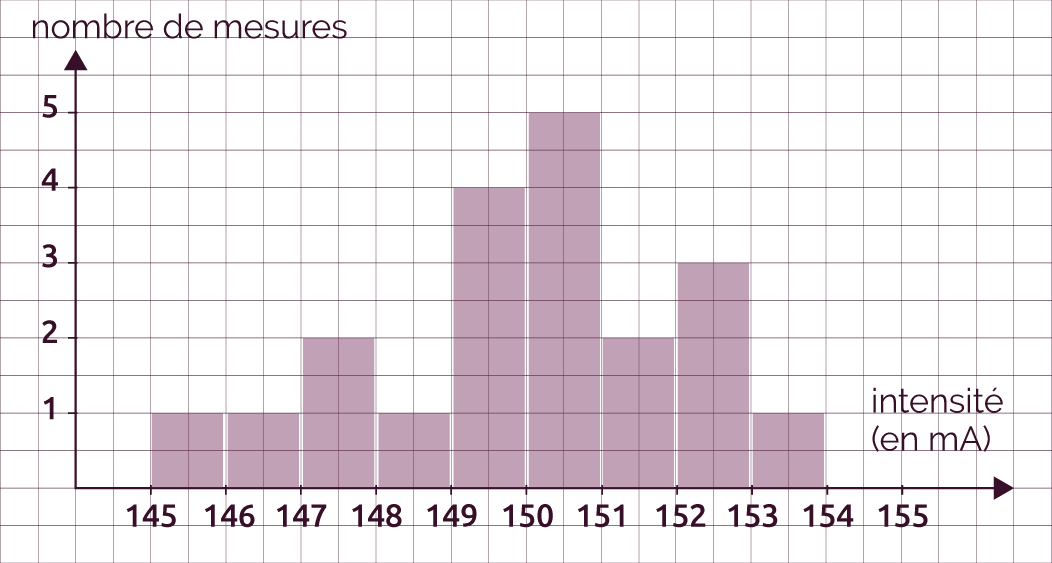
Histogramme obtenu pour 20 mesures
La représentation graphique en histogramme donne un bon aperçu de la dispersion des mesures.
Cette courbe donne des indications sur des indicateurs statistiques, que nous allons voir par la suite.
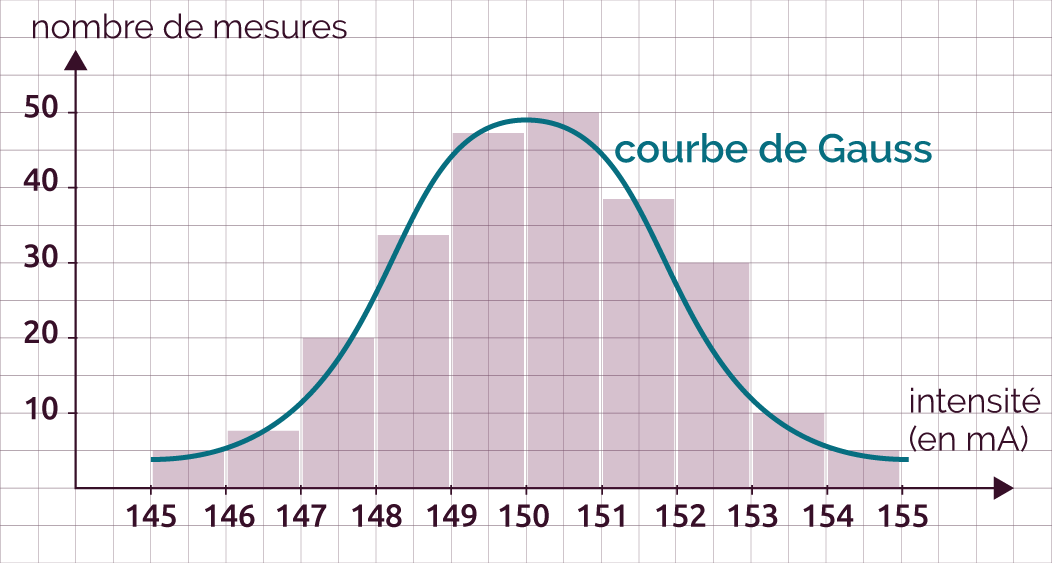
Histogramme obtenu pour 250 mesures
Si on effectue N mesures
(x1 ; x2 ; … ; xN),
la meilleur estimation de la valeur vraie est la
valeur moyenne 
des N mesures, telle
que :
On reprend ci-dessous la série de 20 mesures d’intensité étudiée précédemment.
| 151,9 | 152,4 | 145,6 | 149,7 | 150,8 | 153,1 | 147,8 | 147,5 | 150,3 | 149,1 |
| 146,3 | 148,6 | 152,5 | 151,2 | 150,3 | 149,4 | 150,7 | 150,1 | 152,8 | 149,4 |
La calculatrice (en mode statistique) donne
= 150,0 mA
(le calcul consiste à sommer toutes les
valeurs de ce tableau et à diviser par
le nombre de valeurs, ici 20).
Une estimation de la valeur vraie de
l’intensité mesurée est donc
150,0 mA.
La valeur vraie (ou valeur moyenne) peut également être estimée graphiquement, comme étant l’abscisse qui coupe l’axe de symétrie de la courbe de Gauss.
Sur l’histogramme ci-dessous, on peut estimer graphiquement que la valeur vraie de l’intensité est 150 mA.
Les valeurs de l'intensité mesurées sont dispersées de part et d'autres de cette valeur vraie.
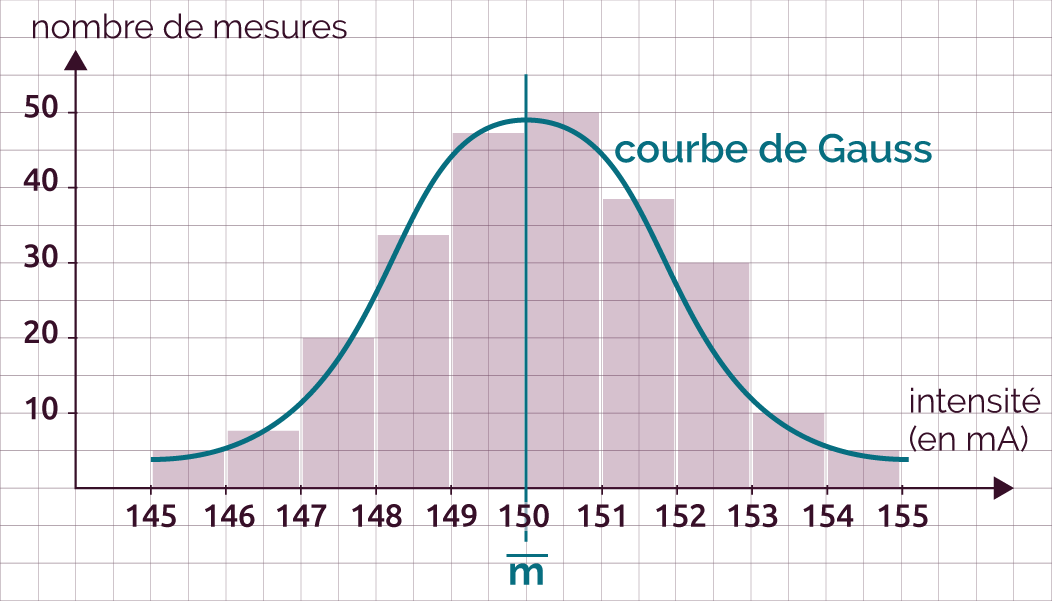
Estimation graphique de la valeur moyenne
.
L'écart-type se calcule avec un
tableur, une calculatrice ou à l’aide de
la formule suivante.
On reprend la série de mesures sur l’intensité précédente.
À l’aide d’un tableur, on trouve un écart-type
= 2,14 mA.
- On n’utilise pas le même
écart-type en physique (
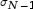) qu’en
mathématiques (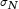
).
- En physique, on utilise l’écart-type
expérimental. Il se lit
« x
n–1 » avec
Casio et « Sx »
avec Texas Instrument.
- En mathématiques,
l’écart-type se lit
« x
n » sur une
Casio et « 
x » sur une
Texas Instrument.
L’écart-type mesure la dispersion (l’étalement) des valeurs autour de la valeur moyenne.
est petit,
plus les valeurs sont resserrées autour de la
moyenne et donc de la valeur vraie.
On étudie l’histogramme de deux séries de mesures
(la série n° 1 correspond aux valeurs étudiées précédemment).
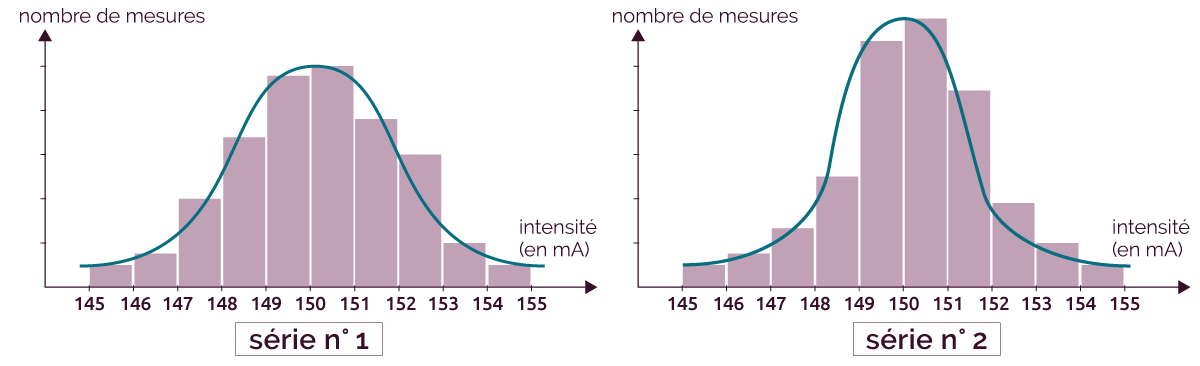
Histogramme de deux séries de mesures
On a donc
, ce qui signifie que les
mesures de la série n° 2 ont plus de chance
d’être proches de la valeur vraie.
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
Fermer
Accédez gratuitement à
