Fiche de cours

Les modèles démographiques

Lycée > Terminale > Sciences > Les modèles démographiques

Fiche de cours
Quiz et exercices
Vidéos et podcasts

Objectifs :

Exprimer u_n en fonction de u₀ et n, pour des suites arithmétique et géométrique.
Produire et interpréter des graphiques statistiques traduisant l’évolution d’effectif d’une population ou de ressources, sous forme de nuages de points.
À l’aide d’une calculatrice ou d’un tableur, ajuster un nuage de points par une droite et utiliser ce modèle linéaire pour effectuer des prévisions.
Calculer le taux de variation d’une population entre deux dates.
Calculer l’effectif final d’une population à partir de son effectif initial, de son taux de natalité et de son taux de mortalité.
Selon le modèle de Malthus, prédire l’effectif d’une population au bout de n années.
À l’aide d’un tableur, d’une calculatrice ou d’une représentation graphique, calculer le temps de doublement d’une population sous l’hypothèse de croissance exponentielle.
Proposer un modèle de croissance de ressources alimentaires et la comparer à une croissance exponentielle.
Comparer les valeurs fournies par un modèle à des données réelles afin de tester la validité du modèle.

Points clés :

Une grandeur discrète u varie de manière linéaire en fonction d’un palier entier n, si sa variation absolue [u_n+1 – u_n] est constante.
Pour certaines populations, la variation absolue [u_n+1 – u_n] est presque constante d’un palier à l’autre. Les points de la suite représentant l’évolution de la population sont alors presque alignés. Dans ce cas, on peut ajuster le nuage de points par une droite. Le modèle est alors qualifié de linéaire.
Une grandeur discrète u varie de manière exponentielle en fonction d’un palier entier n, si sa variation absolue [u_n+1 – u_n] est proportionnelle à u_n.
Pour certaines populations, la variation relative 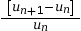est presque constante d’un palier à l’autre. L’allure du nuage de points représentant l’évolution de la population se rapproche alors d’une courbe exponentielle. Dans ce cas, on peut ajuster le nuage de points par une courbe exponentielle. Le modèle est alors qualifié d’exponentiel.
Le temps de doublement d’une population est la durée au bout de laquelle l’effectif de cette population a été multiplié par 2.
Le modèle démographique de Malthus est un modèle de croissance ou de décroissance exponentielle de la population. Il prévoit que, si le taux de mortalité est supérieur au taux de natalité, l’effectif de la population tend vers zéro, et dans le cas contraire, il tend vers l’infini.
Le modèle de Malthus peut s’avérer correct si les taux sont constants, donc plutôt sur des durées courtes de plusieurs années ou dizaines d’années, mais ce modèle n’est pas réaliste à long terme.

Pour bien comprendre :

Fonctions affines, représentations graphiques de droites.
Fonction de variable entière et notation u_n.

1. Modéliser l'évolution d'une population à l'aide des suites numériques

a. Notion de modélisation mathématique

À l’échelle d’un pays ou d’un continent, l’effectif d’une population évolue constamment. Afin d’anticiper les besoins en ressources (eau, nourriture…), il est important de savoir prédire au plus près l’effectif futur d’une population, ainsi que la quantité de ressources qui lui seront nécessaires.

Pour cela, on peut « modéliser », c'est-à-dire partir de données statistiques actuelles sur cette population, et chercher une « traduction » mathématique (formule, équation…) qui les relie le mieux possible. Cette « traduction » mathématique permet ensuite d’effectuer des prévisions.

b. Les suites numériques, un outil pour modéliser

Pour modéliser l’évolution d’une population, on utilise une suite numérique dont la grandeur u évolue en fonction d’une variable n. Comme n ne prend que des valeurs entières positives (0, 1, 2, 3, 4...), u évolue par paliers, on dit que u est une grandeur « discrète ».

Graphiquement, une suite se représente par un nuage de points non reliés. Dans certains cas, ce nuage de points peut être ajusté par une droite (modèle linéaire) ou par une courbe exponentielle (modèle exponentiel).

2. Suite arithmétique et modèle d'évolution linéaire

a. Quelques rappels sur les suites arithmétiques

Une grandeur discrète u varie de manière linéaire en fonction d’un palier entier n, si sa variation absolue [u_n+₁– u_n] est constante.

Remarque
Dire que la variation absolue [u_n+₁– u_n] est constante revient à dire que l’on passe d’un terme u_n au terme suivant u_n+1 en ajoutant toujours la même constante réelle r.

Dans ce cas, la suite de terme général u_n est arithmétique de raison r. L’expression du terme u_n en fonction de n est donné par la relation : u_n = u₀+ nr.

On obtient la représentation graphique suivante en nuage de points, où tous les points de coordonnées (n ; u_n) sont situés sur une droite :

b. Évolution réelle et ajustement par le modèle linéaire

Pour certaines populations, la variation absolue [u_n+₁– u_n] est presque constante d’un palier à l’autre. Les points de la suite représentant l’évolution de la population sont alors presque alignés.
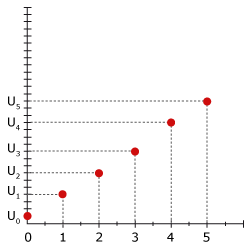
Dans ce cas, on peut ajuster le nuage de points par une droite. Le modèle est alors qualifié de linéaire.

Rappel
Lorsque les points d’un nuage sont presque alignés, il est possible d'« ajuster » ce nuage de points par une droite. Cela revient à déterminer une droite qui passe au voisinage des points.

Une calculatrice ou un tableur permet d’afficher la droite ajustant le nuage de points, et d’en donner une équation.

Méthode pour étudier l’évolution d’une population avec un tableur (Excel), dans le cas d’un modèle linéaire

Ouvrir une feuille de tableur et y saisir :
- en colonne A, l’année ;
- en colonne B, le rang de l’année (de 0 à n) ;
- en colonne C, l’effectif de la population considérée.
À la ligne 1, préciser les titres des trois colonnes.
Sélectionner les deux colonnes. Dans « insertion », cliquer sur « insérer un graphique en nuages de points ». On obtient ainsi une représentation graphique en nuage de points de l’évolution de la population entre les années 0 et n.
Si les points du nuage sont presque alignés, il est pertinent de réaliser un ajustement de ce nuage par une droite. Pour cela, effectuer un clic droit sur l’un des points. Sélectionner « courbe de tendance », « linéaire », et « afficher l’équation ». On obtient la droite d’ajustement et son équation.
Utiliser l’équation de la droite d’ajustement pour effectuer des prévisions.

Exemple

À partir de données fournies sur les six dernières années, on souhaite étudier l’évolution du nombre d’élèves inscrits dans une école. On aimerait également prédire le nombre d’élèves inscrits dans cette école en 2023.

On saisit les données fournies dans une feuille de calcul :
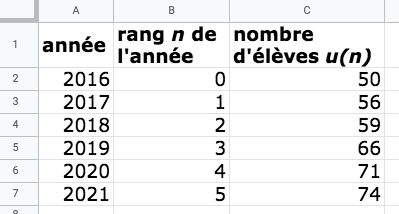
En cliquant sur « insérer un graphique en nuages de points », on obtient la représentation graphique en nuage de points ci-dessous.
Comme les points sont presque alignés, on construit une droite d’ajustement. Cette droite modélise l’évolution de la population :
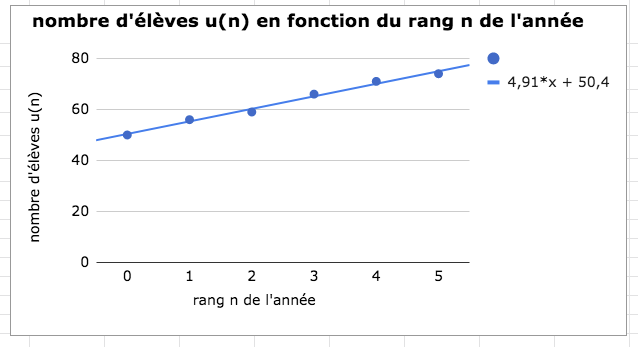
L’année 2023 correspond au rang n = 7 . On calcule donc la valeur de u₇ à partir de l’équation de la droite d’ajustement : u₇ = 4,91 × 7 + 50,4 = 84,77.
D’après ce modèle linéaire, en 2023, on devrait compter environ 85 élèves inscrits dans l’école.

3. Suite géométrique et modèle d'évolution exponentielle

Le modèle linéaire est un modèle mathématique simple. Si la variation absolue [u_n₊₁– u_n] évolue trop fortement entre chaque palier n, ce modèle n’est pas adapté.

a. Quelques rappels sur les suites géométriques

Une grandeur discrète u varie de manière exponentielle en fonction d’un palier entier n, si sa variation absolue [u_n₊₁– u_n] est proportionnelle à u_n.

Remarque
Dire que la variation absolue [u_n₊₁– u_n] est proportionnelle à u_n revient à dire que l’on passe d’un terme u_n au terme suivant u_n₊₁ en multipliant toujours par la même constante réelle q.

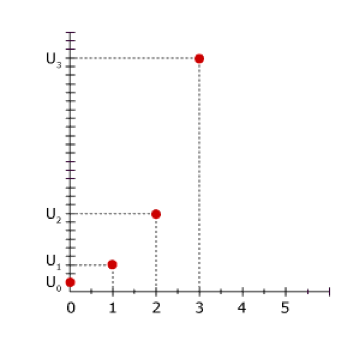
Dans ce cas, sa variation relative (ou taux de variation)

est constante et la suite de terme général u_n est géométrique de raison q = (1 + t). L’expression du terme u_n en fonction de n est donné par la relation : u_n = u₀ × qⁿ.

On obtient la représentation graphique suivante en nuage de points :

b. Évolution réelle et ajustement par le modèle exponentiel

Pour certaines populations, la variation relative

est presque constante d’un palier à l’autre. L’allure du nuage de points représentant l’évolution de la population se rapproche alors d’une courbe exponentielle.
Dans ce cas, on peut ajuster le nuage de points par une courbe exponentielle.
Le modèle est alors qualifié d’exponentiel.

Une calculatrice ou un tableur permet d’afficher la courbe ajustant le nuage de points, et d’en donner une équation.

Méthode pour étudier l’évolution d’une population avec un tableur (Excel), dans le cas d’un modèle exponentiel

Reprendre la première étape de la méthode précédente.
Reprendre la deuxième étape de la méthode précédente.
Si l’allure du nuage de points se rapproche d’une courbe exponentielle, il est pertinent de réaliser un ajustement de ce nuage par une courbe exponentielle. Pour cela, effectuer un clic droit sur l’un des points. Sélectionner « courbe de tendance », « exponentielle », et « afficher l’équation ». On obtient la droite d’ajustement et son équation.
Utiliser l’équation de la courbe d’ajustement pour effectuer des prévisions.

Exemple
À partir de données fournies sur les soixante-dix dernières années, on souhaite étudier l’évolution d’une population. On aimerait également prédire l’effectif de cette population en 2030.

On saisit les données fournies dans une feuille de calcul :
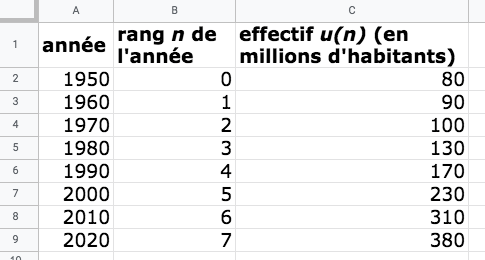
En cliquant sur « insérer un graphique en nuages de points », on obtient la représentation graphique en nuage de points ci-dessous.
Comme l’allure du nuage de points fait penser à une courbe exponentielle, on utilise cette modélisation :
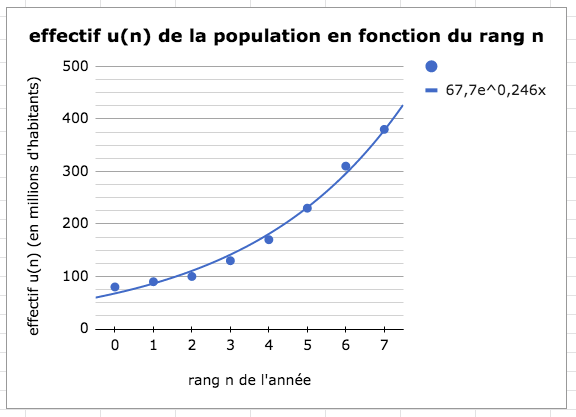
L’année 2030 correspond au rang n = 8 . On calcule donc la valeur de u₈ à partir de l’équation de la courbe d’ajustement : u₈ = 67,7 × e^0,246×8 ≈ 484,5.
D’après ce modèle exponentiel, en 2030 on devrait compter environ 485 millions d’habitants.

c. Détermination du temps de doublement d'une population en croissance exponentielle

Le temps de doublement d’une population est la durée au bout de laquelle l’effectif de cette population a été multiplié par 2.

On note E₁ l’effectif initial d’une population à un instant 1 et E₂ son effectif au bout de n années.On cherche la valeur de n telle que la population a doublé au bout de n années.

Méthode pour obtenir le temps de doublement d’une population par lecture graphique

Cette méthode donne une valeur approximative, moins fiable que celle obtenue par le calcul :

Lire sur l’axe des ordonnées la valeur de l’effectif initial E₁.
Repérer en ordonnée la valeur E₂= 2 × E₁ et chercher en abscisse la valeur n₂ qui lui correspond.
Repérer dans les données l’année correspondant à cette valeur n₂.
Calculer la différence entre l’année correspondant au rang n₂ et celle correspondant au rang 0. Cette différence est égale au temps de doublement.

Exemple
On donne la représentation graphique suivante de l’évolution d’une population :

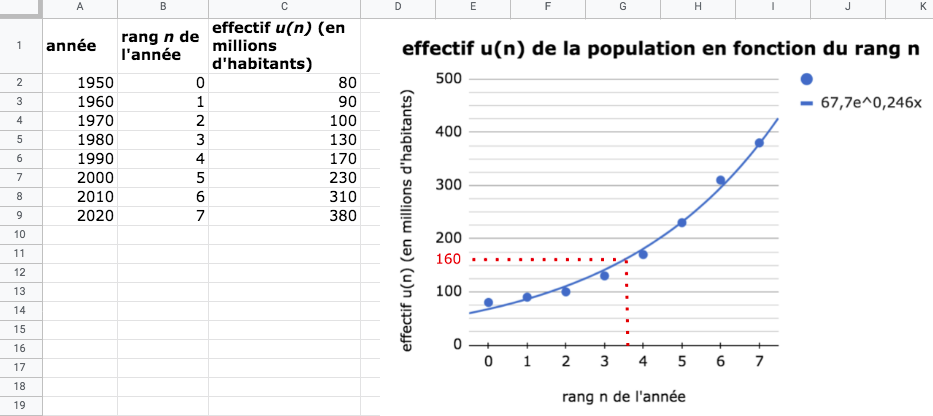
On lit sur l’axe des ordonnées : E₁= 80 millions d’habitants.
Pour E₂= 160, on trouve n ≈ 3,5.
L’année qui correspond à 3,5 est 1985.
Le temps de doublement de la population est donc
1985 – 1950 = 35 ans.

Méthode pour obtenir le temps de doublement d’une population avec un tableur (Excel)

Si l’effectif d’une population augmente de manière exponentielle à un taux annuel t, alors l’effectif E₂ au bout de n années est :
E₂ = E₁ × (1 + t)ⁿ .
On cherche alors le plus petit entier n tel que :

Ouvrir une feuille de tableur et y saisir :
- en colonne A, l’année ;
- en colonne B, le rang de l’année (de 0 à n) ;
- en colonne C, le calcul de (1 + t)ⁿ.
À la ligne 1, préciser les titres des trois colonnes.
En A3, saisir « =A2+1 » et étirer cette cellule vers le bas. En B3, saisir « =B2+1 » et étirer cette cellule vers le bas. En C2, saisir « =1,02^B2 » et étirer cette cellule vers le bas.
Dans le tableau, repérer à partir de quelle année (1 + t)ⁿ devient supérieur à 2.
Calculer la différence entre l’année obtenue en 3 et celle correspondant au rang 0. Cette différence est égale au temps de doublement.

Remarque
Le temps de doublement n ne dépend pas de l’effectif initial, mais uniquement de la valeur du taux d’accroissement t.

Exemple
Soit une population qui croit annuellement de 2 % à partir de l’année 1980 (rang n = 0). Quel est son temps de doublement ?

On cherche donc le plus petit entier n tel que 1,02ⁿ≥ 2. Dans un tableur, on saisit comme suit :
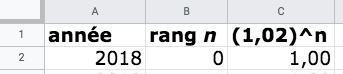
On obtient :
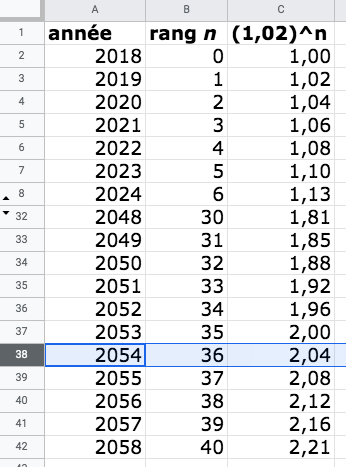
On observe que 1,02ⁿ devient supérieur à 2 à partir de l’année 2054.
Le temps de doublement de la population vaut
2054 – 2018 = 36 ans.

d. Le modèle démographique de Malthus

Thomas Malthus (1766-1834) est un économiste britannique. En 1798, il publie un essai stipulant que lorsque la population n’est arrêtée par aucun obstacle (guerre, famine, épidémie…), elle double tous les 25 ans, donc croît de façon géométrique.

On note t_n le taux annuel de natalité et t_m le taux annuel de mortalité.
Le taux de variation annuel de la population est :

t = t_n – t_m

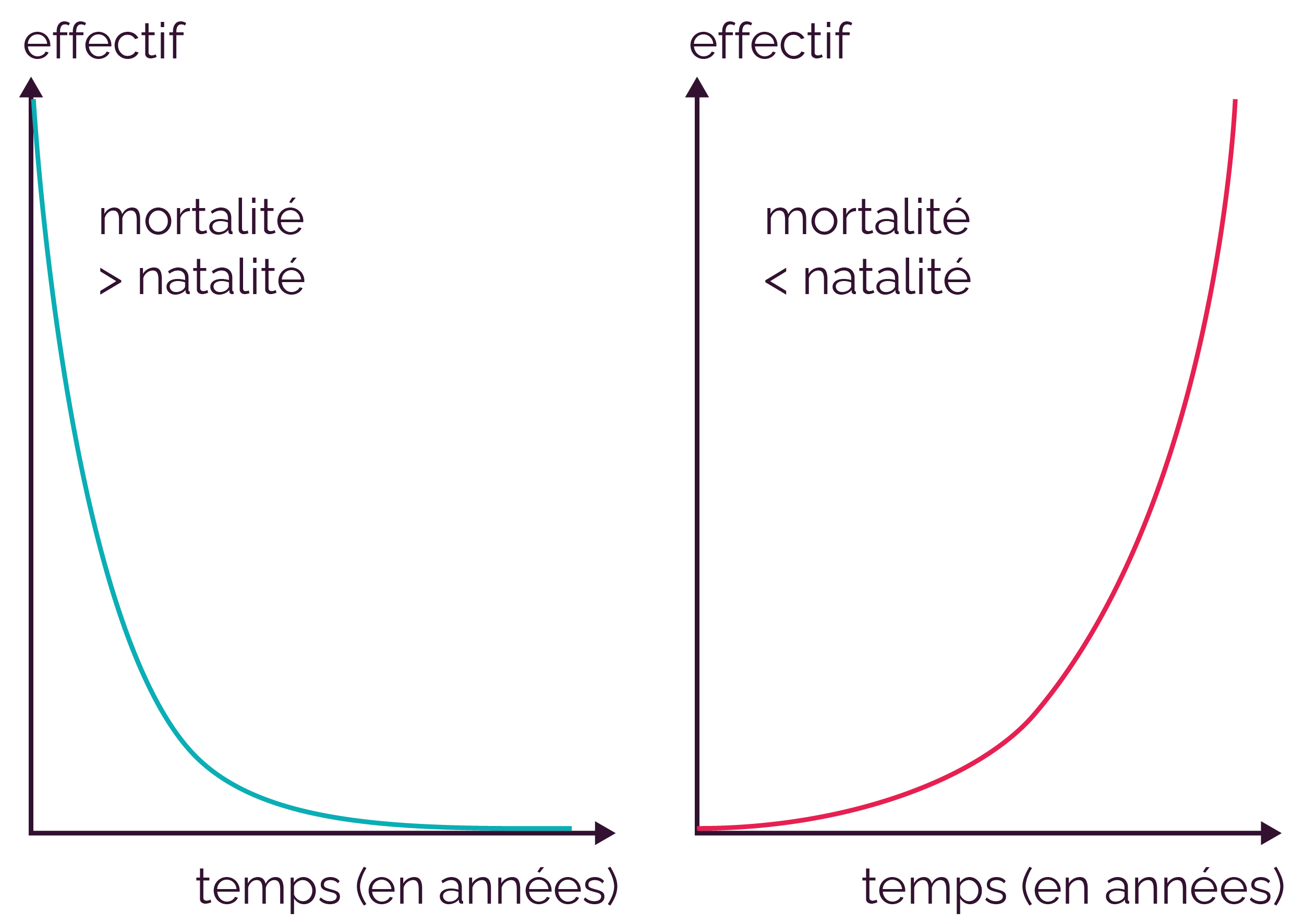
Le modèle démographique de Malthus est un modèle de croissance ou de décroissance exponentielle de la population. Il prévoit que, si le taux de mortalité est supérieur au taux de natalité, l’effectif de la population tend vers zéro, et dans le cas contraire, il tend vers l’infini.

Évolution de l'effectif d'une population selon le modèle de Malthus

Dans le modèle de Malthus, chaque année, l’effectif de la population est multiplié par (1 + t), donc au bout de n années, on peut prédire que l’effectif de la population aura été multiplié par (1 + t)ⁿ .

Exemple
Soit une population de 500 000 habitants en 2020. On observe que depuis une cinquantaine d’années, les taux annuels de natalité et de mortalité ont très peu varié et sont autour de t_n = 12 ‰ et t_m = 9 ‰.
On calcule t : t = t_n – t_m = 0,012 – 0,009 = 0,003.
Et on peut appliquer le modèle de Malthus : on estime qu’après n années, l’effectif de la population sera multiplié par 1,003ⁿ.
Au bout de 40 années, l’effectif de la population sera égal à : effectif final = 500 000 × (1,003)⁴⁰ = 563 647 habitants.

Pour que le modèle de Malthus puisse s’appliquer sur un temps long, il faut une quantité de ressources suffisante pour nourrir la population.

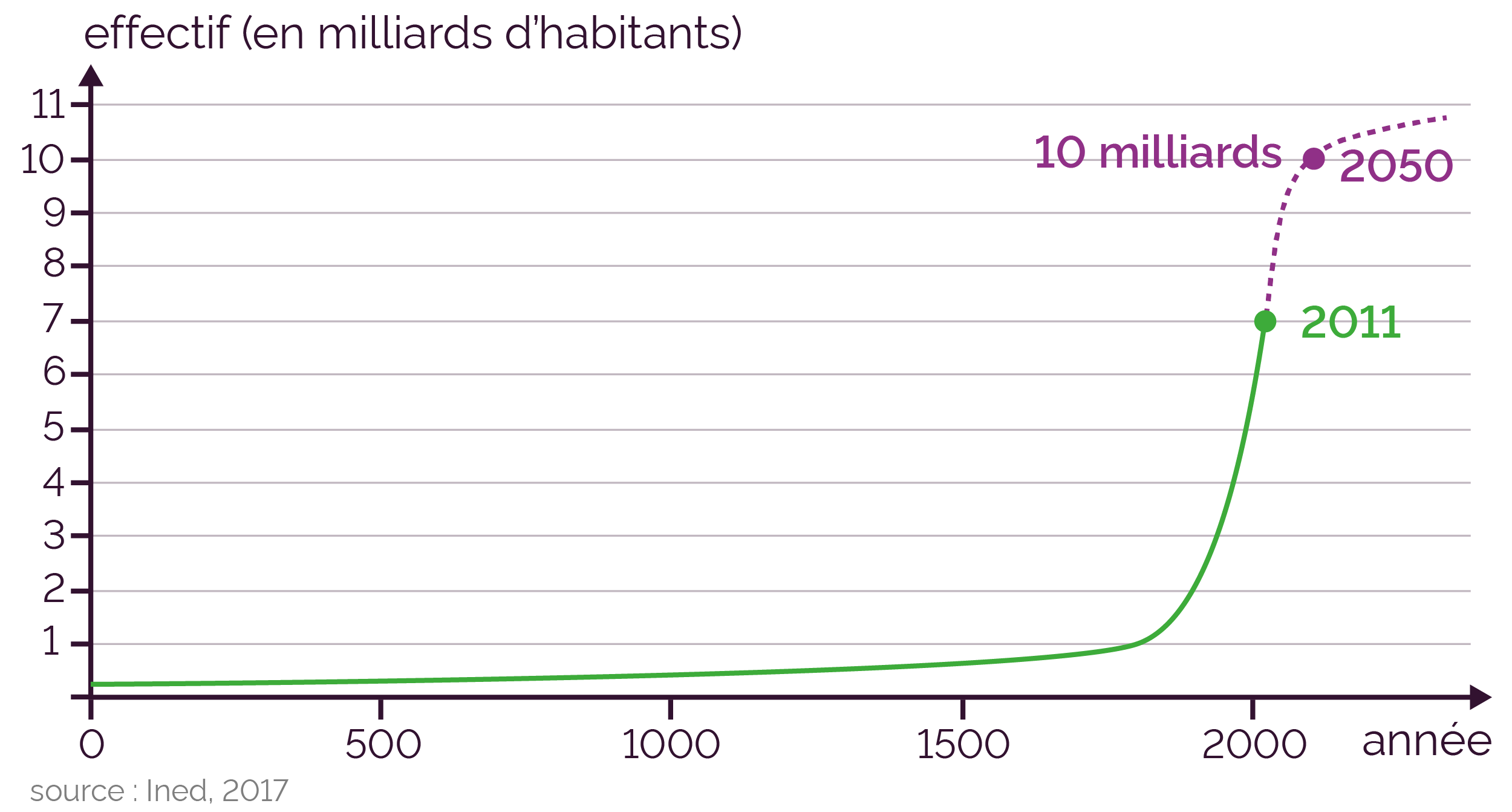
4. La validité du modèle démographique de Malthus

a. L'évolution de la population mondiale depuis la fin du XVIIIe siècle

De la fin du XVIII^e siècle jusqu’à aujourd’hui, on a observé une croissance exponentielle de la population mondiale d’environ 1 % par an :

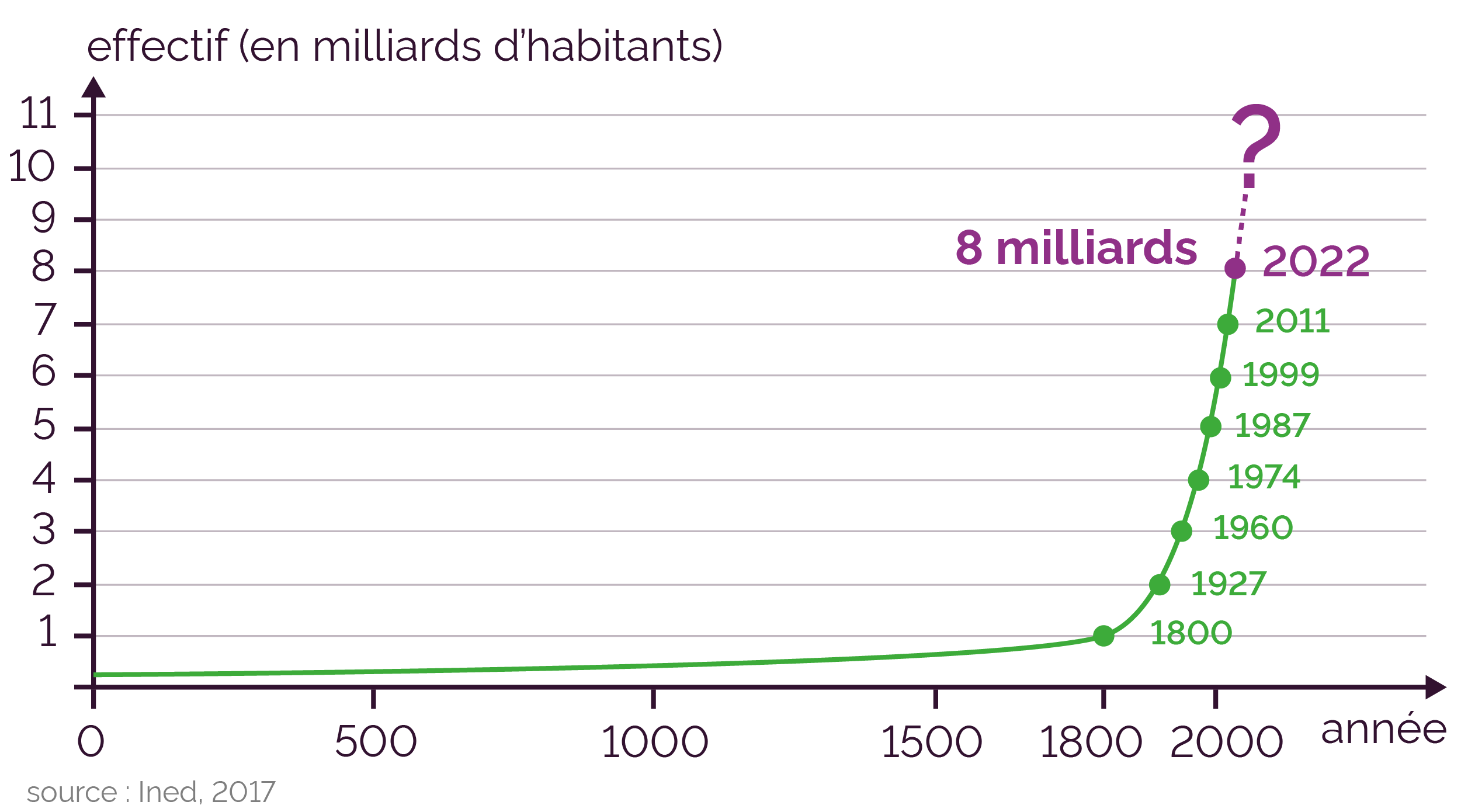
Évolution de la population mondiale

Avec une croissance annuelle de 1 %, le temps de doublement de la population mondiale est de 65 ans.
La population mondiale en 2015 a été estimée à 7,5 milliards d’êtres humains. Si le taux de 1 % se maintient, la population mondiale devrait donc être d’environ 480 milliards en 2405.

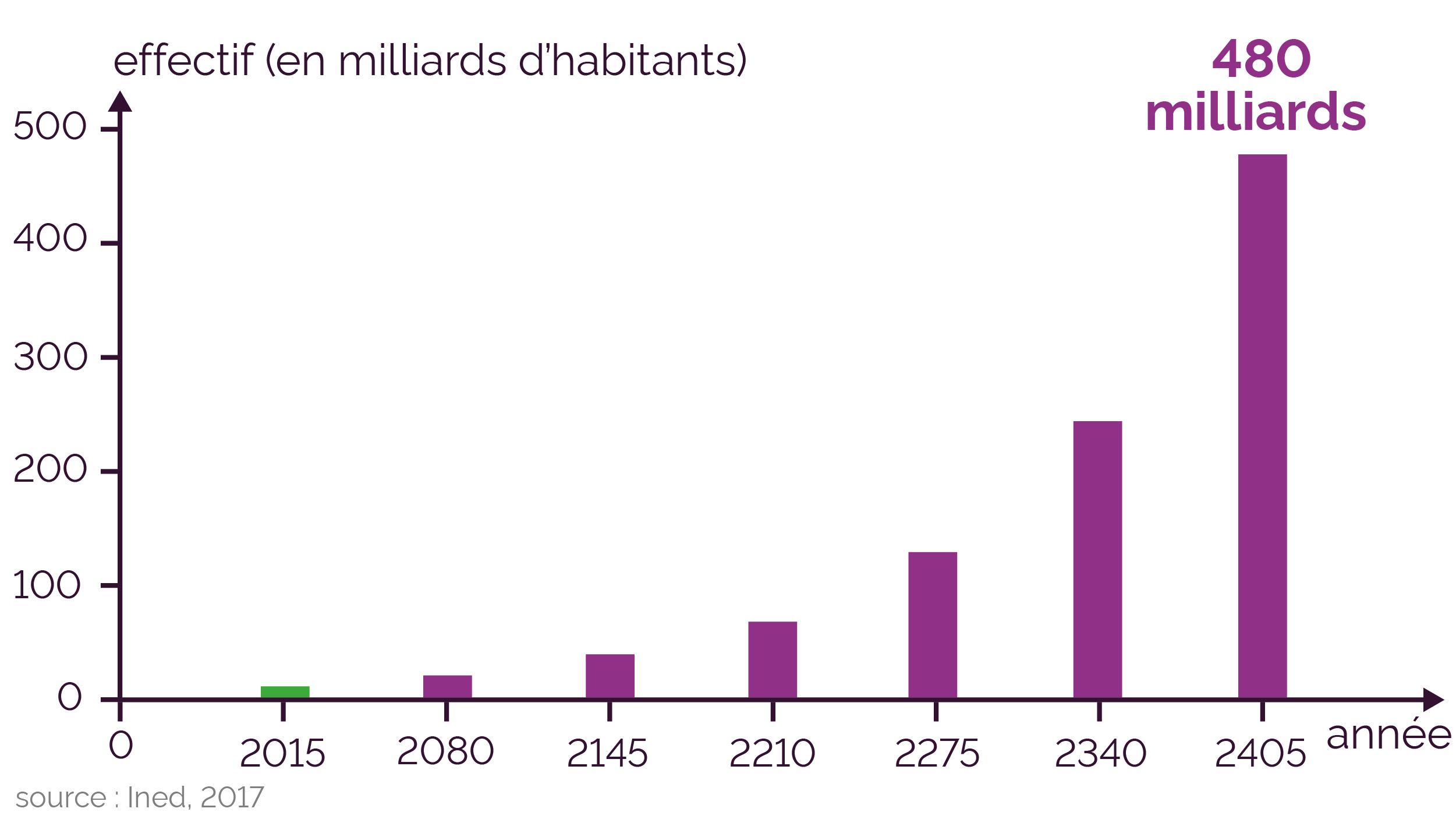
Prévision de l'évolution de la population mondiale,
avec une croissance annuelle de 1 %

Nourrir 480 milliards d’êtres humains demande un certain nombre de ressources disponibles. Or, qu’en est-il de ces ressources ?

b. Comparaison entre une croissance exponentielle et une croissance linéaire

Depuis une soixantaine d’années, on observe que l’évolution de la production mondiale de céréales augmente de manière presque linéaire.

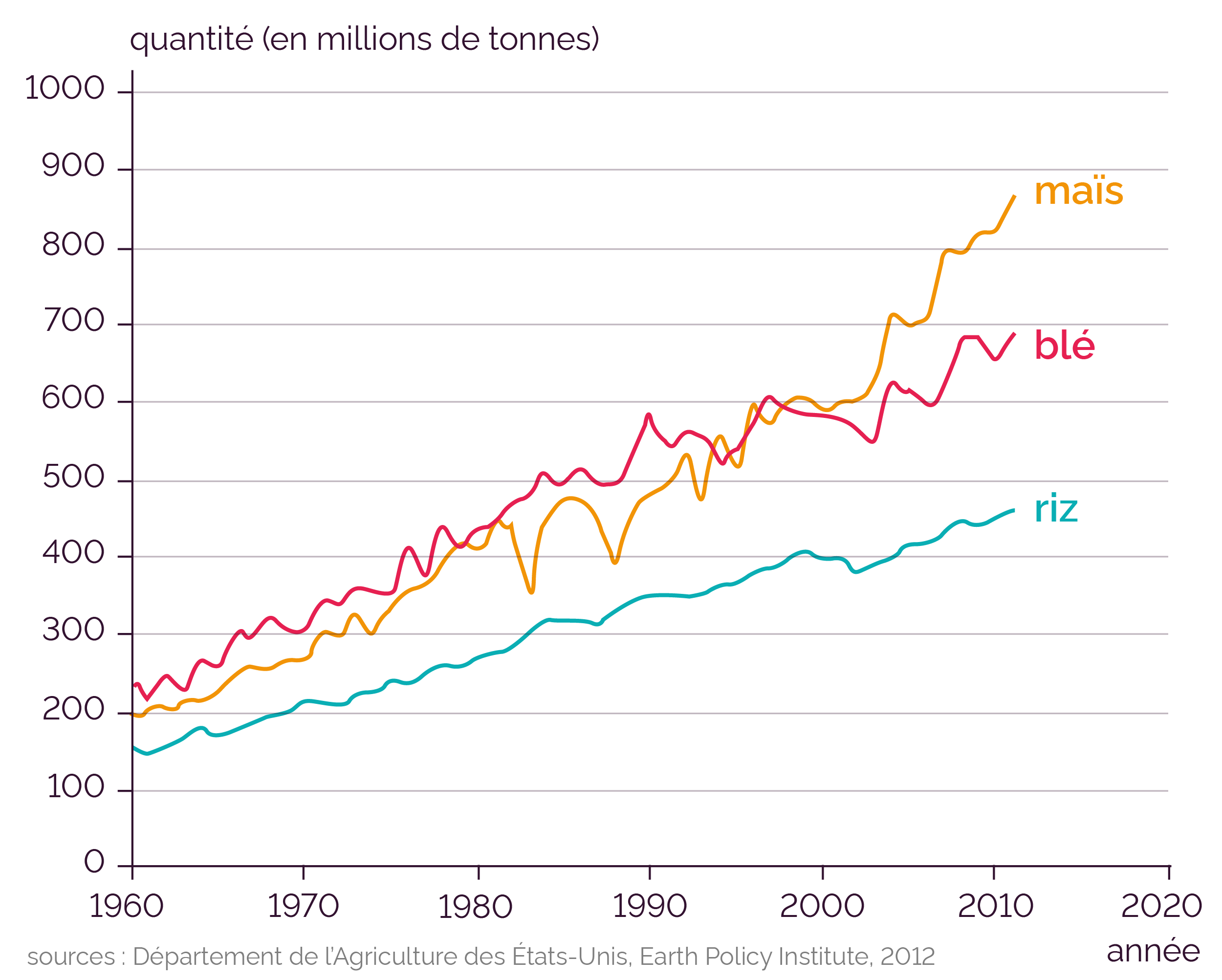
Productions mondiales de maïs, blé et riz entre 1960 et 2011

L’évolution de la production mondiale de céréales peut donc être modélisée par une suite arithmétique.

Si l’effectif d’une population augmente de manière exponentielle alors que la quantité de ressources augmente de manière linéaire, alors à partir d’un certain moment, les deux courbes se croisent. À partir de ce croisement, les ressources ne sont plus suffisantes pour couvrir les besoins de la population.

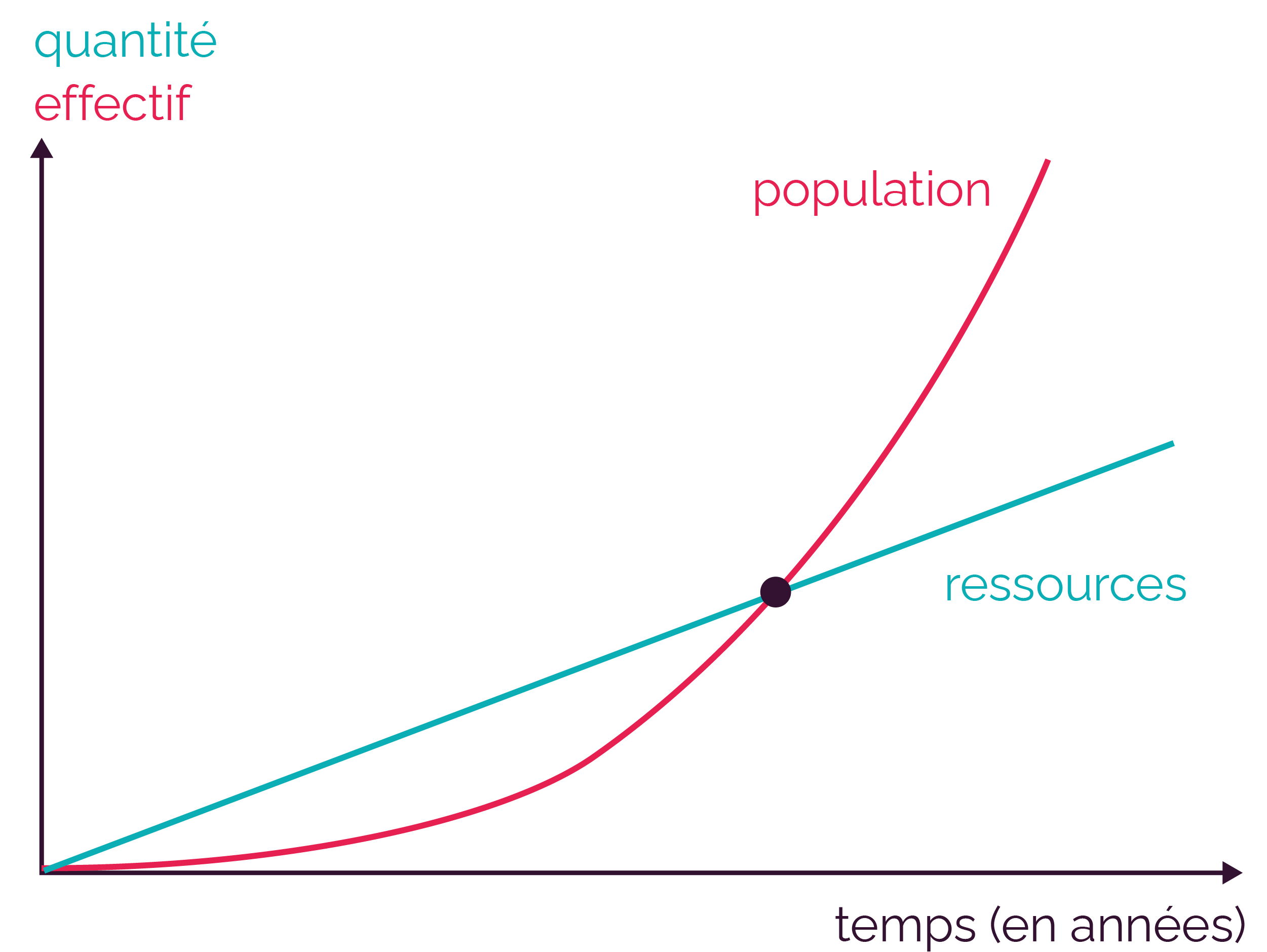
Comparaison entre une croissance exponentielle et une croissance linéaire

Le modèle de Malthus de croissance exponentielle de la population est donc irréaliste à long terme.

Le modèle de Malthus peut s’avérer correct si les taux sont constants, donc plutôt sur des durées courtes de plusieurs années ou dizaines d’années, mais ce modèle n’est pas réaliste à long terme.

c. 10 à 11 milliards d'humains en 2050 ?

De plus, depuis quelques années, le taux de natalité baisse. On observe une stabilisation, voire un fléchissement de certaines populations, en fonction des continents. Par exemple en Europe, la population stagne depuis les années 1990 :

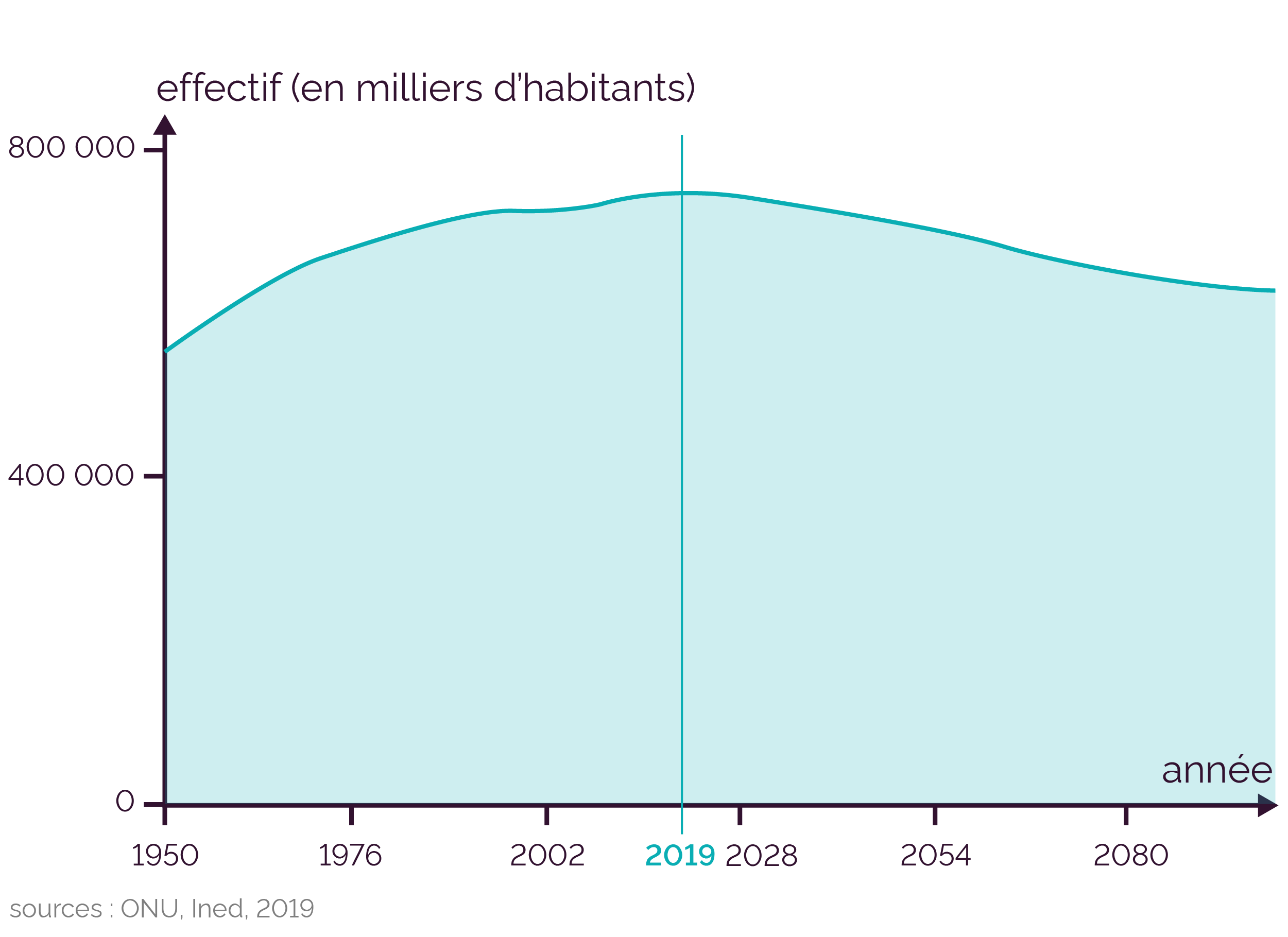
Évolution de la population européenne depuis les années 1950

Les Nations-Unies prévoient une stabilisation d’ici un siècle, avec une population mondiale de 10 à 11 milliards d’habitants en 2050.

Prévision de l'évolution de la population mondiale

Évalue ce cours !

Note 4.3 / 5. Nombre de vote(s) : 66

Des quiz et exercices pour mieux assimiler sa leçon

La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

S’abonner

Des exercices variés pour ne pas s’ennuyer

Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !

Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

S’abonner

Des quiz pour une évaluation en direct

Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.

myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

S’abonner

Des vidéos et des podcasts pour apprendre différemment

Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.

Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

S’abonner

Des podcasts pour les révisions

La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.

Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

S’abonner

Des vidéos de cours pour comprendre en image

Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !

S’abonner

Profs en ligne

Découvrez le soutien scolaire en ligne avec myMaxicours

Plongez dans l'univers de myMaxicours et découvrez une approche innovante du soutien scolaire en ligne, conçue pour captiver et éduquer les élèves de CP à la terminale. Notre plateforme se distingue par une riche sélection de contenus interactifs et ludiques, élaborés pour stimuler la concentration et la motivation à travers des parcours d'apprentissage adaptés à chaque tranche d'âge. Chez myMaxicours, nous croyons en une éducation où chaque élève trouve sa place, progresse à son rythme et développe sa confiance en soi dans un environnement bienveillant.

Profitez d'un accès direct à nos Profs en ligne pour une assistance personnalisée, ou explorez nos exercices et corrigés pour renforcer vos connaissances. Notre assistance scolaire en ligne est conçue pour vous accompagner à chaque étape de votre parcours éducatif, tandis que nos vidéos et fiches de cours offrent des explications claires et concises sur une multitude de sujets. Avec myMaxicours, avancez sereinement sur le chemin de la réussite scolaire, armé des meilleurs outils et du soutien de professionnels dédiés à votre épanouissement académique.

EXERCE-TOI EN T'ABONNANT