L'optimisation du transport de l'électricité
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Identifier l’influence sur l’effet Joule de la puissance, de la résistance, de l’intensité et de la tension.
- Modéliser un réseau de distribution électrique simple par un circuit électrique et par un graphe orienté.
- Formuler le problème de minimisation des pertes par effet Joule et le résoudre pour différentes valeurs numériques.
- Au cours du transport, une partie de l’énergie électrique est dissipée dans l’environnement par effet Joule.
- On limite les pertes par effet Joule en utilisant la haute tension dans les lignes électriques.
- Un réseau de transport électrique peut être modélisé mathématiquement par un circuit électrique ou par un graphe orienté.
- L’objectif est de minimiser les pertes par effet
Joule sur l’ensemble du réseau, avec les
contraintes suivantes.
- L’intensité totale est limitée par la puissance maximale distribuée.
- L’intensité totale qui entre dans chaque nœud est égale à l’intensité totale qui en sort.
- L’intensité totale qui arrive à chaque cible (utilisation) est imposée par la puissance utilisée.
- Notion de graphe
- Connaissances sur les fonctions
On utilise des lignes électriques pour transporter l’énergie électrique qui est produite par les centrales électriques jusqu’aux usagers, parfois sur de longues distances.
En France métropolitaine, il y a environ cent-mille kilomètres de lignes électriques.
Le réseau de transport électrique est complexe : les problèmes de gestion et d’optimisation du transport, ainsi que de la distribution de l’électricité trouvent leurs solutions par des modèles mathématiques (graphes, fonctions, etc.).
Le transport de l’énergie électrique entraine des pertes par effet Joule : les câbles s’échauffent et de l’énergie thermique est dissipée dans l’environnement. Ces pertes représentent un peu plus de 2 % de l’énergie électrique transportée.
Ceci se traduit par un échauffement et donc des pertes d’énergie thermique dans l’environnement : c’est l’effet Joule.
Chaque câble électrique possède une résistance, il subit donc des pertes par effet Joule. Ces pertes sont d’autant plus grandes que les câbles sont longs et que l’intensité du courant est élevée.
La formule suivante établit le lien entre la puissance transportée par le câble, la puissance distribuée et la puissance dissipée par effet Joule.
| Ptransportée = Putile + Peffet Joule |
avec :
|
On voit que toute la puissance ne parvient pas à l’utilisateur.
La puissance électrique (fournie ou reçue) d’un dispositif électrique est donnée par la formule suivante.
| P = U × I |
avec :
|
La puissance dissipée par effet Joule dans un câble électrique est donc la suivante.
| Peffet Joule = Ucâble × I |
avec :
|
La loi d’ohm appliquée au câble électrique est la suivante.
| Ucâble = Rcâble × I |
avec :
|
On en déduit la relation entre la puissance Peffet Joule, la résistance Rcâble et l’intensité du courant I.
Dans un câble électrique, la puissance thermique dissipée par effet Joule est donnée par la relation suivante.
| Peffet Joule = Rcâble × I2 |
avec :
|

Lignes à haute tension
Or, Peffet Joule = Rcâble × I2
Pour diminuer les pertes par effet Joule, donc diminuer la valeur de Peffet Joule, il faut ainsi :
- soit diminuer la résistance des câbles Rcâble : il s’agit d’utiliser des matériaux qui soient de très bons conducteurs ;
- soit diminuer la valeur de l’intensité
du courant I.
On a Ptransportée = U × I, donc I =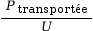 , avec
U la
tension d’alimentation fournie.
, avec
U la
tension d’alimentation fournie.
Pour une valeur de puissance Ptransportée fixe transportée par le câble, la valeur de l’intensité I peut être diminuée en augmentant la tension d’alimentation fournie U.
Des transformateurs sont installés sur le réseau, afin de modifier la valeur d'une tension : ces dispositifs permettent d’augmenter la tension pour limiter les pertes par effet Joule dans les câbles électriques, puis ils permettent de diminuer la tension pour la rendre utilisable par les usagers.

Transformateur
La tension utilisée dans les habitations est de 230 V, celle des lignes à haute tension est d’environ 20 kV et celle des lignes à très haute tension va jusqu’à environ 400 kV.
Voici un schéma qui présente un réseau de transport et de distribution électrique via des lignes à haute tension et des lignes à basse tension.
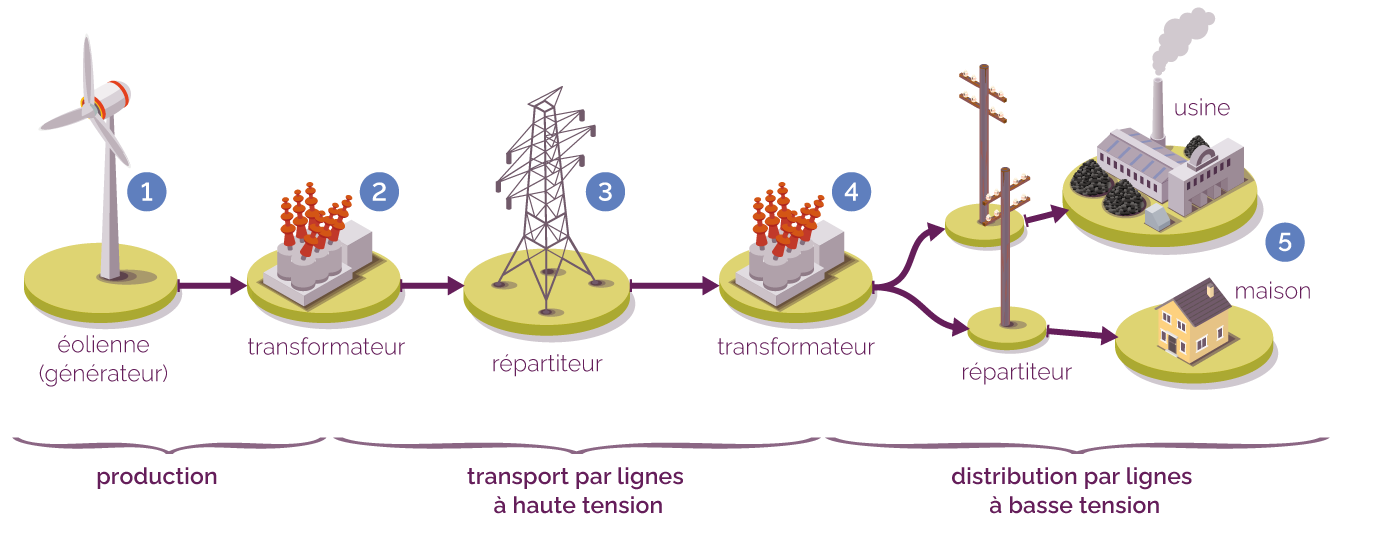
Réseau de transport électrique
Dans ce réseau de transport électrique :
- l’électricité est produite par l’éolienne (générateur) ;
- un transformateur augmente la tension produite par l’éolienne pour obtenir une haute tension.
- cette haute tension est transportée par les lignes à haute tension, en passant par un répartiteur qui va diriger l’électricité à l’échelle régionale ou nationale ;
- un autre transformateur diminue la tension, pour la distribuer à l’échelle locale grâce à des lignes à basse tension ;
- l’énergie est utilisée par les différents usagers.
Voici un circuit électrique qui permet de modéliser le transport de l’électricité de ce réseau grâce aux lignes électriques.
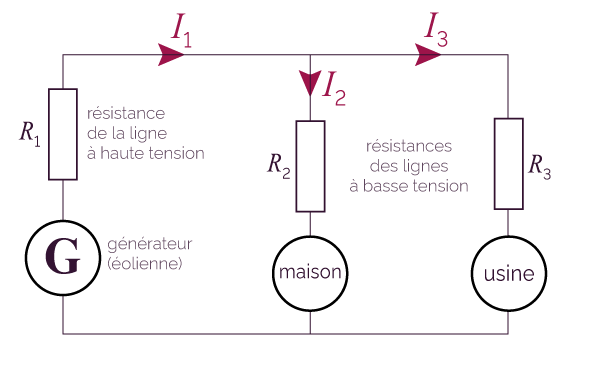
Modélisation du réseau de transport électrique
par un circuit électrique
Un réseau de transport électrique peut être modélisé par un graphe orienté, très utile pour résoudre mathématiquement le problème de minimisation des pertes par effet Joule.
On souhaite modéliser un réseau de transport électrique constitué :
- d’une éolienne et un panneau photovoltaïque, qui sont les deux sources d’énergie électrique ;
- d’un répartiteur pour ajuster la production en fonction des besoins ;
- d’une maison et une usine, qui sont les deux cibles utilisatrices de l’électricité ;
- de quatre câbles électriques pour le transport.
Voici un schéma de ce réseau de transport électrique.
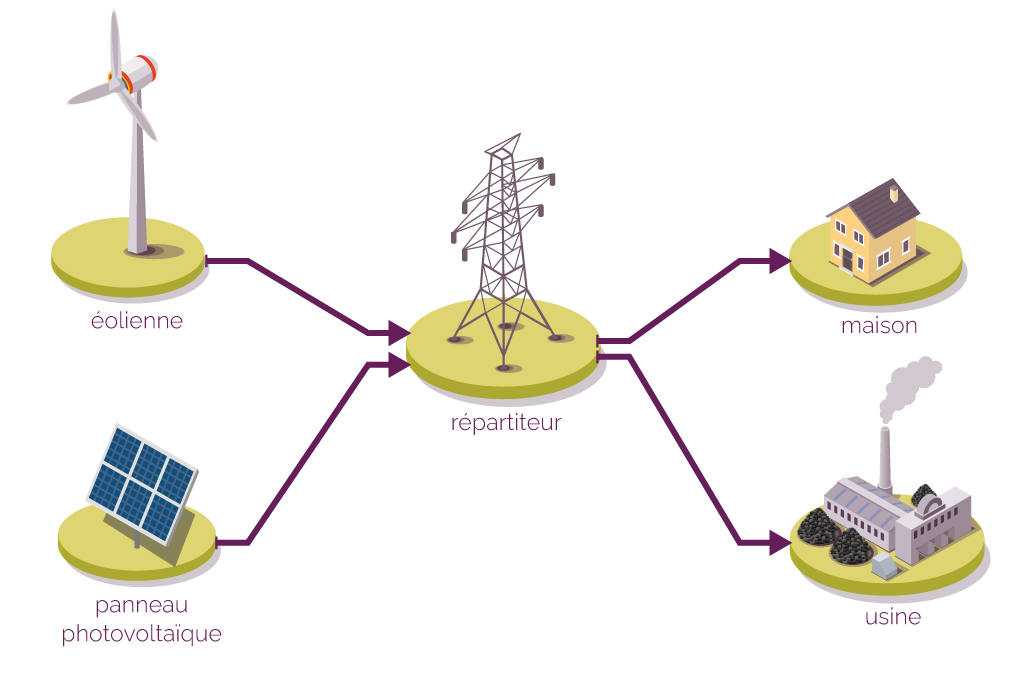
Schéma du réseau de transport électrique
Voici une modélisation de ce réseau de transport électrique par un circuit électrique.
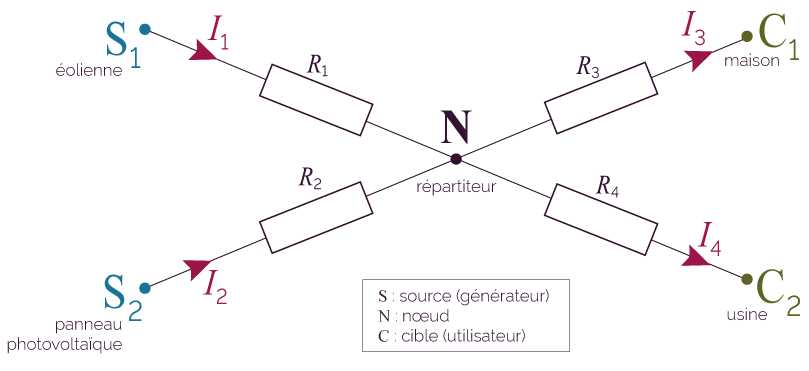
Modélisation du réseau de transport électrique
par un circuit électrique
- Les sources S1 et S2 représentent les générateurs d’énergie électrique (éolienne et panneau photovoltaïque ici).
- Les cibles C1 et C2 représentent les utilisateurs d’énergie électrique (maison et usine ici).
- R1, R2, R3 et R4 sont les résistances des câbles électriques.
- I1, I2, I3 et I4 sont les intensités des courants qui circulent dans les câbles électriques.
- Le point N au milieu s’appelle le nœud : il représente le répartiteur du circuit.
Voici une modélisation du réseau de transport électrique par un graphe orienté.
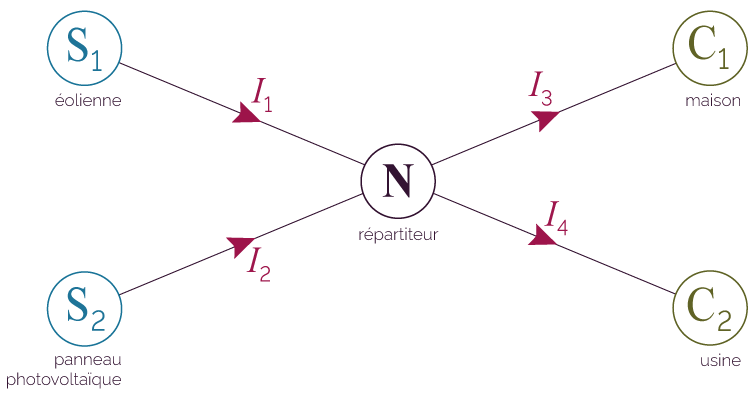
Modélisation du réseau de transport électrique
par un graphe orienté
- Les lignes électriques sont représentées par des arcs (segments) orientés dans le sens du courant.
- Les sources S1 et S2, et les cibles C1 et C2 sont situées aux sommets de ces arcs.
L’étude du graphe orienté et la connaissance des contraintes d’un réseau de transport électrique, permettent de minimiser les pertes par effet Joule en résolvant le problème mathématique associé.
- Puissance dissipée par effet Joule : Peffet Joule = R × I2
- La puissance totale dissipée par effet Joule sur l’ensemble d’un réseau est la somme de toutes les puissances dissipées par effet Joule : Ptotale effet Joule = Peffet Joule 1 + Peffet Joule 2 + … + Peffet Joule 5 + …
- Puissance d’un dispositif : P = U × I
Un réseau de transport électrique doit respecter trois contraintes pour répartir l’intensité.
Chaque source fournit une puissance variable, en
fonction des besoins, mais possède une
capacité de puissance maximale Pmax.
La tension U est de plus constante
à ses bornes.
L’intensité qui en sort est donc variable mais elle est inférieure à l’intensité maximale possible Imax.
Une centrale nucléaire possède une capacité de puissance maximale égale à 500 MW et une tension en sortie égale à 90 kV.
L’intensité maximale Imax qui peut sortir de cette centrale est donc égale à :
Imax = ![]() = 5,6 × 103 A
= 5,6 × 103 A
Si I1 et I2 arrivent à un nœud et que I3 et I4 repartent du nœud, alors :
I1 + I2 = I3 + I4
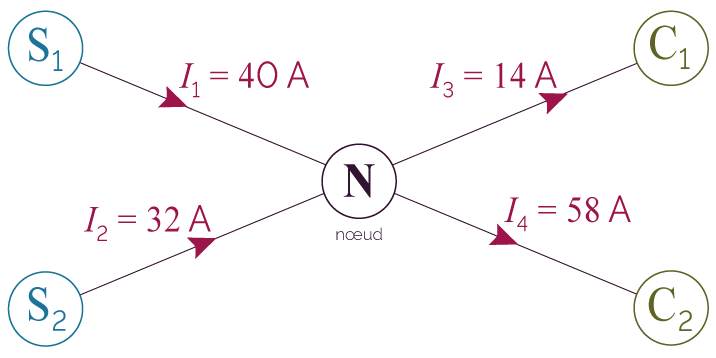
Chaque usager utilise une intensité dont la valeur dépend de son abonnement de puissance électrique. La tension d’utilisation étant constante, l’intensité utilisée possède donc une valeur fixe.
Si une maison possède un abonnement pour une puissance de 12 kW et fonctionne sous une tension de 230 V, alors l’intensité utilisée est égale à :
I = ![]() = 52,2 A
= 52,2 A
Minimiser les pertes par effet Joule sur un réseau de transport électrique consiste à réduire la valeur de la puissance dissipée par effet Joule Peffet Joule.
Voici la méthode à suivre.
Étape 1 – Modéliser le réseau de transport électrique par un graphe orienté.
Étape 2 – Établir l’expression mathématique des trois contraintes du réseau de transport électrique.
Étape 3 – Établir la fonction qui permet d’exprimer la puissance totale dissipée par effet Joule Peffet Joule pendant le transport, en fonction de l’intensité.
Étape 4 – Déterminer le minimum de la fonction polynôme du second degré obtenue, à partir d’un graphique fourni, ou à l’aide d’une calculatrice ou d’un logiciel.
Les intensités des courants qui arrivent aux cibles sont fixées par les besoins des cibles, il ne s’agit donc pas de variables qu’on peut minimiser.
Seules les intensités issues des sources peuvent être minimisées.
On étudie un réseau de transport électrique qui est constitué de deux sources d’énergie électrique (S1 et S2), de quatre câbles, d’un nœud de répartition (N) et de deux cibles utilisatrices (C1 et C2).
- Source 1 :
- Puissance maximum
délivrée :
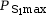 = 18 000 W
= 18 000 W
- Tension à ses
bornes :
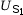 = 360 V
= 360 V
- Puissance maximum
délivrée :
- Source 2 :
- Puissance maximum
délivrée :
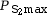 = 10 000 W
= 10 000 W
- Tension à ses
bornes :
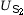 = 260 V
= 260 V
- Puissance maximum
délivrée :
- Résistances des câbles : R1 = 0,8 Ω ; R2 = 0,6 Ω ; R3 = R4 = 1 Ω
- Les cibles fonctionnent chacune sous une puissance P = 6000 W et sous une tension U = 230 V.
Étape 1 – On modélise le réseau de transport électrique par le graphe orienté suivant.
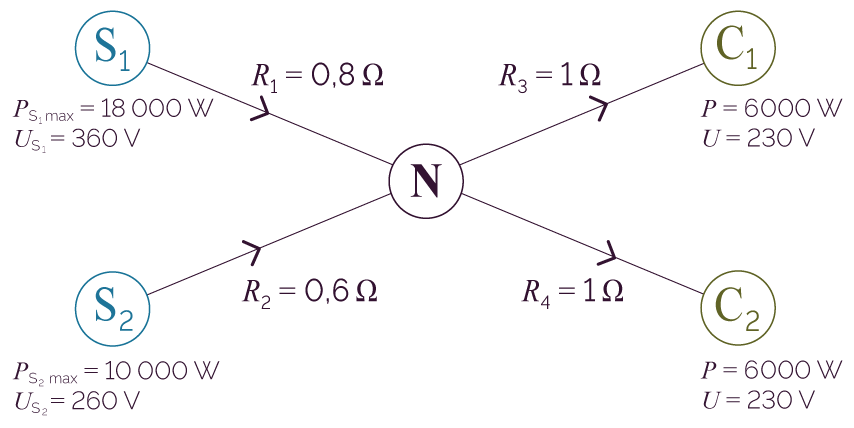
Étape 2 – On établit l’expression mathématique des trois contraintes.
- L’intensité totale qui sort
d’une source est limitée par la puissance
maximale distribuée par cette source :
donc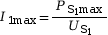
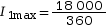 = 50 A
= 50 A
donc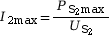
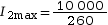 = 38,5 A
= 38,5 A
- L’intensité totale qui entre dans
chaque nœud intermédiaire est égale
à l’intensité totale qui en
sort.
I1 + I2 = I3 + I4
I2 = I3 + I4 – I1 - L’intensité qui arrive à chaque
cible est imposée par la puissance qui y est
utilisée. On obtient :
I3 = I4 =
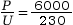 = 26,1 A
= 26,1 A
Étape 3 – Il faut ensuite exprimer la puissance totale dissipée pendant le transport par effet joule Peffet Joule, en fonction de l’intensité de l’une des sources. On prend I1.
Peffet Joule = Peffet Joule 1 + Peffet Joule 2 + Peffet Joule 3 + Peffet Joule 4
Peffet Joule = R1 × I12 + R2 × I22 + R3 × I32 + R4 × I42
Peffet Joule = 0,8 × I12 + 0,6 × I22 + 1 × 26,12 + 1 × 26,12
Peffet Joule = 0,8 × I12 + 0,6 × I22 + 1362
or, I2 = I3 + I4 – I1 = 26,1 + 26,1 – I1 = 52,2 – I1
On obtient :
Peffet Joule = 0,8 × I12 + 0,6 × (52,2 – I1)2 + 1362
Peffet Joule = 0,8 × I12 + 0,6 × (52,22 – 2 × 52,2 × I1 + I12) + 1362
Peffet Joule = 0,8 I12 + 1635 – 62,6 × I1 + 0,6 I12 + 1362
Peffet Joule = 1,4 I12 – 62,6 I1 + 2997
On obtient une fonction polynôme du second
degré, du type :
f(x) = ax2 + bx + c,
qui comporte un minimum (car a = 1,4 est un nombre
positif).
Étape 4 – On peut déterminer le minimum en rentrant la fonction dans une calculatrice ou un logiciel.
La courbe représentative de la fonction obtenue est une parabole du type :
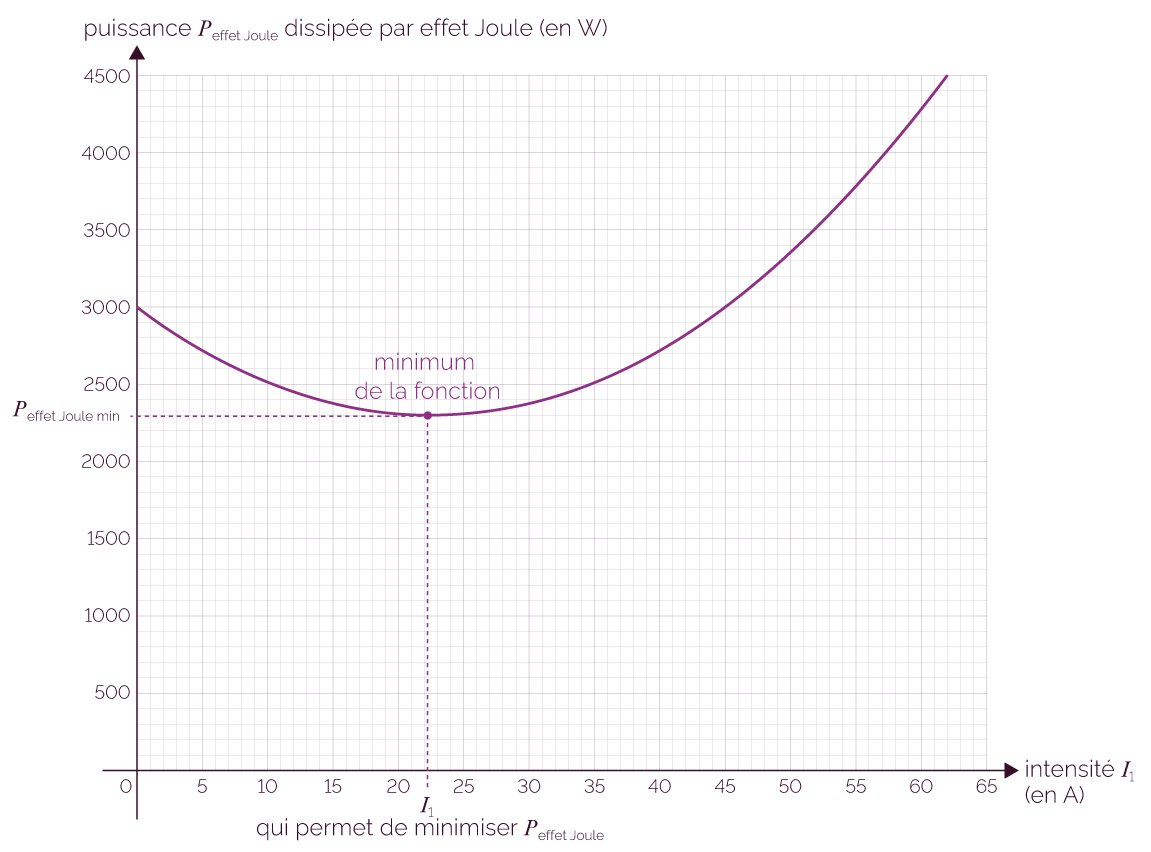
Courbe représentative de Peffet Joule en fonction de I1
On trouve graphiquement que Peffet Joule atteint son minimum pour I1 = 22,3 A.
Les pertes par effet Joule de ce réseau peuvent être minimisées en utilisant cette valeur d’intensité I1 = 22,3 A.
- On a exprimé Peffet Joule en fonction de I1, mais on pourrait également exprimer Peffet Joule en fonction de I2.
- Les exemples étudiés dans ce chapitre sont très simplifiés : l’intensité est par exemple considérée continue, alors qu’en réalité elle est alternative.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !









