Lycée > Premiere > Physique Chimie > Estimer le pouvoir calorifique massique d'une combustion

Estimer le pouvoir calorifique massique d'une combustion

Fiche de cours
Quiz
Profs en ligne
Videos
Application mobile

Objectif

Mettre en œuvre une expérience pour estimer le pouvoir calorifique massique d’un combustible.

Points clés

Il faut effectuer un bilan d’énergie entre tous les constituants de la réaction pour calculer l’énergie libérée par un combustible.
Il faut tenir compte de la masse de combustible qui a subi la combustion pour en déduire le pouvoir calorifique massique permettant d’obtenir la chaleur de combustion.
Le pouvoir calorifique massique PC d’une combustion est l’énergie E que l’on peut récupérer lorsque 1 kg de combustible réagit complètement avec le dioxygène de l’air. Il s’exprime par :
.

Pour bien comprendre

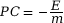Équation de la réaction de combustion
Coefficients stœchiométriques

1. Le pouvoir calorifique d'un combustible

a. Définition

Le pouvoir calorifique massique d’une combustion (ou pouvoir calorifique) est l’énergie que l’on peut récupérer (sous forme de chaleur) lorsque 1 kg de combustible réagit complètement avec le dioxygène de l’air.
Il se note PC et s’exprime en kilojoule par kilogramme (kJ·kg⁻¹).

Le pouvoir calorifique correspond à une énergie E libérée par kilogramme de combustible.

La réaction étant exothermique (elle dégage de la chaleur), le pouvoir calorifique est une grandeur négative.

Remarque
D’autres unités pour le PC sont possibles, telles que J·kg⁻¹, MJ·kg⁻¹, etc.

b. Calculer le pouvoir calorifique massique d'un combustible

Le pouvoir calorifique massique s’exprime par la relation suivante.

avec :

PC le pouvoir calorifique, en joule par kilogramme (J·kg⁻¹)
E la chaleur libérée lors de la combustion, en joule (J)
m la masse de combustible qui subit la combustion, en kilogramme (kg)

Le signe « − » signifie qu’il y a une perte d’énergie du système suite à sa combustion : l’énergie E est négative car elle est libérée par le système. Le pouvoir calorifique est quant à lui positif.

Exemple
La combustion d’un morceau de sucre de 5,0 g libère 49,4 kJ.
Le pouvoir calorifique de cette combustion est alors

, avec E = −49,4 kJ et m = 5,0 g = 5,0 × 10⁻³ kg.

On a donc :

PC = 9,9 × 10³ kJ·kg⁻¹.

2. Expérience

a. Principe

On souhaite ici déterminer le pouvoir calorifique PC de combustion (aussi appelé chaleur de réaction) de la paraffine, de formule brute C₂₅H₅₂, contenue dans une bougie.

La réaction de combustion de la paraffine s’écrit :

C₂₅H₅₂(s) + 38 O₂(g) → 25 CO₂(g) + 26 H₂O(l)

Il faut pour cela chauffer un récipient rempli d’eau grâce à la réaction de combustion (exothermique) de la paraffine contenue dans une bougie.

b. Matériel utilisé

Le montage pour calculer le pouvoir calorifique massique de la paraffine nécessite l’utilisation du matériel de chimie suivant.

1 potence
1 pince
1 noix
1 thermomètre
1 canette
1 bougie

1 soucoupe
Des allumettes
De l’eau distillée
1 éprouvette graduée
1 agitateur en verre

c. Protocole expérimental

On utilise le protocole suivant.

Peser la canette et la fixer sur la potence.
On pèse la canette et on note sa valeur : m_can = 14,5 g.
À l’aide d’une pince, on attache la canette vide à la potence.
Introduire l’eau dans la canette.
On introduit m = 200 g d’eau (soit 200 mL mesurés à l’aide d’une éprouvette graduée) dans la canette.
Relever la température initiale de l’eau.
On plonge un thermomètre dans la canette et on relève la température dans l’eau : θ₁ = 10 °C.
Peser la bougie et son support et la placer sous la canette.
On place une bougie sur une soucoupe et on pèse la masse de l’ensemble : m₁ = 35 g (cette valeur est à adapter selon le matériel utilisé).
On place ensuite la bougie de sorte que celle-ci soit à environ 3 cm du fond de la canette.
Allumer la bougie.
On allume la bougie et on agite continuellement l’eau contenue dans le récipient à l’aide d’une baguette en verre pour homogénéiser la température.

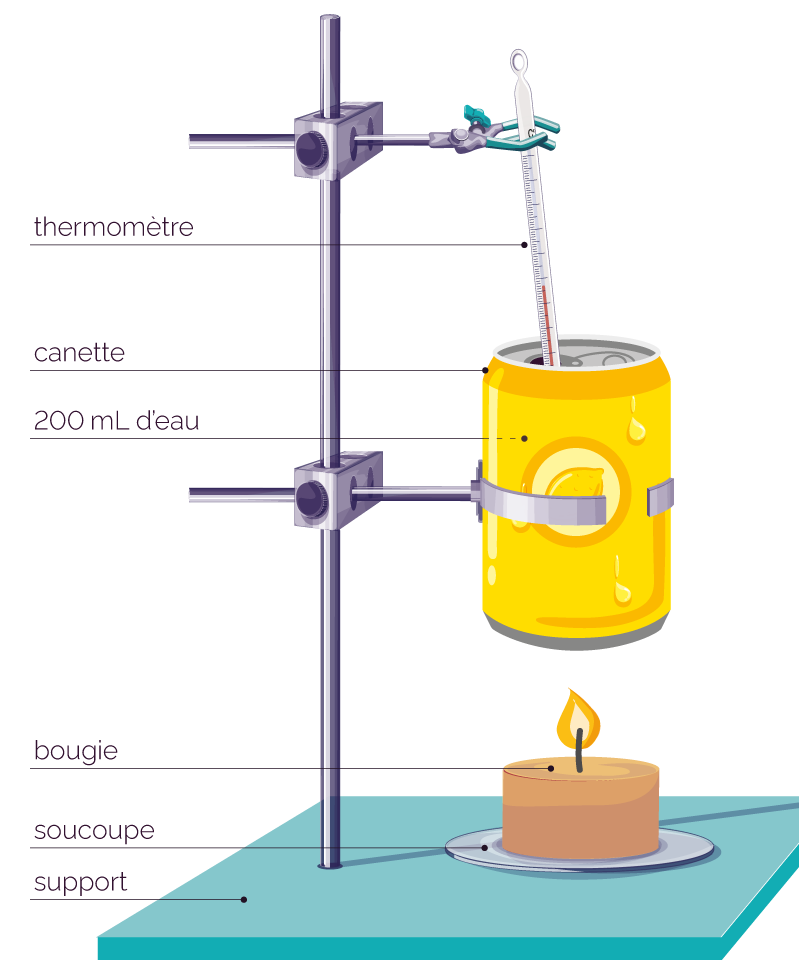
Schéma du montage
Éteindre la bougie et relever la température finale de l’eau.
Lorsque la température a augmenté de 10 °C, on éteint la bougie pour arrêter la combustion et on note la température finale de l’eau contenue dans la canette : θ₂ = 20 °C.
Peser la bougie et son support.
On pèse l’ensemble {bougie + coupelle} et on obtient m₂ = 34,9 g.

3. Exploitation des résultats

a. Calcul du pouvoir calorifique

Calcul de l’énergie libérée par la bougie

On suppose que l’énergie libérée par la combustion de la bougie E_bougie est entièrement utilisée pour chauffer l’eau et le métal qui constitue la canette (il n’y a pas de pertes vers l’extérieur). L’eau a alors emmagasiné l’énergie E_eau et la canette l’énergie E_canette pour élever chacune leur température. La bougie a perdu de l’énergie pour chauffer l’eau et la canette.

On peut donc écrire : E_bougie = −(E_canette + E_eau).

On sait que la chaleur emmagasinée E par un élément s’exprime ainsi.

avec :

c la capacité thermique massique du matériau qui constitue l’élément, en joule par gramme par degré Kelvin (J·g⁻¹·K⁻¹)
m la masse de l’élément, en gramme (g)
θ_f la température finale de l’élément, en degré Kelvin (K)
θ_i la température initiale de l’élément, en degré Kelvin (K)

Remarques

La formule 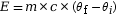n’est pas à connaitre.
c est l’énergie nécessaire pour augmenter la température de 1 g d’un corps de 1 degré Kelvin (K).

On a donc :

E_can = m_can × c_can × (θ_f − θ_i) avec c_can = 0,90 J·g⁻¹·K⁻¹ et (θ_f − θ_i) = 10 °C = 283 K car la température a augmenté de 10 °C au cours de l’expérience.
E_eau = m_eau × c_eau × (θ_f − θ_i) avec c_eau = 4,187 J·g⁻¹·K⁻¹ et (θ_f − θ_i) = 10 °C = 283 K car la température a augmenté de 10 °C au cours de l’expérience.

On en déduit donc l’énergie libérée par la bougie :
E_bougie = −(E_canette + E_eau)

soit :
E_bougie = −(m_can × c_can × (θ_f − θ_i) + m_eau × c_eau × (θ_f − θ_i))
E_bougie = −(14,5 × 0,90 × 283 + 0,2 × 4,187 × 283)
E_bougie = −3,93 kJ = −3,93 × 10³ J

Calcul du pouvoir calorifique de la bougie

Après avoir déterminé l’énergie libérée par la bougie lors de sa combustion, on peut calculer le pouvoir calorifique PC de la bougie en utilisant la formule suivante.

avec :

PC_bougie le pouvoir calorifique de la bougie
E_bougie l’énergie libérée (sous forme de chaleur) par la bougie
m_bougie la masse de bougie qui a subi la combustion

La masse m de bougie qui a subi la combustion est m = m₁ − m₂ = 35 − 34,9 = 0,1 g.

On a donc kJ·g⁻¹.

b. Calcul de l'écart relatif et conclusion de l'expérience

L’écart relatif d’une grandeur X se mesure par rapport à une valeur de référence.

Il sert à comparer la valeur trouvée suite à une expérience à la valeur théorique de référence pour valider les résultats.
Il se note e et s’exprime par :

L’écart relatif n’a pas d’unité et peut s’exprimer en %.

En général, lorsque sa valeur est inférieure à 5 %, on conclut que l’expérience s’est déroulée correctement et que la valeur trouvée est proche de la valeur attendue.

Le pouvoir calorifique théorique de la paraffine est PC_théorique = 40,0 kJ·g⁻¹.

Remarque
Cela signifie que l’énergie qui peut être récupérée lors de la combustion de 1 kg de paraffine est en théorie de Q = 40,0 kJ·g⁻¹.

On calcule l’écart relatif e entre ces 2 mesures :

soit 2 %.

La valeur trouvée expérimentalement est proche de la valeur théorique mais il subsiste tout de même une différence.

Cette différence peut s’expliquer par quelques paramètres d’erreurs dont il faut tenir compte :

les fuites thermiques sont des pertes énergétiques non prises en compte ici puisque la bougie allumée ne chauffe pas que la canette et l’eau : une partie de sa chaleur est « perdue » en chauffant l’air ambiant ;
la masse m de la bougie ne contient pas 100 % de paraffine : d’autres constituants de la bougie ont peut-être subi d’autres réactions de combustion parasites ;
l’homogénéisation de la température a peut-être été insuffisante.