Champ gravitationnel et champ de pesanteur
- Fiche de cours
-
Quiz et exercices
1
- Vidéos et podcasts
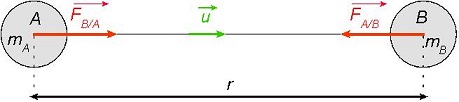
La loi de la gravitation s’applique pour des corps ponctuels, ou pour des corps à symétrie sphérique. Dans ce dernier cas, la masse du corps est exprimée au niveau de son centre de d'inertie. En première approximation, cette hypothèse est validée pour les objets célestes comme les planètes où les étoiles.
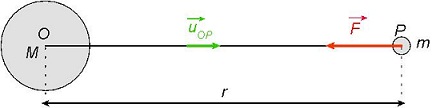
La force
Comme une force s’exprime en Newton et une masse en kilogramme, on en déduit que le champ de gravitation est en
Le champ de gravitation ne dépend pas de la masse m qui subit ce champ, mais de la masse M qui le créé. On peut voir qu’une unité équivalente de
Graphiquement,
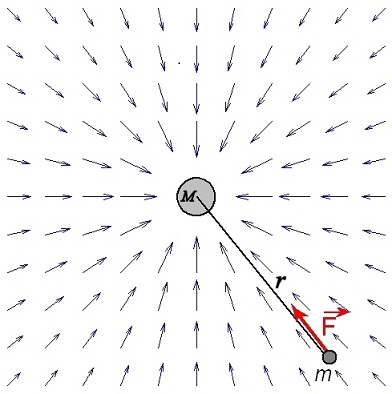
Le vecteur
On vient de fabriquer un gravimètre. Cet écartement est constant, on en déduit que le champ de pesanteur
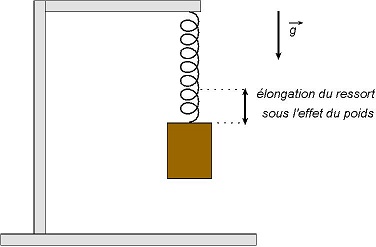
Localement, le champ de gravitation
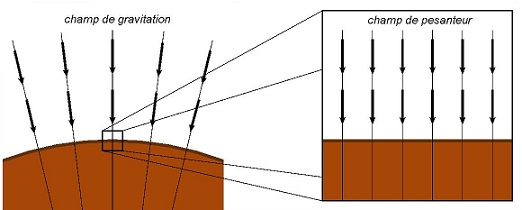
Cela implique que localement,
On identifie l’intensité de pesanteur g comme :
Le champ de gravitation est établi exclusivement par la loi de la gravitation universelle.
Le champ de pesanteur est un champ que l’on peut le mesurer directement via notre gravimètre. Il inclut bien entendu la gravitation, mais aussi le fait que la Terre tourne sur elle-même, ce qui entraîne l’apparition d’une pseudo-force centrifuge, comme celle que l’on ressent dans une voiture prenant un virage à grande vitesse (on est « attiré » vers l’extérieur du virage).
Une conséquence de cela est que la verticale en un lieu, définie par le gravimètre ou un fils à plomb, n’est pas exactement dirigée vers le centre de la Terre. Ainsi, les champs de gravitation et de pesanteur présentent localement des lignes de champ très similaires, mais qui ne sont pas strictement confondues en toute rigueur.
Pour assurer l’égalité
Après, on écrit :
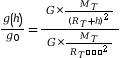 et finalement :
et finalement : Pour
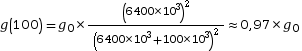 .
.Autrement dit, à 100 km d’altitude, l’intensité de pesanteur n’a chuté que de 3 %. Pour des altitudes de quelques kilomètres, la variation de g est négligeable.
Une autre conséquence de ladite rotation est que la Terre n’est pas une sphère parfaite et est aplatie aux pôles. Le rayon de la Terre au niveau de l’équateur et des pôles diffère de quelques dizaines de kilomètres.
Cela a pour effet que l’intensité de la pesanteur à la surface terrestre
|
|
Latitude | |
| Pôle Nord | 9,83 | 90° N |
| Paris | 9,81 | 49° N |
| Équateur | 9,78 | 0° |
Après, rappelons-nous que la matière crée la gravitation. Comme le globe n’est pas parfaitement lisse, l’intensité de la pesanteur présente de légères fluctuations selon le relief ou la géologie de la région étudiée.
D’autre part, il a été observé des variations du champ de pesanteur en fonction du temps, explicables par les mouvements de la matière dans les profondeurs de la Terre.
Ces deux types de fluctuations sont nommées anomalies du champ gravitationnel.
En un point P, à une distance r, ce champ s’écrit :
Un corps de masse m plongé dans ce champ subit une force d’attraction gravitationnelle
Le champ de gravitation terrestre
Sa norme
La force d’attraction gravitationnelle
Le champ de pesanteur est considéré localement comme uniforme, même s’il varie légèrement avec l’altitude ou la latitude du lieu de mesure.
Teste dès maintenant tes nouvelles connaissances dans notre quiz
Vous avez obtenu75%de bonnes réponses !
Reçois l’intégralité des bonnes réponses ainsi que les rappels de cours associés

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !








