Le modèle de Hardy-Weinberg et les causes de la déviation au sein des populations naturelles
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Comprendre et utiliser le modèle de Hardy-Weinberg.
- Déterminer lorsqu’un allèle est soumis à une force évolutive.
- Il est possible de calculer et de modéliser l’évolution de la diversité génétique d’une population grâce au modèle de Hardy-Weinberg.
- Ce modèle s’applique dans des conditions particulières.
- Lorsque ces conditions d’application sont respectées, les fréquences alléliques sont à l’équilibre et ne changent pas au cours des générations.
- Si une population n’est pas à l’équilibre de Hardy-Weinberg, c’est qu’elle est soumise à une force évolutive.
- L’apparition de nouveaux allèles dépend des modifications aléatoires de la séquence des gènes au moment de la réplication : les mutations.
- La sélection naturelle : les individus d’une même population n’ont pas tous le même avantage sélectif et le même succès reproducteur. Seuls ceux possédant ces deux critères pourront transmettre leur patrimoine génétique à la descendance.
- La sélection sexuelle repose sur le choix des partenaires reproductifs.
- La dérive génétique : chaque population est caractérisée par la fréquence de ses allèles. Dans des conditions où le milieu de vie est favorable, cette fréquence varie peu d’une génération à l’autre. Par contre, lorsque le nombre d’individus formant la population diminue de façon importante, certains allèles vont devenir prédominants et d’autres vont disparaitre.
- Ainsi, le hasard joue un rôle fondamental dans l’histoire évolutive d’une population : lors des modifications non prévisibles du milieu de vie, les individus ayant acquis des allèles leur conférant un avantage sélectif et présentant un avantage reproductif seront les plus à même de se reproduire, favorisant ainsi la transmission de leur patrimoine génétique à la descendance et modifiant la fréquence des allèles dans la population.
Le modèle de Hardy-Weinberg, du nom des deux scientifiques qui l’ont proposé au début du XXe siècle, est une formulation mathématique de la variation de la diversité génétique au sein des populations naturelles. Ce modèle a été une grande avancée pour la génétique et pour la compréhension de l’évolution des espèces. Ces travaux ont ensuite donné naissance à une nouvelle discipline, la génétique des populations.
Comme tout modèle, celui de Hardy-Weinberg est une simplification du monde réel, ce qui facilite la compréhension des processus naturels. Pour cela, il ne s’applique que dans des conditions d’applications particulières, celles qui définissent une population dite « idéale » :
- La population est de taille « infinie » (dans les faits on considère une population de grande taille comme infinie). Ceci empêche les effets de la dérive génétique.
- Il n’y a pas de mutation sur les allèles étudiés.
- La population est isolée des autres populations de la même espèce. Il n’y a aucun échange génétique avec une autre population.
- Les allèles étudiés n’apportent aucun avantage ou désavantage aux individus. Il n’y a pas d’influence due à la sélection naturelle.
- Il n’y a pas de sélection du partenaire, la reproduction entre les individus doit s’effectuer au hasard. Cette situation est nommée panmixie.
La panmixie est plus courante dans la nature que ce que l’on pourrait penser. C’est le cas des coraux qui libèrent leurs gamètes dans l’eau de mer, les fécondations s’effectuant au hasard des rencontres entre ovules et spermatozoïdes. C’est aussi le cas chez de nombreuses espèces végétales, dont le pollen est transporté par le vent ou les pollinisateurs.
Les conditions d’application du modèle sont chacune relatives à une force évolutive (sélection naturelle, dérive génétique, etc.). Si une population étudiée dans la nature ne présente pas la diversité génétique prévue par le modèle, on en conclut que cette population est soumise à l’influence d’une ou de plusieurs forces évolutives.
Prenons une population théorique. Pour un locus donné, cette population possède deux allèles A et a.
Les individus de cette population peuvent donc présenter trois génotypes pour ce locus :
- Ils peuvent être homozygotes (A//A).
- Ils peuvent être hétérozygotes (A//a).
- Ils peuvent être homozygotes (a//a).
Expérimentalement, les scientifiques ont accès aux génotypes par l’observation du phénotype des individus. Il est donc possible de réaliser des comptages d’individus selon leur génotype.
Les fréquences génotypiques au sein d’une population correspondent à la fréquence de chaque génotype dans celle-ci. Elle est exprimée par un chiffre compris entre 0 et 1.
Elle se calcule ainsi : ![]()
Dans la population présentée ci-dessus, on a compté 523 individus possédant le génotype (a//a) et le nombre total d’individus est 1235. La fréquence du génotype (a//a) est donc de
La somme de toutes les fréquences génotypiques au sein d’une population doit être égale à 1.
La seconde étape pour établir le modèle est le calcul des fréquences alléliques au sein de la population. Elles correspondent à la fréquence de chaque allèle au sein de la population. Elles sont calculées à partir des fréquences génotypiques. Lorsque deux allèles sont étudiés, les fréquences alléliques sont nommées p et q.
Fréquence allélique de
A : ![]()
Fréquence allélique de
a : ![]()
De plus : p + q = 1
Dans une population, les fréquences génotypiques sont (AA) = 0,35, (Aa) = 0,5 et (aa) = 0,15. On a
Prenons une population respectant les conditions d’application de Hardy-Weinberg. Pour un locus donné, cette population possède deux allèles, A et a, dont nous connaissons les fréquences alléliques p et q.
Par facilité, on suppose que tous les individus se
reproduisent simultanément et libèrent
leurs gamètes de façon
synchronisée.
Par définition, les gamètes ne
possèdent qu’un seul allèle pour le
locus considéré, c'est-à-dire
qu’un gamète possède soit A,
soit a. De plus, les fréquences
alléliques chez les gamètes sont les
mêmes que celles de la population
étudiée.
Ainsi, la fréquence des gamètes
possédant l’allèle A est
p et celle de gamètes possédant
l’allèle a est q.
Grâce à un tableau de croisement, il est possible de déterminer la proportion théorique de chaque croisement et d’en déduire les fréquences génotypiques de la génération suivante.
|
Gamètes maternels Gamètes paternels |
allèle A fréquence = p |
allèle a fréquence = q |
|
allèle A fréquence = p |
(A//A) fréquence = p² |
(A//a) fréquence = pq |
|
allèle a fréquence = q |
(A//a) fréquence = pq |
(a//a) fréquence =q² |
Les fréquences génotypiques de la génération suivante sont donc :
- Fréquence de (A//A) = p
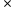 p = p²
p = p²
- Fréquence de (A//a) =
p
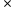 q
+ p
q
+ p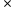 q = 2pq
q = 2pq
- Fréquence de (a//a) =
q
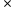 q
= q²
q
= q²
Pour finir la modélisation, nous pouvons déterminer les fréquences alléliques de la génération suivante à partir des fréquences génotypiques obtenues à partir du modèle.
On pose pn+1 la fréquence allélique de p à la génération suivante. Calculons la fréquence de A à la génération suivante :
![]()
![]()
On pose q = 1 – p
![]()
![]()
![]()
On en déduit ![]()
La fréquence allélique de A est la même la génération suivante, tout comme la fréquence de a. Ainsi, lorsque les conditions d’application sont réunies, les fréquences alléliques et génotypiques ne changent pas au fil des générations. C’est ce que l’on nomme l’équilibre de Hardy-Weinberg.
La conclusion de ce modèle est que seules les forces évolutives font varier les fréquences alléliques au sein des populations naturelles.
Les forces évolutives sont la sélection naturelle, la dérive génétique, la sélection sexuelle, les mutations et les échanges génétiques avec les autres populations.
Si pour un locus donné, les fréquences alléliques d’une population naturelle ne sont pas à l’équilibre, c’est qu’au moins une de ces forces est à l’œuvre.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !









