L'apport de la chronologie absolue dans la datation des évènements géologiques
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
- Comprendre le principe de la datation absolue.
- Utiliser les radiochronomètres pour dater une
roche :
- Dater avec le couple de radiochronomètres Rb/Sr.
- Dater avec le couple de radiochronomètres K/Ar.
- Les roches contiennent des isotopes radioactifs naturels qui sont instables et se désintègrent de manière continue et irréversible en isotopes stables, appelés isotopes fils.
- La désintégration d'un isotope
père suit une loi appelée loi de
désintégration
radioactive :
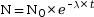où N0 représente la
quantité initiale d'isotope
père, λ la constante de
désintégration propre à l'isotope et
t le temps
depuis la fermeture du système.
- La désintégration des isotopes radioactifs naturels et l’apparition des éléments fils permet de dater la formation des roches. On utilise pour cela des radiochronomètres : des couples d'isotopes radioactifs.
- Avec le radiochronomètre Rb/Sr, on effectue
plusieurs mesures puis on représente le
rapport
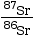en fonction du
rapport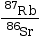 
. La pente a de la droite permet de
déterminer l’âge de la roche, selon la
formule :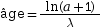 
, avec λ la constante de
désintégration du rubidium.
- Le potassium 40 se désintègre en
argon 40 et en calcium 40. Avec ce
radiochronomètre, il est possible de connaitre
l’âge de la roche en utilisant la formule
:
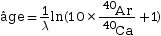où λ est la constante de
désintégration du potassium.
Pour réaliser une datation absolue, il est nécessaire d'utiliser des isotopes radioactifs présents dans les roches, et plus précisément dans les minéraux.
Il existe en effet des éléments chimiques possédant des isotopes naturels radioactifs. Lors de leur désintégration, ces éléments émettent des rayonnements et se transforment en éléments stables, présentant une légère différence de masse. Les roches de type magmatique et métamorphique sont de bons candidats pour la datation par radiochronologie. Elles contiennent naturellement des isotopes radioactifs dans un système fermé lors de la cristallisation des minéraux.
Pour comprendre la datation absolue, il est tout d'abord nécessaire de distinguer deux éléments : l'isotope père et l'isotope fils.
L'isotope père est un atome radioactif qui va se désintégrer de manière continue au cours du temps, en suivant une constante de désintégration. Cette constante de désintégration est spécifique de chaque isotope.
L'isotope fils se forme après la désintégration de l'isotope père. La quantité d’isope fils va augmenter dans le minéral, à mesure que la quantité d’isotope père diminue. Cet isotope fils, au contraire de l’isotope père, n'est pas radioactif, il est stable.
La spectrométrie de masse permet de doser la quantité des différents isotopes présents dans un échantillon.
La désintégration isotopique étant constante et mesurable, il est possible de mesurer le temps depuis la formation de la roche. Les isotopes permettent donc de dater la période de formation de la roche, ce sont des chronomètres.
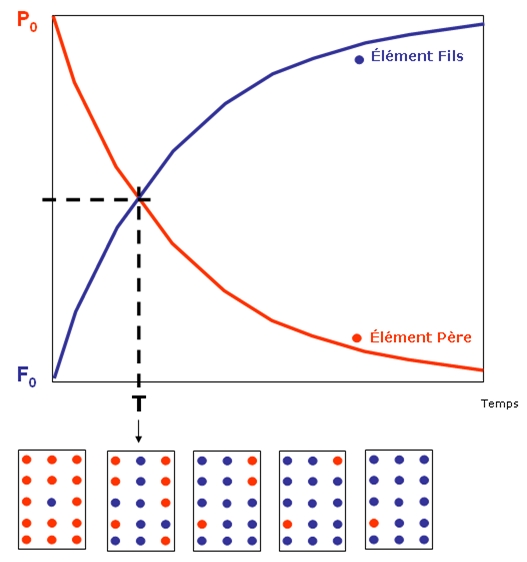
Chaque isotope radioactif possède une demi-vie ou période radioactive (T) qui correspond au temps nécessaire à la désintégration de la moitié de la population initiale (N0) d’isotope radioactif.
Elle se calcule à l’aide de la formule suivante :
|
Avec :
|
Le tableau suivant donne la constante de désintégration et la demi-vie des isotopes les plus utilisés.
| Noyau père | Noyau fils | Constante radioactive (λ) | Demi-vie (T) |
| 14C | 14N | 1,209·10-4 a-1 | 5 730 a |
| 40K | 40Ar | 5,81·10-11 a-1 | 11,9 Ga |
| 40K | 40Ca | 4,962·10-10 a-1 | 1,40 Ga |
| 87Rb | 87Sr | 1,42·10-11 a-1 | 48,8 Ga |
| 138La | 138Ce | 2,67·10-12 a-1 | 259,6 Ga |
| 147Sm | 143Nd | 6,54· 10-12 a-1 | 106 Ga |
| 176Lu | 176Hf | 1,94· 10-11 a-1 | 35,7 Ga |
| 187Re | 187Os | 1,64· 10-11 a-1 | 42,3 Ga |
| 232Th | 208Pb | 4,9475· 10-11 a-1 | 14,0 Ga |
| 235U | 207Pb | 9,8485·10-10 a-1 | 0,704 Ga |
| 238U | 208Pb | 1,55125· 10-10 a-1 | 4,47 Ga |
Pour calculer les quantités d’isotopes dans les minéraux, il est nécessaire d'utiliser un spectromètre de masse.
De manière générale, la désintégration de l'isotope radioactif (l’isotope père) suit une loi de décroissance exponentielle :
|
Avec :
|
À partir de la formule initiale, nous pouvons
obtenir : 
Cette formule permet de calculer le temps
écoulé depuis le moment où le
système s’est fermé, et donc de
déterminer la date qui correspond à ce
moment. Cette date correspond soit à la mort de
l'animal, soit à la cristallisation du magma.
Un problème pouvant être rencontré avec cette datation est l’ouverture du système, c'est-à-dire la modification par l’environnement des quantités d’isotope père et d’isotope fils, comme lors d’une recristallisation. Dans ce cas précis, la datation permettra de mesurer le moment de la recristallisation.
Le rubidium 87 se désintègre en strontium 87 (87Sr) selon une période radioactive de 50 × 109 années.
Les roches contiennent aussi du 86Sr qui est un élément stable. Sa quantité ne varie donc pas dans un système fermé.
Au temps t = 0, correspondant à la date de cristallisation du magma, les échantillons de roches ont tous du 87Rb et du 86Sr. Par contre, il n’y a pas de 87Sr.
Au cours du temps, la quantité de 87Rb diminue au profit du 87Sr.
Afin de déterminer l’âge d’une roche, on quantifie ces éléments dans différents minéraux constituant la roche. Pour la datation avec le couple rubidium/strontium, nous utilisons la formule suivante :
|
Avec :
|
Nous ne connaissons pas N0, la quantité initiale de l'élément radioactif (l’isotope père). Il est donc nécessaire de modifier l’équation et d’utiliser la quantité d’isotopes fils. L’équation obtenue est la suivante :
|
Avec :
|
Dans notre cas, l’élément fils est le strontium 87, et il y en avait initialement, mais nous ne connaissions pas sa quantité. L’équation devient :
Nous savons que le rapport isotopique 
reste une constante dans tous les
minéraux d’une même roche. De plus, le
strontium 86 n’étant pas radioactif, sa
quantité ne variera pas au cours du temps.
L’équation finale devient donc :
On trace donc la courbe représentant le
rapport en fonction du
rapport .
Les points des minéraux d’une même roche se retrouvent alignés sur une droite de formule y= ax+b.
Avec : 
et 
La pente a de la courbe permet de
déterminer l’âge de la roche selon la
formule :
Avec : 
.
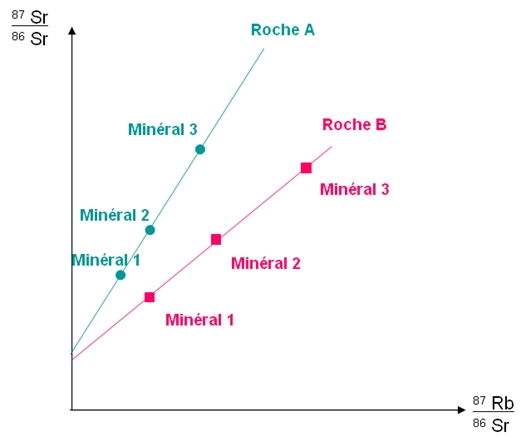
La radiochronologie permet ainsi de déterminer l’âge des roches. Associée à l’étude pétrographique, elle permet de reconstituer l’histoire géologique d’une région.
Le potassium 40, qui est radioactif, est présent dans les roches et se désintègre en argon 40 et en calcium 40. Chacune de ces désintégrations dispose de sa propre constante de désintégration. La constante de désintégration totale est égale à 5,543·10-10 an-1, car la constante pour la désintégration en calcium est de 4,96 ·10-10 an-1, et celle pour la désintégration en argon est de 5,8·10-11 an-1.
Les calculs permettent de montrer que 
et que cette valeur est une constante.
Il est de ce fait possible de connaitre
l’âge de la roche en utilisant la formule
suivante :
La méthode potassium/argon est surtout utilisée pour dater des roches volcaniques car, pour les autres roches, plusieurs paramètres peuvent fausser les résultats.
Pour que la méthode soit valide, le premier point à vérifier est l'absence d'argon dans la roche.
De fait, l’argon est un gaz qui va souvent disparaitre lors de la fermeture du système, car les roches volcaniques, lors de leur cristallisation, vont dégazer. Ce paramètre est donc le plus souvent validé pour les roches volcaniques.
Le second point à vérifier est que les mesures sont réalisées dans un système clos. Il ne doit pas y avoir de contamination par l'argon.
De plus, cette technique utilise deux appareils différents de mesure, chacun d’eux ayant ses propres erreurs de mesure. Il est donc nécessaire d'être attentif sur les résultats obtenus avec cette datation.
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fiches de cours les plus recherchées
SVT
Utilisation des cartes géologiques pour mettre en évidence des orogenèses
SVT
La recherche d'un océan disparu à l'aide de la carte de France au millionième
SVT
Mise en évidence du fonctionnement des marges passives
SVT
Les étapes de la photosynthèse
SVT
Le devenir des produits de la photosynthèse
SVT
Mise en évidence des variations récentes du climat : l'alternance climatique du quaternaire
SVT
Les effets du réchauffement climatique sur la biodiversité
SVT
Rôle de la plasticité cérébrale dans l'apprentissage et la récupération
SVT
Le stress aigu : acteurs et mécanismes
SVT
Le stress chronique : conséquences et moyens de lutte
Fermer
Accédez gratuitement à
