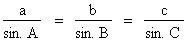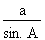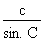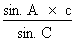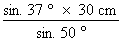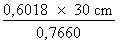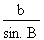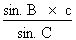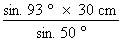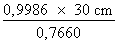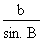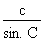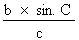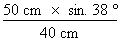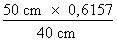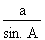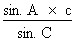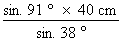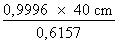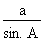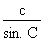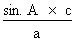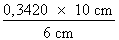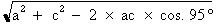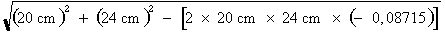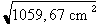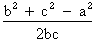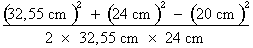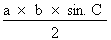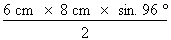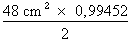Trigonométrie appliquée aux triangles quelconques
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
 Trigonométrie
appliquée aux triangles quelconques
Trigonométrie
appliquée aux triangles quelconques
En mécanique industrielle, il n'est pas toujours possible de résoudre des problèmes de trigonométrie à l'aide de triangles rectangles.
Les problèmes rencontrés impliquent parfois des triangles quelconques.
Dans cette étude, vous verrez comment résoudre ce type de problèmes.
Vous venez de voir que, pour résoudre des problèmes concernant des triangles rectangles, il faut recourir aux fonctions trigonométriques de base.
Les calculs se rapportant aux triangles quelconques s'effectuent à l'aide de deux lois :
- la loi des sinus ;
- la loi des cosinus.
Loi des sinus
|
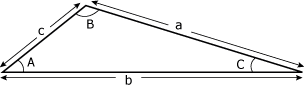
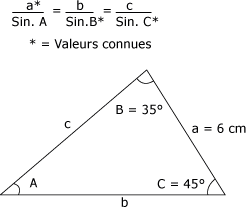
La loi des sinus établit que le rapport entre la mesure du côté opposé à un angle et le sinus de cet angle est équivalent pour tous les angles d'un triangle quelconque (figure 4.32). |
Figure 4.32 Loi des sinus.
|
Si l'on se reporte au triangle de la figure 4.32, on peut énoncer la loi des sinus comme suit : |
La loi des sinus s'applique dans deux cas particuliers :
- lorsque l'on connaît la valeur de deux angles et un côté d'un triangle quelconque ;
- lorsque l'on connaît la valeur de deux côtés d'un triangle et de l'angle opposé à l'un deux.
Loi des sinus: application 1
L'exemple suivant montre comment appliquer la loi des sinus.
|
Problème 1:
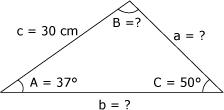
A partir du triangle de la figure 4.33, trouvez : a) la valeur du côté a ; b) la valeur de l'angle B ; c) la valeur du côté b. Figure 4.33 Triangle 16.
1. Identification des données Nous connaissons la valeur de deux angles et d'un côté du triangle :
Il s'agit donc du premier cas d'application de la loi des sinus. 2. Calcul de la valeur du côté a La loi des sinus nous permet d'établir la relation suivante :
Isolons le côté a :
a =
a =
a = a = 23,569 cm 3. Calcul de la valeur de l'angle B Comme nous connaissons la valeur de deux des angles du triangle, il est possible de trouver la valeur du troisième : angle B = 180° - (angle C + angle A) angle B = 180° - (50° + 37°) angle B = 93 ° 4. Calcul de la valeur du côté b De la loi des sinus, nous tirons la relation suivante :
Isolons le côté b :
b =
b =
b = b = 39,11 cm Nous avons calculé toutes les valeurs manquantes du triangle de la figure 4.33 : - côté a = 23,569 cm - angle B = 93° - côté b = 39,11 cm |
Loi des sinus: application 2
L' exemple suivant montre comment appliquer la loi des sinus.
|
Problème 2:
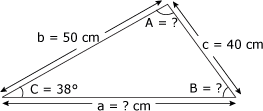
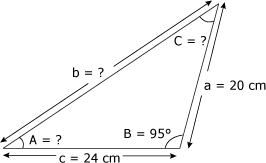
A partir du triangle de la figure 4.34, trouvez la valeur : a) de l'angle B ; b) de l'angle A ; c) du côté a. Figure 4.34 Triangle 17.
1. Identification des données Il s'agit ici du deuxième cas d'application de la loi des sinus. En effet, nous connaissons la valeur de deux côtés du triangle et celle de l'angle opposé à l'un deux :
2. Calcul de la valeur de l'angle B La loi des sinus nous permet d'établir la relation suivante :
Isolons le sinus de l'angle B :
sin. B =
sin. B =
sin. B = sin. B = 0,76962 Trouvons maintenant la valeur de l'angle B en degrés-minutes-secondes à l'aide de la calculatrice : 0,76962 inv sin. = 50,3159° 50,3159 inv DMS = 50° 19' 11" 3. Calcul de la valeur de l'angle A Puisque nous connaissons maintenant la valeur de deux des angles du triangle, il devient facile de déterminer la valeur du troisième angle : angle A = 180° - (angle B + angle C) angle A = 180° - (50,32° + 38°) angle A = 91,68°
Convertissons la réponse en degrés-minutes-secondes : 91,68 inv DMS = 91° 41' L'angle A vaut 91° 41'. 4. Calcul de la valeur du côté a La loi des sinus nous permet de poser la relation suivante :
Isolons le côté a :
a =
a =
a = a = 64,94 Nous avons donc déterminé la valeur des mesures manquantes du triangle de la figure 4.34 : angle B = 50° 19' angle A = 91° 41' côté a = 64,94 cm
|
Angles obtus
Il faut porter une attention particulière aux triangles quelconques possédant un angle obtus (plus de 90°).
Lorsque l'on cherche à déterminer la valeur d'un angle obtus à l'aide de la valeur décimale de son sinus, la calculatrice affiche la valeur du plus petit angle correspondant à ce sinus, c'est-à-dire l'angle supplémentaires de l'angle obtus.
|
Pour trouver la valeur réelle d'un angle obtus, on doit donc soustraire de 180° la valeur de son angle supplémentaire. |
L'exemple suivant illustre ce principe.
|
Problème
La valeur naturelle du sinus de l'angle C du triangle de la figure 4.35 égale 0,7071. Quelle est la valeur de cet angle obtus ? Figure 4.35 Triangle 18.
1. Identification des données La figure 4.35 nous permet d'établir que :
2. Calcul du sinus de l'angle C Appliquons la relation établie par la loi des sinus :
Isolons le sinus de l'angle C :
sin. C =
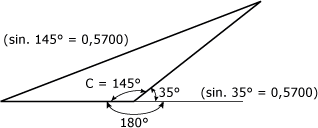
sin. C = sin. C = 0,5700 3. Calcul de la valeur de l'angle C Trouvons à quel angle correspond le sinus 0,5700 à l'aide de la calculatrice : 0,5700 inv sin. = 34,75° Arrondissons le résultat à 35°. Si l'on observe la figure 4.35, il devient évident que l'angle C est beaucoup plus grand que 35° :
Pour obtenir la valeur réelle de l'angle C, nous devons donc trouver la valeur de l'angle supplémentaire de l'angle de 35° : angle C = 180° - 35° angle C = 145° L'angle C mesure 145°, comme le montre la figure 4.36. Figure 4.36 Valeur de l'angle C.
|
Loi des cosinus
La loi des cosinus s'applique lorsque l'on connaît une valeur dans chaque rapport composant la loi des sinus.
Prenons par exemple, le triangle de la figure 4.39.
Il est possible d'y appliquer la loi des cosinus pour trouver les dimensions manquantes, puisque l'on connaît une valeur de chaque terme de la loi des sinus.
Figure 4.39 Loi des cosinus.
Si l'on utilise la figure 4.39 comme référence, on peut énoncer la loi des cosinus de la manière suivante :
c2 = a2 + b2 - 2ab cos. C
- a2 est equivalent à a au carré
- b2 est equivalent à b au carré
- c2 est equivalent à c au carré
Cette relation est valable pour tous les côtés d'un triangle quelconque, d'où :
- b2 = a2 + c2 - 2ac cos. B
- a2 = b2 + c2 - 2bc cos. A
A partir de l'énoncé de la loi des cosinus, on peut tirer les équations suivantes :
cos. A =
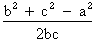
cos. B =
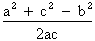
cos. C =
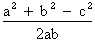
Loi des cosinus: application
L'exemple qui suit vous permettra de vous familiariser avec la loi des cosinus.
|
Problème
A partir de la figure 4.40, calculez :
Figure 4.40 Triangle 21.
1. Identification des données La figure 4.40 indique que le côté a du triangle mesure 20 cm, le côté c, 24 cm et que l'angle B mesure 95°. 2. Calcul de la valeur du côté b La loi des cosinus nous permet de poser l'équation suivante :
Comme vous venez de le constater, le cosinus de l'angle de 95° possède une valeur négative. C'est le cas du cosinus de tous les angles obtus. Les angles supplémentaires ont le même cosinus, mais celui-ci est positif. Par exemple, le cosinus de 85° (angle supplémentaire de 95°) est de 0,08715. 3. Calcul de la valeur de l'angle A Appliquons l'équation suivante, découlant de la loi des cosinus :
A l'aide de la calculatrice, nous pouvons déterminer que le cosinus 0,79077 correspond à un angle de 37° 44 ‘ : angle A = 37° 44' 4. Calcul de la valeur de l'angle C Calculons la valeur de l'angle C à partir de la valeur des angles A et B :
La loi des cosinus nous a donc permis de trouver les valeurs manquantes du triangle de la figure 4.40 :
|
Aire des triangles
La trigonométrie permet aussi de trouver l'aire des triangles.
| l'aire d'un triangle est égale à la moitié du produit de deux côtés quelconques et de la valeur naturelle du sinus de l'angle inclus. |
Voyons, à l'aide d'un exemple, comment s'applique ce principe.
|
Problème
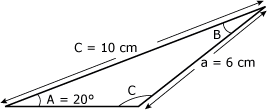
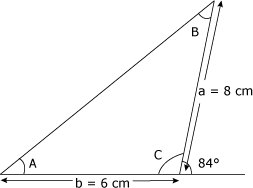
Calculez l'aire du triangle de la figure 4.43. Figure 4.43 Triangle 24.
1. Identification des données Pour pouvoir calculer l'aire du triangle, il nous faut connaître la valeur de l'angle inclus entre les côtés a et b. 2. Calcul de la valeur de l'angle inclus L'angle C est égal à :
3. Calcul de l'aire Il ne nous reste plus qu'à appliquer la formule de calcul de l'aire :
Atriangle =
Atriangle =
Atriangle = Atriangle = 23,87 cm2 ainsi L'aire du triangle mesure 23,87 cm2.
|

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !