Séquenceur pneumatique
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Cette étude vous présente le séquenceur pneumatique comme moyen de réalisation des automatismes séquentiels.
Elle est composée :
- d'une description du principe de fonctionnement du séquenceur pneumatique,
- d'une application dans la réalisation pratique d'un automatisme dont le Grafcet est à séquence unique.
Description du séquenceur pneumatique :
Le séquenceur pneumatique est une association linéaire de modules d'étape.
Un module d'étape correspond à une étape du Grafcet et son fonctionnement traduit les règles d'évolution du Grafcet.
Une mémoire pneumatique bistable est l'élément logique de base de la réalisation d'un module d'étape.
Principe de base du fonctionnement d'un module d'étape :
Le module d'étape est construit à partir d'une mémoire bistable et de portes logiques pour respecter les règles d'évolution du Grafcet. Pour que le fonctionnement du module d'étape soit conforme aux règles d'évolution d'une étape du Grafcet, il faut tenir compte des conditions suivantes lors de sa réalisation :
- L'action associée à une étape a lieu si l'étape est active.
- Une étape est considérée activée si l'étape précédente est active et que la réceptivité associée à la transition est logiquement "VRAIE".
- Une étape doit être désactivée si l'étape suivante est active.
Une mémoire pneumatique bistable dispose de deux signaux d'entrée (signal de mise à 1 et signal de mise à 0) et de deux sorties complémentaires.
L'activation de la mémoire se fait quand le signal de mise à 1 est à l'état logique 1 alors que sa désactivation est possible quand le signal de mise à 0 est à l'état logique 1.
Ainsi, les conditions de fonctionnement du module d'étape qu'il faut respecter peuvent se traduire de la façon suivante :
- La mémoire délivrera un signal de sortie si elle est activée. Ce signal servira à commander l'action.
- Le signal de mise à 1 de la mémoire sera constitué par la multiplication logique du signal de l'étape précédente et la réceptivité associée à la transition précédente. De cette manière, l'activation de la mémoire se fera à la seule condition que l'étape précédente soit active et que la réceptivité associée à la transition précédente soit logiquement "VRAIE" conformément aux règles d'évolution du Grafcet.
- La mémoire doit être désactivée lorsque la mémoire suivante devient active. Ceci peut être réalisé en connectant la sortie de la mémoire suivante au signal de mise à 0 de la mémoire. De cette manière, la mémoire est désactivée quand la mémoire suivante est activée.
La figure suivante présente la description schématique de la réalisation d'un module d'étape.
Description schématique de la réalisation d'un module d'étape :
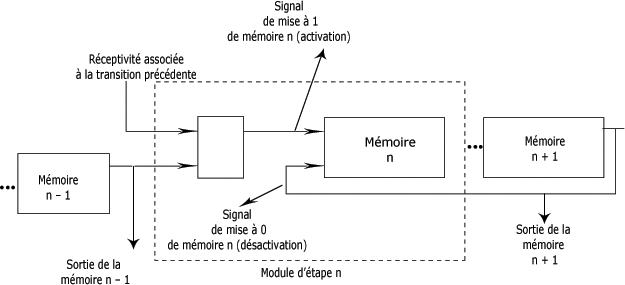
Sur cette figure, vous remarquez que la mémoire "n - 1" représente l'étape précédente alors que la mémoire "n + 1" désigne l'étape suivante de l'étape "n".
L'activation de la mémoire du module d'étape "n" ne sera possible que lorsque le signal à la sortie de la mémoire "n - 1" est à l'état logique 1 et que la réceptivité de la transition entre l'étape "n - 1" et l'étape "n" est logiquement "VRAIE".
C'est une cellule logique "ET" qui réalise cette condition logique. Cette cellule admet donc comme entrée, la sortie de la mémoire "n - 1" et un signal de capteur qui indique si la réceptivité associée à la transition entre l'étape "n - 1" et "n" est logiquement "VRAIE".
La sortie de cette cellule logique "ET" constitue le signal de mise à 1 de la mémoire "n". Le signal de mise à 0 de cette mémoire est constitué par la sortie de la mémoire "n + 1". Ainsi, quand la sortie de la mémoire "n + 1" sera active, la mémoire "n" doit être désactivée conformément aux règles d'évolution du Grafcet.
Les modules d'étape commerciaux peuvent présenter certaines propriétés particulières selon leur fabricant. Par exemple, le module d'étape de Parker permet une remise à 0 générale (RAZ). Cette remise à 0 générale est assurée par un signal qui agit sur les entrées de mise à 0 de chacune des mémoires des modules d'étape.
Dans ce module d'étape, une cellule logique "OU" est ajoutée au schéma du principe de base. Cette cellule admet comme entrées le signal de remise à 0 général (RAZ) et la sortie de la mémoire suivante. De cette façon, la mémoire présente peut être désactivée quand la mémoire suivante est activée ou quand le signal de remise à 0 général (RAZ) est à l'état logique 1. Le schéma de ce module d'étape est donné à la figure suivante.
Schéma de réalisation du module d'étape de Parker :
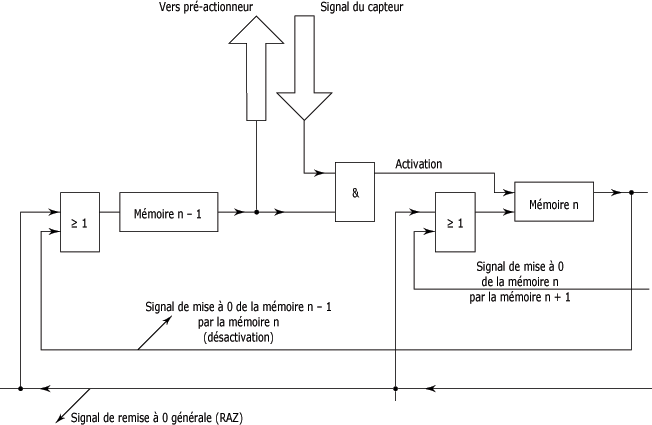
Certains modules d'étape présentent aussi des voyants lumineux qui identifient l'étape active à tout moment de l'évolution du Grafcet.
La réalisation pratique d'un séquenceur pneumatique est possible par la mise en cascade de plusieurs modules d'étape. On réalise ainsi une chaîne de modules d'étape.
Chaque module d'étape représente une étape du Grafcet à réaliser.
Ainsi, pour la réalisation d'un Grafcet à quatre étapes, on aura besoin d'un séquenceur à quatre modules d'étape. Les modules d'étape sont montés sur des plaques d'embase alors que deux plaques d'extrémité doivent être placées au début de la chaîne et à sa fin.
La plaque d'extrémité du début de la chaîne sert généralement à alimenter la chaîne en pression commune et à diriger le signal du début du cycle vers le premier module d'étape.
La plaque de la fin de la chaîne capte le signal de la fin du cycle et le retourne vers le signal de début du cycle.
Les fabricants de séquenceurs pneumatiques ont mis en place un standard de symbolisation logique des séquenceurs. Les séquenceurs commerciaux présentent des particularités différentes selon le fabricant. La figure suivante montre le schéma logique et le schéma d'usage d'un séquenceur Climax (système Polylog) sans remise à zéro générale à quatre modules d'étape.
Schéma logique et schéma d'usage d'un séquenceur Climax (système Polylog) à quatre modules d'étape :
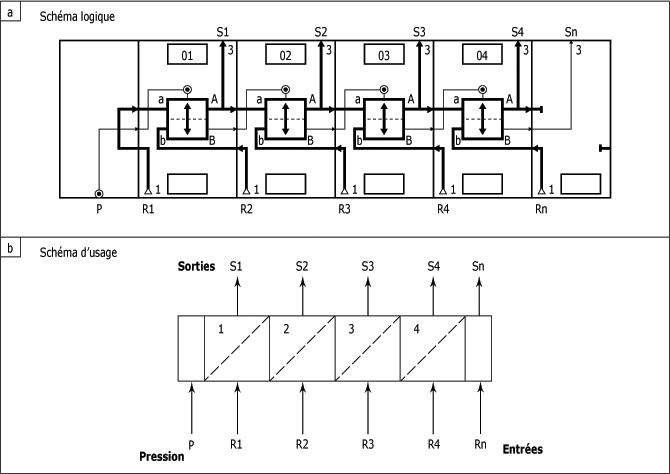
L'entrée désignée par la lettre P sur le symbole logique de ce séquenceur sert à alimenter les modules d'étape en air comprimé.
Ce séquenceur est composé de quatre modules d'étape identifiés par les chiffres 1, 2, 3 et 4. La sortie de chaque mémoire d'un module d'étape est désignée par la lettre S suivie du chiffre du module d'étape. Ainsi, la sortie S1 indique la sortie de la mémoire du module d'étape 1.
Les entrées identifiées par les lettres R indiquent les signaux d'activation de chaque module d'étape. Par exemple, l'entrée R1 sert à activer le module d'étape 1 et l'entrée R2 sert à activer le module d'étape 2.
L'entrée Rn désigne le signal de fin du cycle, elle met sous pression la sortie Sn qui, à son tour, peut commander le début d'un nouveau cycle du Grafcet.
Ce séquenceur à quatre modules d'étape peut ainsi servir à la réalisation d'une séquence à quatre étapes.
Schéma logique et schéma d'usage d'un séquenceur à trois modules d'étape :
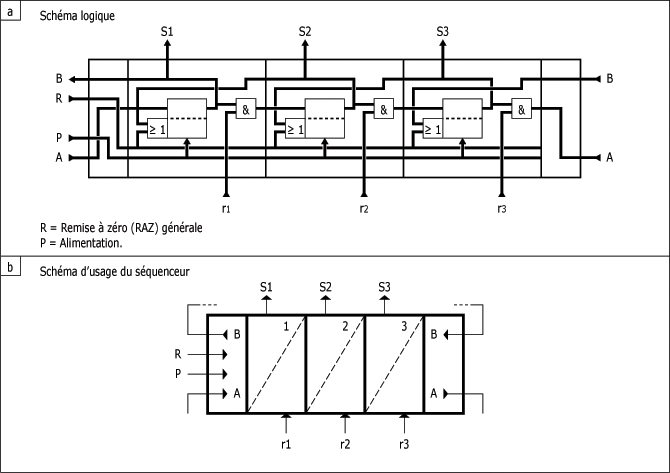
La figure ci-dessus vous présente un séquenceur à trois modules d'étape (Parker) avec remise à zéro (RAZ) générale, par le signal d'alimentation de l'orifice R.
Les figures suivantes vous présentent deux applications du séquenceur :
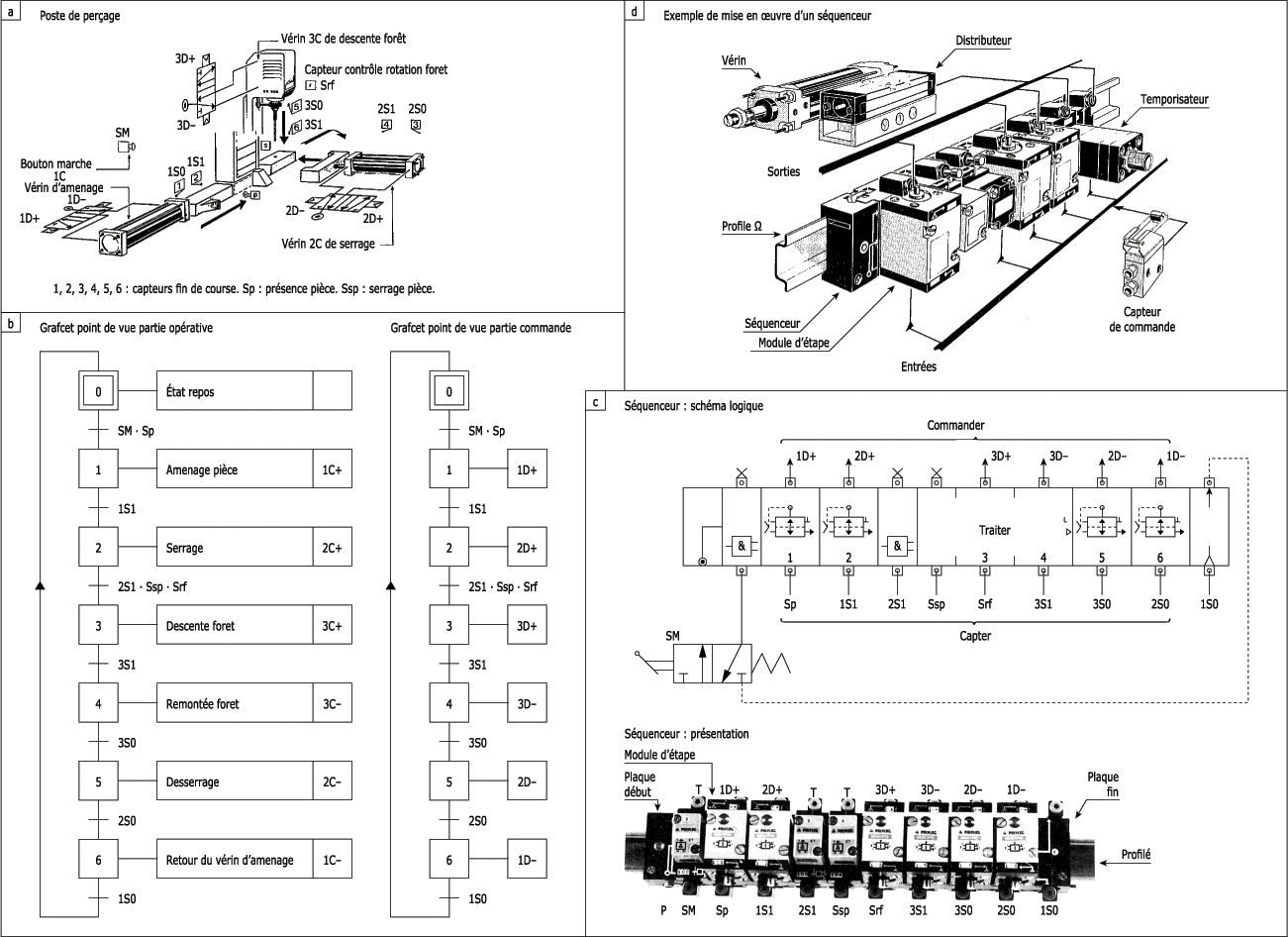
- Poste de perçage avec traitement de l'information par séquenceur Climax (système Polylog), figure suivante.
Poste de perçage - Séquenceur Climax (système Polylog) :
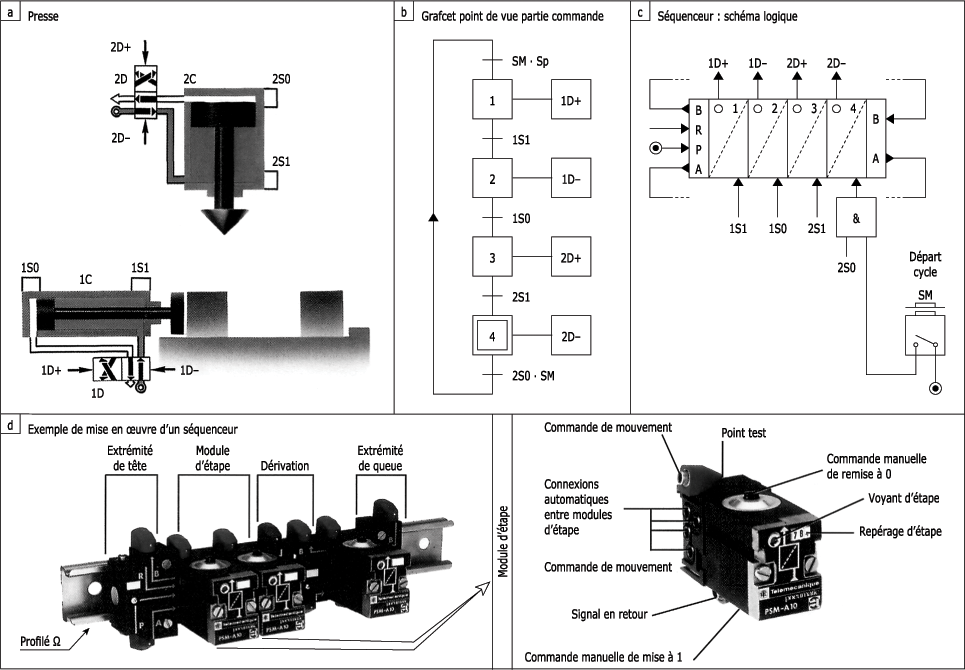
- Presse avec traitement de l'information par séquenceur Parker, figure suivante.
Presse - Séquenceur Parker :
Le séquenceur pneumatique est l'élément idéal pour la réalisation pratique des Grafcet à séquence unique. Le séquenceur est un ensemble modulaire, facile à installer et il permet de visualiser l'évolution des étapes actives du Grafcet.
A partir de l'exemple d'un Grafcet à séquence unique, vous allez comprendre le schéma de branchement nécessaire à la réalisation de l'automatisme.
Description de l'automatisme étudié : cycle carré
Considérez le Grafcet des mouvements (c'est une autre représentation du Grafcet point de vue partie opérative) que montre la figure suivante.
Grafcet des mouvements à séquence unique :
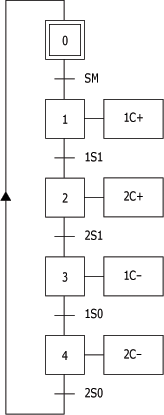
Il s'agit d'un automatisme qui commande deux vérins 1C et 2C. Les mouvements réalisés par l'automatisme sont les suivants :
- La sortie de la tige du vérin 1C. Cette sortie est identifiée par l'action 1C+ associée à l'étape 1.
- La sortie de la tige du vérin 2C. Cette sortie est identifiée par l'action 2C+ associée à l'étape 2.
- La rentrée de la tige du vérin 1C. Cette rentrée est identifiée par l'action 1C- associée à l'étape 3.
- La rentrée de la tige du vérin 2C. Cette rentrée est identifiée par l'action 2C- associée à l'étape 4.
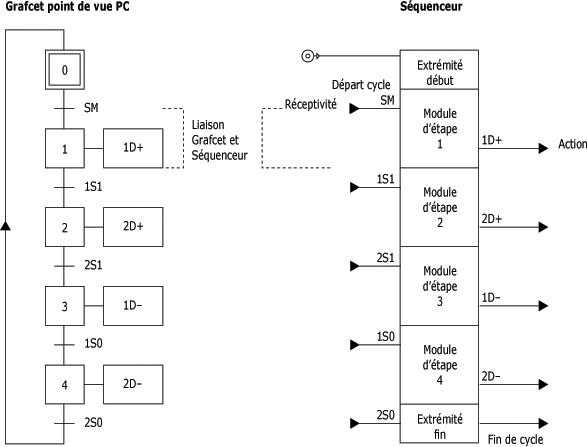
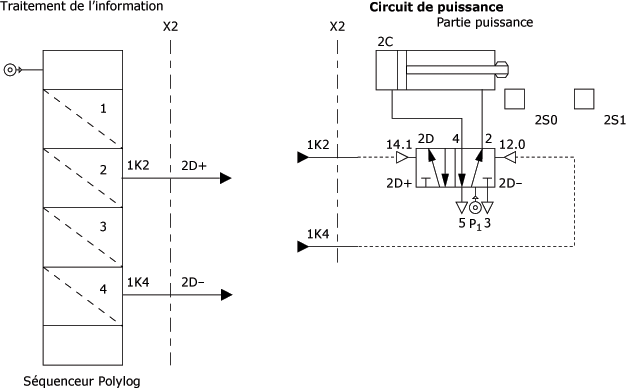
La figure suivante présente un Grafcet, point de vue PC et un séquenceur pneumatique. L'information SM (réceptivité) valide la transition qui active l'étape 1. Le séquenceur par sa disposition matérielle, exemple le signal SM et la sortie 1D+ (module d'étape 1), permet de visualiser le cycle du système.
Liaison Grafcet et séquenceur pneumatique :
Le cycle réalisé par cet automatisme est appelé cycle en "carré" parce que les mouvements effectués par les tiges des deux vérins 1C et 2C peuvent-être schématisés par un carré comme le présente la figure suivante.
Schéma du cycle en "carré" :
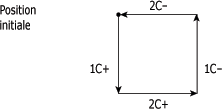
Les spécifications technologiques précisent la structure de l'automatisme.
La partie opérative qui se compose :
• De deux actionneurs :
- un vérin à double effet 1C (mouvement 1C+ et 1C-) ;
- un vérin à double effet 2C (mouvement 2C+ et 2C-) ;
• De capteurs 3/2 NF à commande par galet :
- Pour le vérin 1C, les références sont :
- 1S0 : actionné, position initiale, la tige du vérin est rentrée ;
- 1S1 : actionné, informe si la tige du vérin est sortie ;
- Pour le vérin 2C, nous aurons :
- 2S0 : actionné, position initiale, la tige du vérin est rentrée ;
- 2S1 : délivre un signal logique à l'état 1 si la tige du vérin est sortie.
La partie commande constituée par :
• Un séquenceur pneumatique, Polylog, composé de quatre modules d'étape :
- De deux pré-actionneurs :
- pour le vérin 1C l'énergie pneumatique est délivrée par le distributeur 5/2 bistable 1D, les orifices de pilotage sont désignés par 1D+ et 1D-.
- pour le vérin 2C, le distributeur associé 2D, reçoit les informations de commande par les orifices 2D+ et 2D-.
Le dialogue entre la partie commande et l'opérateur transite par un bouton-poussoir 3/2 NF à rappel par ressort, SM, réalisant la condition de réceptivité Marche. Le Grafcet point de vue partie commande présente le cycle, figure suivante.
Grafcet point de vue partie commande du cycle en "carré" :
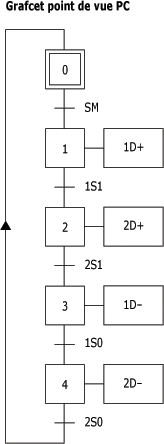
- A l'étape initiale, étape 0, l'automatisme est en attente d'un signal de départ du cycle. Aucune action n'est associée à cette étape.
- Le signal de départ du cycle SM sert à assurer le franchissement de la transition de l'étape 0 à l'étape 1. Ce franchissement doit donc activer l'étape 1. En pratique, on se servira de ce signal pour activer le module d'étape 1K1.
- Lorsque l'étape 1 est active, l'action est sortir la tige du vérin 1C. La sortie de la tige du vérin 1C est détectée par un capteur de fin de course qui donne le signal 1S1.
Ce signal permet de franchir la transition de l'étape 1 à l'étape 2. Dans la pratique, ceci se traduit par l'activation du module d'étape 1K2.
- L'action sortir la tige du vérin 2C est associée à l'étape 2. Cette action est détectée par un capteur de fin de course qui émet le signal 2S1. Ce signal sert à activer le module d'étape 1K3.
- A l'étape 3, la tige du vérin 1C doit être rentrée. La rentrée de cette tige est détectée par un capteur de fin de course qui donne le signal 1S0. Ce signal 1S0 servira à activer le module d'étape 1K4.
- La dernière étape de cet automatisme est l'étape 4. La tige du vérin 2C doit être rentrée lorsque cette étape est active. La rentrée de la tige du vérin 2C est détectée par un capteur de fin de course qui émet un signal 2S0.
Avec cette description du cycle de l'automatisme, des composants de la partie commande et de la partie opérative, vous allez réaliser différents câblages associés aux séquences.
Les schémas proposés permettent une réalisation progressive de l'ensemble de l'automatisme.
La figure suivante présente le schéma de branchement des signaux "entrées" du séquenceur ainsi que le circuit "Départ du cycle".
Schéma des branchements "entrées" du séquenceur et "Départ du cycle" :
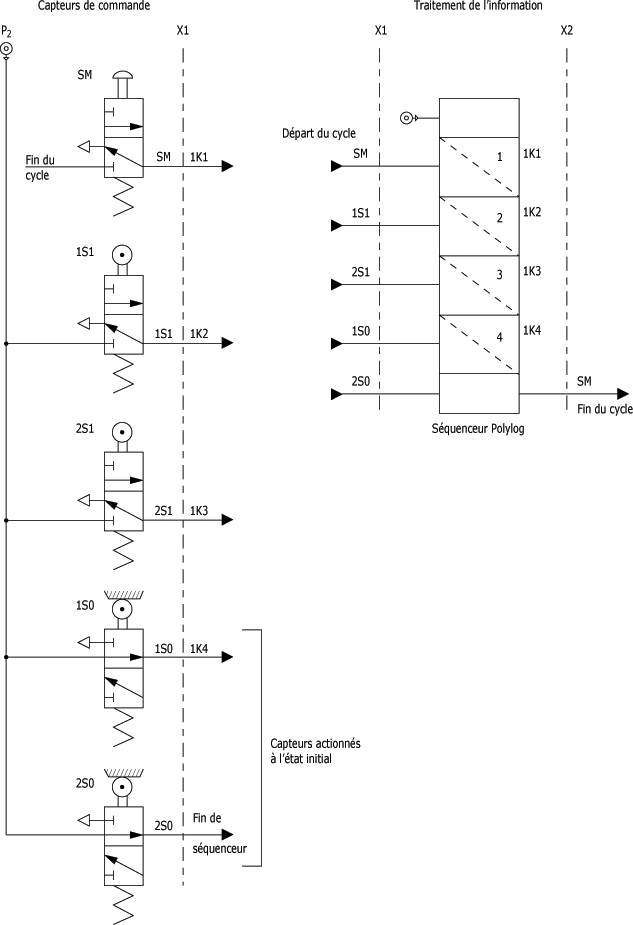
La figure ci-dessous et la figure ci-après vous présentent les branchements entre les sorties du séquenceur et la commande des pré-actionneurs 1D et 2D qui alimentent respectivement les vérins 1C et 2C.
Schéma des branchements "sorties" séquenceur et pré-actionneur du vérin 1C :
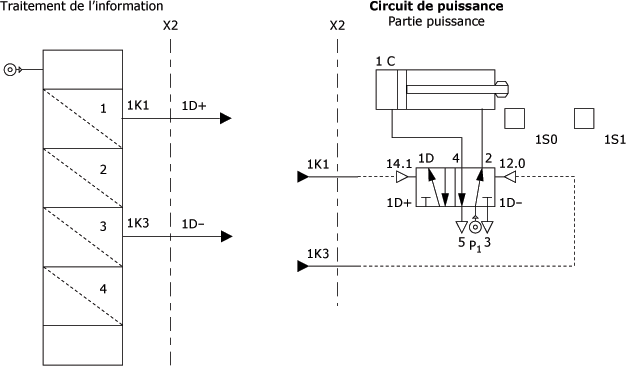
Schéma des branchements "sorties" séquenceur et pré-actionneur du vérin 2C :
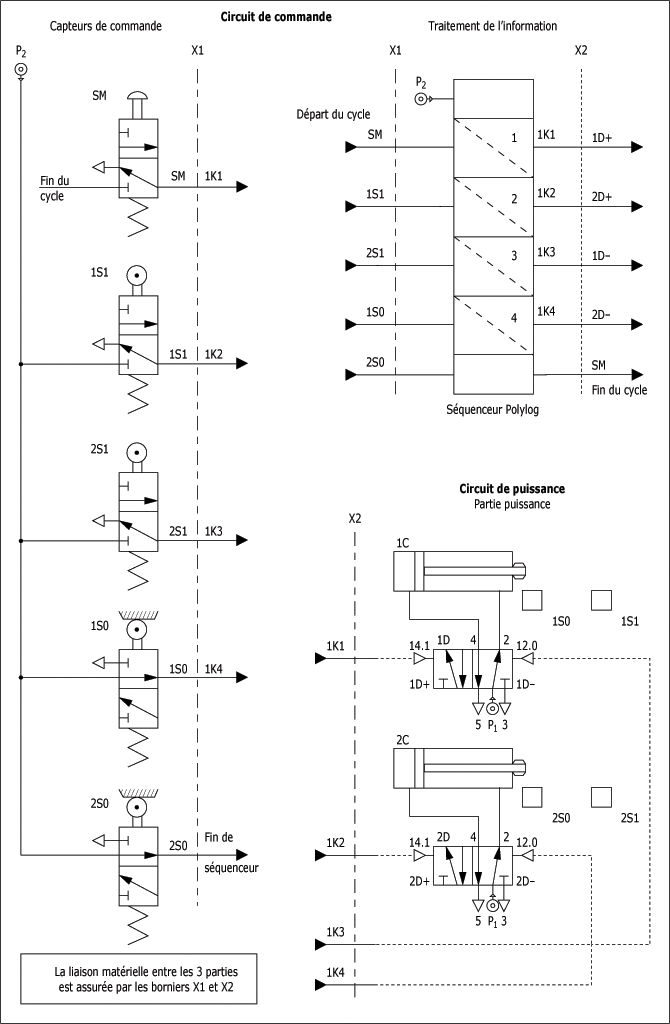
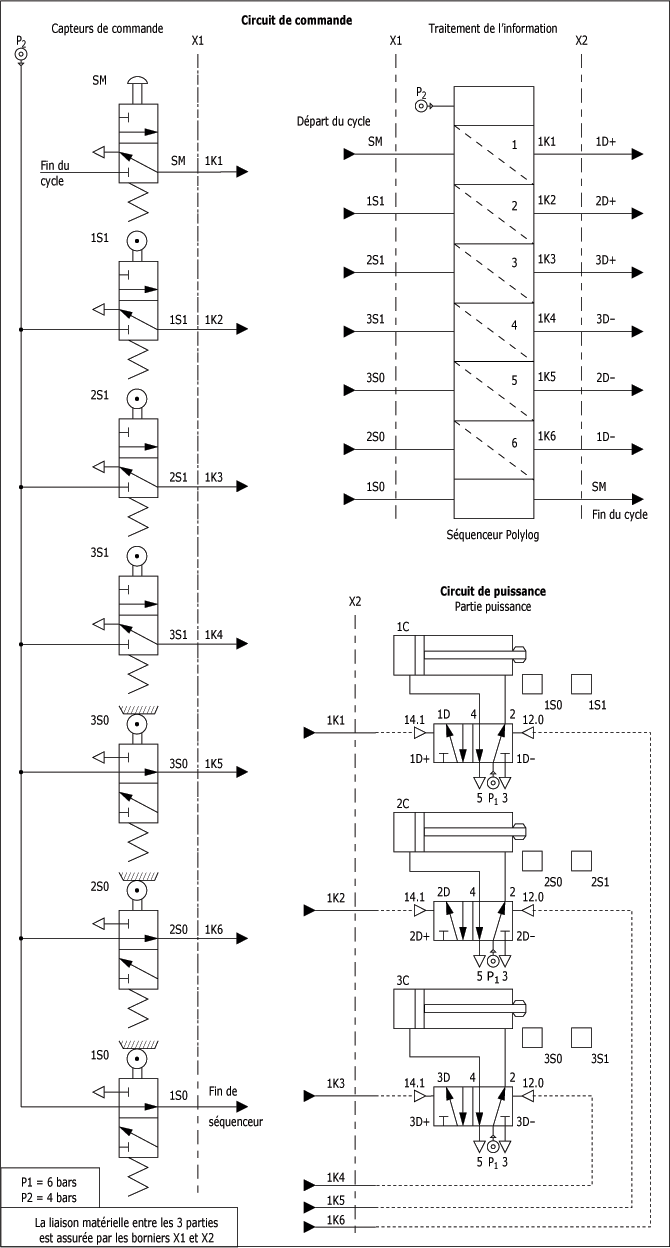
Le schéma de l'automatisme cycle en "carré" vous est présenté par la figure suivante. Les références X1 et X2 représentent des borniers qui assurent la liaison matérielle entre les représentations capteurs de commande, traitement de l'information et circuit de puissance.
Dans le cas d'un câblage définitif pour un système il sera nécessaire de repérer chaque borne de façon à assurer, dans les meilleurs délais la maintenance ou une modification de structure.
Schéma de l'automatisme cycle en "carré" :
Avec un séquenceur, la résolution d'un cycle séquentiel est immédiate. Chaque mouvement ou étape correspond à un module du séquenceur.
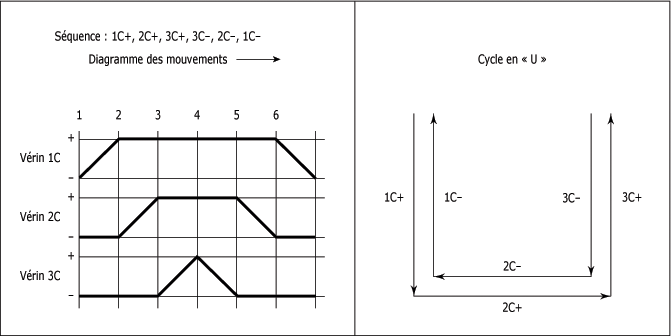
La séquence de vérins à double effet de la figure ci-dessous compte six mouvements. Outre les plaques d'extrémité de tête et de queue, l'ensemble du séquenceur comptera aussi six modules.
Si l'on considère qu'un bouton-poussoir permet de démarrer le cycle, on obtient un séquenceur composé des signaux de commande apparaissant à la figure ci-après.
Cycle en "U" :
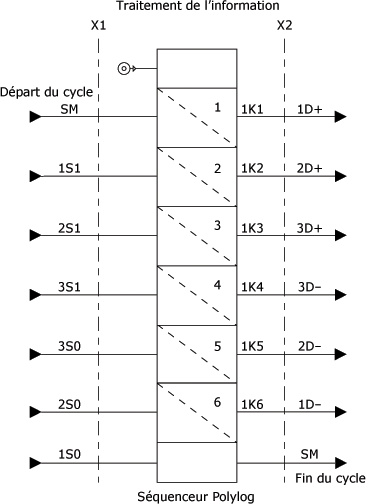
Il suffit ensuite de relier les sorties aux orifices de pilotage des pré-actionneurs pour commander chacun des vérins. Quant à eux, les signaux d'entrée proviennent des capteurs de fin de course qui envoient un signal de retour pour indiquer que le mouvement a été effectué. La figure suivante montre le schéma de cette séquence.
Schéma logique du circuit de l'automatisme cycle en "U" :
Il est à noter que le séquenceur pneumatique ne remplace pas les capteurs de commande (boutons-poussoirs, capteurs à galets…) et les pré-actionneurs.
Le but d'un séquenceur consiste à faire évoluer la séquence dans l'ordre prévu, sans se soucier des chevauchements de signaux. C'est une méthode équivalente à celle des capteurs à commande par galets escamotables et du relais mémoire bistable.
Aucun signal intempestif ou indésirable ne peut perturber le déroulement d'un séquenceur pneumatique. Le séquenceur est donc un outil très efficace pour résoudre un cycle séquentiel et assurer la maintenance. On peut modifier facilement les modes de marche, les modes d'arrêt ou encore ajouter des arrêts d'urgence pour accroître la sécurité.
De plus en plus le séquenceur pneumatique est remplacé par l'automate programmable. Cette technologie s'adapte facilement aux évolutions de la production, elle diminue considérablement le temps de volume d'implantation.
En résumé sur le séquenceur pneumatique :
- Avec un séquenceur pneumatique, la résolution d'un cycle séquentiel devient immédiate.
- Un séquenceur pneumatique a pour fonction de faire se dérouler un cycle séquentiel dans l'ordre prévu, sans se soucier des chevauchements de signaux.
- Un séquenceur gère avec efficacité un système complexe, sans être affecté par les signaux intempestifs ou indésirables comme c'est souvent le cas avec les méthodes des capteurs à commande par galets escamotables et des relais mémoire bistables.
- Il est possible d'effectuer avec simplicité des montages pour des cycles à mouvements simultanés et à mouvements répétés à l'aide d'un séquenceur pneumatique.
- Les orifices de fin de cycle, de début de cycle et de remise à zéro d'un séquenceur permettent de concevoir à peu près toutes les possibilités de modes de marches et d'arrêts.
L'étude portant sur les systèmes séquentiels est terminé. Dans la pratique courante, vous serez parfois en présence de circuits encore plus complexes. Malgré tout, l'approche demeure toujours la même.
Il faut surtout éviter les chevauchements de signaux en appliquant la technique la plus appropriée.
Vous êtes maintenant en mesure de déterminer la méthode la plus propice à utiliser en fonction du problème à résoudre.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !







