Trigonométrie appliquée aux triangles rectangles (2)
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
On appelle cotangente (cotg) la fonction inverse de la tangente.
La cotangente représente donc le rapport entre la mesure du côté adjacent de l'angle de référence et la mesure de son côté opposé.
En termes mathématiques, la cotangente peut s'exprimer de l'une ou l'autre des manières suivantes :
cotg =
ou
ou
.
Les deux exemples qui suivent vous permettront de vous familiariser avec l'application de la fonction tangente.
|
Problème
1:
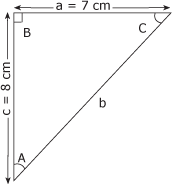
Calculez la valeur décimale de la tangente de l'angle A du triangle de la figure 4.16. Figure 4.16 Triangle 12.
1. Identification des données Sur la figure 4.16, on peut voir que le côté opposé à l'angle A mesure 7 cm tandis que son côté adjacent mesure 8 cm. 2. Calcul de la valeur de la tangente Appliquons la formule de calcul de la tangente :
tg A =
tg A = tg A = 0,8750 La tangente de l'angle A vaut 0,8750. |
|
Problème
2:
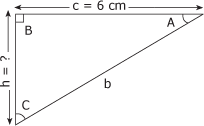
La valeur décimale de la tangente de l'angle A du triangle de la figure 4.17 vaut 0,6666. Calculez la hauteur de ce triangle. Figure 4.17 Triangle 13.
1. Identification des données A partir de l'énoncé du problème et de la figure 4.17, nous pouvons établir que : - tg A = 0,6666 - C.O. = h = ? - C.A. = c = 6 cm 2. Calcul de la valeur du côté h Transformons la formule de calcul de la tangente pour isoler le côté h, qui représente la hauteur du triangle :
tg A =
tg A = devient :
La hauteur du triangle mesure 4 cm. |
La calculatrice constitue un outil précieux pour résoudre des problèmes de trigonométrie.
Elle permet en effet d'obtenir directement la valeur du sinus, du cosinus ou de la tangente d'un angle.

Sinus, cosinus et tangente :
Pour obtenir la valeur d'une des trois fonctions trigonométriques de base pour un angle donné, il suffit :
- d'entrer le chiffre représentant le nombre de degrés de l'angle ;
- d'appuyer sur la touche de la fonction désirée.
Sur plusieurs types de calculatrices, le chiffre représentant le nombre de degrés de l'angle doit être exprimé en nombre décimal plutôt qu'en degrés-minutes-secondes. Dans ce cas, il faut veiller à exprimer les minutes et les secondes en fractions de degrés.
Par exemple, pour exprimer un angle de 30° 30' en nombre décimal, il faut convertir les minutes en degrés : 30' ÷ 60' = 0,5°. La valeur décimale de l'angle de 30° 30' devient alors 30,5°.
Pour trouver la valeur du sinus de l'angle de 30° 30', on doit :
- inscrire sur la calculatrice le chiffre 30,5 ;
- appuyer sur la touche de la fonction sinus.
Certaines calculatrices permettent d'afficher la valeur d'un angle en degrés-minutes-secondes. Dans ce cas, il suffit d'entrer directement la mesure de l'angle et d'appuyer sur la touche de fonction désirée.30,5 sin. = 0,5075.

Mesure d'un angle :
La calculatrice permet aussi d'obtenir la mesure décimale d'un angle à partir de la valeur décimale de son sinus, de son cosinus ou de sa tangente. Pour ce faire, on procède selon les étapes suivantes :
- entrer la valeur décimale du sinus, du cosinus ou de la tangente de l'angle ;
- sélectionner la fonction secondaire (inv ou shift) ;
- appuyer sur la touche de fonction correspondant à la valeur décimale initiale (sin, cos, ou tg).
Si, par la suite, on désire convertir la valeur décimale d'un angle en degrés-minutes-secondes, il suffit d'appuyer sur la fonction secondaire puis sur la touche DMS ou c/d.
L'exemple suivant illustre la manière d'utiliser la calculatrice pour déterminer la valeur d'un angle à partir de la valeur de son sinus.
Consigne particulière de travail, mise en garde ou truc de métier…

Sur plusieurs calculatrices, la fonction secondaire du sinus, du cosinus et de la tangente s'exprime par sin.-1, cos.-1, et tg-1.
|
Problème
La valeur décimale du sinus d'un angle est égale à 0,52324. Quelle est la valeur de cet angle en degrés-minutes-secondes ? 1. Valeur décimale de l'angle Trouvons d'abord la valeur décimale de l'angle correspondant au sinus 0,52324 à l'aide de la calculatrice : 0,52324 inv sin. = 31,54983 2. Valeur de l'angle en degrés-minutes-secondes Tout en conservant la valeur 31,54983 affichée, convertissons-la en notation degrés-minutes-secondes en procédant comme suit : 31,54983 inv DMS = 31,3259 L'angle correspondant au sinus 0,52324 mesure 30° 32' 59". |
Il existe des tables qui donnent la valeur du sinus, du cosinus et de la tangente de plusieurs angles.
Ces tables permettent aussi de déterminer l'angle correspondant à la valeur décimale d'une fonction trigonométrique.
La figure suivante contient l'extrait d'une table trigonométrique.
Table trigonométrique :
|
|
|
|
|
|
Sin. | Cos. |
|
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
0,0698 0,0872 0,1045 0,1219 0,1392 0,1564 0,1736 0,1908 0,2079 0,2250 0,2419 0,2588 0,2756 0,2924 0,3090 0,3256 0,3420 0,3584 0,3746 0,3907 0,4067 0,4226 0,4384 0,4540 0,4695 0,4848 0,5000 0,5150 0,5299 0,5446 0,5592 0,5736 0,5878 0,6018 0,6157 0,6293 0,6428 0,6561 0,6691 0,6820 0,6947 |
0,9998 0,9994 0,9986 0,9976 0,9962 0,9945 0,9925 0,9903 0,9877 0,9848 0,9816 0,9781 0,9744 0,9703 0,9659 0,9613 0,9563 0,9511 0,9455 0,9397 0,9336 0,9272 0,9205 0,9135 0,9063 0,8988 0,8910 0,8829 0,8746 0,8660 0,8572 0,8480 0,8387 0,8290 0,8192 0,8090 0,7986 0,7880 0,7771 0,7660 0,7547 0,7431 0,7314 0,7193 |
0,0175 0,0349 0,0524 0,0699 0,0875 0,1051 0,1228 0,1405 0,1584 0,1763 0,1944 0,2126 0,2309 0,2493 0,2679 0,2867 0,3057 0,3249 0,3443 0,3640 0,3839 0,4040 0,4245 0,4452 0,4663 0,4877 0,5095 0,5317 0,5543 0,5774 0,6009 0,6249 0,6494 0,6745 0,7002 0,7265 0,7536 0,7813 0,8098 0,8391 0,8693 0,9004 0,9325 0,9657 |
45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 |
0,7071 0,7193 0,7314 0,7431 0,7547 0,7660 0,7771 0,7880 0,7986 0,8090 0,8192 0,8290 0,8387 0,8480 0,8572 0,8660 0,8746 0,8829 0,8910 0,8988 0,9063 0,9135 0,9205 0,9272 0,9336 0,9397 0,9455 0,9511 0,9563 0,9613 0,9659 0,9703 0,9744 0,9781 0,9816 0,9848 0,9877 0,9903 0,9925 0,9945 0,9962 0,9976 0,9986 0,9994 0,9998 1,0000 |
0,7071 0,6947 0,6820 0,6691 0,6561 0,6428 0,6293 0,6157 0,6018 0,5878 0,5736 0,5592 0,5446 0,5299 0,5150 0,5000 0,4848 0,4695 0,4540 0,4384 0,4226 0,4067 0,3907 0,3746 0,3584 0,3420 0,3256 0,3090 0,2924 0,2756 0,2588 0,2419 0,2250 0,2079 0,1908 0,1736 0,1564 0,1392 0,1219 0,1045 0,0872 0,0698 0,0523 0,0349 0,0175 0,0000 |
1,0355 1,0724 1,1106 1,1504 1,1918 1,2349 1,2799 1,3270 1,3764 1,4281 1,4826 1,5399 1,6003 1,6643 1,7321 1,8040 1,8807 1,9626 2,0503 2,1445 2,2460 2,3559 2,4751 2,6051 2,7475 2,9042 3,0777 3,2709 3,4874 3,7321 4,0108 4,3315 4,7046 5,1446 5,6713 6,3138 7,1154 8,1443 9,5144 11,43 14,30 19,08 28,64 57,29 
|
Par exemple, pour trouver la valeur du sinus d'un angle de 15° à l'aide de la table, il suffit de :
- repérer, dans la colonne "ANGLE", la valeur de 15° ;
- tirer une ligne horizontale, à partir de cette valeur, jusqu'à la valeur correspondante de la colonne "SIN".
Le point de rencontre donne la valeur du sinus de l'angle de 15°, soit 0,2 588.
En procédant de la même manière, vous pouvez également voir que la tangente valant 0,1763 correspond à un angle de 10°.

C'est à l'Arabe Al
Khwârizmî (780-850) que l'on doit les premières
tables de sinus.
Les premières tables de tangentes ont été le fruit du travail d'un autre Arabe, Habash al Hasib.
Fonctions trigonométriques appliquées à une poulie :
A cette étape, vous devriez être en mesure d'utiliser les notions de trigonométrie pour résoudre des problèmes se rapportant à la mécanique industrielle.
Les exemples qui suivent constituent des problèmes dont la résolution requiert l'application de ces notions.
|
Problème
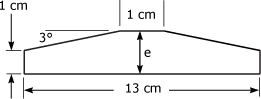
La figure 4.20 représente la vue de profil d'une poulie fabriquée avec un angle de 3°. Calculez l'épaisseur de la paroi "e" de la poulie. Figure 4.20 Vue de profil d'une poulie.
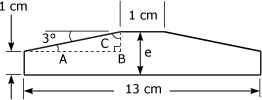
1. Identification des données Pour résoudre le problème, traçons d'abord un triangle rectangle à l'intérieur de la figure 4.21. Figure 4.21 Traçage d'un triangle rectangle.
L'épaisseur de la paroi "e" sera égale à la somme du côté de 1 cm et de la valeur du côté a. Nous devons donc déterminer la valeur du côté a, à l'aide de la fonction tangente. Pour ce faire, nous devons connaître la valeur du côté b. 2. Calcul de la valeur du côté c La mesure du côté b du triangle rectangle sera égale à :
c = c = 6 cm Nous pouvons maintenant tracer le triangle de solution apparaissant à la figure 4.22. Figure 4.22 Triangle de solution.
3. Calcul de la valeur du côté a Puisque la tangente d'un angle représente le rapport entre son côté opposé et son côté adjacent, il est possible d'établir que :
tg 3° =
tg 3° = Isolons maintenant le côté a :
4. Calcul de l'épaisseur de la paroi e Maintenant que nous connaissons la valeur du côté a, nous pouvons calculer l'épaisseur de la paroi "e" en établissant l'équation suivante : e = 1 cm + a e = 1 cm + 0,3144 cm e = 1,3144 cm La paroi "e" a une épaisseur de 1,3144 cm. |
Fonctions trigonométriques appliquées à un profilé :
|
Problème
2 :
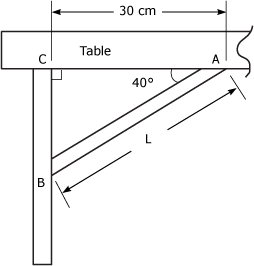
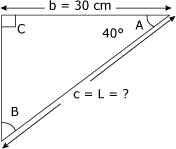
Un mécanicien doit préparer un montage pour le département de soudage afin de faire couper un profilé qui respectera les dimensions indiquées à la figure 4.23. Quelle longueur (L) doit-il attribuer au profilé ? Figure 4.23 Profilé.
1. Identification des données Pour établir clairement le problème, traçons le triangle de solution. Celui-ci apparaît à la figure 4.24. Figure 4.24 Triangle de solution.
Il nous faut donc trouver la valeur de l'hypoténuse (c) de ce triangle, qui correspond à la longueur du profilé. 2. Calcul de la valeur du côté c Utilisons la formule de calcul du cosinus :
cos. 40° =
cos. 40° = Isolons l'hypoténuse :
c =
c = c = 39,162 cm La longueur du profilé devra mesurer 39,162 cm. |
Fonctions trigonométriques appliquées à une plan incliné :
|
Problème
3:
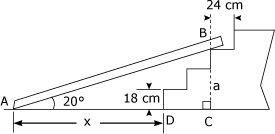
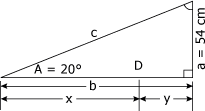
Un plan incliné est installé dans un escalier comme sur la figure 4.25. Calculez la distance x entre le début du plan incliné et le bas de l'escalier. Figure 4.25 Plan incliné.
Pour posséder toutes les données nécessaires à la résolution du problème, nous devons déterminer la valeur du côté a. 1. Calcul de la valeur du côté a Puisque la hauteur de chaque contremarche mesure 18 cm et qu'il y a trois contremarches jusqu'au point de support du plan, le côté a mesure : 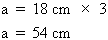
2. Identification des données Nous pouvons maintenant tracer le triangle de solution de la figure 4.26. Figure 4.26 Triangle de solution.
Pour calculer la valeur de x, nous devons déterminer la valeur du côté b et lui retrancher la valeur du segment y. 3. Calcul de la valeur du côté b Calculons la valeur du côté b à l'aide de la définition de la tangente :
tg 20° =
tg 20° = Isolons le côté b :
b =
b = b = 148,36 cm 4. Calcul de la valeur du segment y Puisque chaque marche mesure 24 cm de profondeur, nous pouvons établir que le segment y est égal à :
y = 24 cm y = 48 cm 5. Calcul de la valeur x Nous pouvons maintenant poser l'équation suivante : x = b - y x = 148, 36 cm - 48 cm x = 100,36 cm La distance entre le début du plan incliné et le bas de l'escalier mesure 100,36 cm. |
En résumé sur la trigonométrie appliquée aux triangles rectangles :
A la suite de cette étude, assurez-vous de retenir les points suivants.
- La trigonométrie comporte trois fonctions de base : le sinus, le cosinus et la tangente.
- Les fonctions trigonométriques de base servent uniquement à effectuer des calculs se rapportant aux triangles rectangles.
- Le tableau de la figure suivante contient les principales définitions des fonctions trigonométriques appliquées aux triangles rectangles.
- On peut trouver rapidement la valeur du sinus, du cosinus ou de la tangente d'un angle donné en utilisant la calculatrice ou des tables trigonométriques. De même, ces outils permettent de déterminer l'angle correspondant à une valeur spécifique de sinus, de cosinus ou de tangente.
- Lorsqu'on utilise la calculatrice pour effectuer des calculs trigonométriques, celle-ci doit être en mode angulaire.
Fonctions trigonométriques appliquées aux triangles rectangles :
|
|
|
|
|

|
|
|
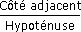
|
|
|
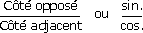
|
|
|
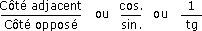
|
Vous savez maintenant utiliser les fonctions trigonométriques de base pour résoudre des problèmes de mécanique dont le triangle de solution est un triangle rectangle.
Mais comment procéder dans le cas de triangles quelconques ? Pour le savoir, poursuivez votre cours.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !


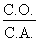 =
= 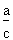
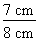
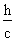
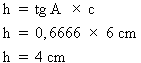
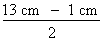
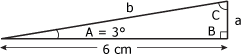
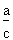
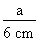
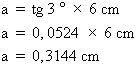
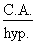 =
= 
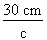
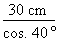
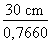
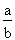
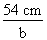
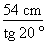
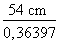
 2
2





