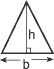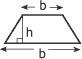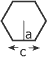Résumé sur la géométrie
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Après avoir effectué les exercices de cette étude, vous devriez être en mesure de résoudre la plupart des problèmes de mécanique industrielle qui se rapportent à la géométrie.
Il apparaît toutefois intéressant de récapituler les notions essentielles contenues dans cette étude.
Résumé sur la géométrie: les Lignes
La géométrie fait appel à des lignes qui portent des noms spécifiques selon leur position, leur orientation ou leur rôle.
Ainsi, on distingue :
- la hauteur : ligne s'élevant de la base d'une figure géométrique jusqu'à l'un de ses sommets en formant un angle de 90° ;
- la bissectrice : ligne partant du sommet d'un angle et le divisant en deux parties égales ;
- la médiane : ligne partant du sommet d'un triangle et se terminant au centre du côté qui lui fait face ;
- la diagonale : ligne qui joint deux sommets non consécutifs d'un quadrilatère ;
- l'arête : point d'intersection entre deux plans.
Résumé sur la géométrie : Les angles
On distingue deux catégories d'angles :
- les angles aigus, compris entre 0° et 90° ;
- les angles obtus, compris entre 90° et 180°.
Certains angles, apparaissant à la figure suivante, portent des noms particuliers en fonction de leur position.
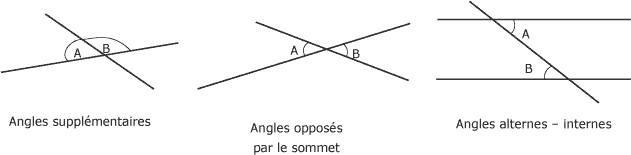
Résumé sur les figures géométriques :
Les triangles sont des figures géométriques simples. Une propriété des triangles veut que la somme de leurs angles intérieurs soit toujours égale à 180°.
De cette propriété, on peut déduire que :
Une autre propriété des triangles est que l'angle extérieur d'un des sommets d'un triangle est égal à la somme des deux angles intérieurs qui ne lui sont pas adjacents.- chaque angle d'un triangle équilatéral (trois angles égaux) mesure 60° ;
- la somme des deux angles qui ne mesurent pas 90° à l'intérieur d'un triangle rectangle (un angle de 90°) est elle aussi égale à 90° ;
- le troisième angle d'un triangle isocèle (2 côtés et deux angles égaux) est égale à 180° moins la somme des deux angles égaux.
Les figures géométriques possédant plus de quatre côtés s'appellent polygones.
On peut diviser les polygones réguliers convexes en un certain nombre de triangles. Ce nombre est égal au nombre de côtés du polygone moins 2.
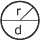
Un cercle est une figure géométrique dont tous les points du contour se situent à égale distance du centre. La circonférence d'un cercle correspond à l'équation suivante :
C = 2πpi.r.
Le diamètre d'un cercle est égal à deux fois le rayon du cercle :
Ø = 2.r.
La valeur d'un arc de cercle peut être déterminée à l'aide de l'équation qui suit :
.
Résumé sur les Aires :
L'aire d'une figure géométrique représente la mesure de la surface comprise à l'intérieur de son périmètre.
Les formules permettant de calculer l'aire des figures géométriques simples apparaissent dans le tableau de la figure suivante.
Aire des figures géométriques simples :
| Figures | Équations | Figures | Équations |
|
Carré
|
A = c2 |
Triangle
|
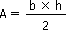
|
|
Rectangle |
A = b 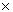 h h
|
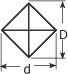
Losange
|
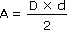
|
|
Parallélogramme
|
A = b 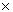 h h
|
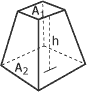
Trapèze
|
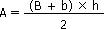
|
|
|
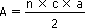
|
Cercle
|
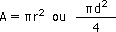
|
Résumé sur les volumes :
Le volume d'une figure géométrique à trois dimensions désigne l'espace qu'elle occupe.
Vous retrouvez, à la figure suivante, les formules permettant de calculer le volume de quelques solides.
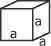
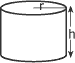
Volume des figures géométriques simples :
|
|
|
|
|
|
|
|
 l l  h h
|
|
|
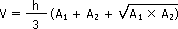
|
|
|
|
C'est avec ce résumé que se termine l'étude consacré à la géométrie.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !