Rapports et proportions cours

Nicolas arrive à la quincaillerie et s'adresse au vendeur : "J'ai besoin d'un câble trois fois plus long que celui-ci".

Pour décrire une caractéristique du câble dont il a besoin, Nicolas l'a comparé à un autre : il a établi un rapport.

En mathématiques, un rapport établit une comparaison entre deux grandeurs de même nature et s'exprime sous forme de fraction.

Par exemple:

Le rapport entre la longueur du câble acheté par Nicolas et celle du câble qu'il a utilisé comme référence s'écrirait 3/1.

• On dit que deux rapports sont inverses lorsque leur produit est égal à 1.

Pour trouver le rapport inverse d'une fraction, il suffit d'inverser le numérateur et le dénominateur.

Par exemple, le rapport inverse de 2/3 est 3/2.

En effet,  2/3  3/2 = 6/6 = 1.

Les rapports sont souvent utiles pour résoudre des problèmes mathématiques, particulièrement lorsqu'il sont exprimés sous forme de proportions.

C'est ce que vous verrez dans cette étude.

Deux rapports qui sont égaux forment une proportion.

Par exemple : les rapports 3/4 et 9/12 forment une proportion.

• Si l'on réduit la fraction 9/12 à sa plus simple expression, on obtient 3/4.

On appelle extrêmes le premier et le quatrième termes d'une proportion ;

les deuxième et troisième termes se nomment moyens. Prenons, par exemple, la proportion suivante :

Dans cette proportion: .

• les nombres 4 et 2 sont les extrêmes ;
• les nombres 1 et 8 sont les moyens.

Propriété fondamentale des proportions :

Les proportions possèdent une propriété particulièrement intéressante pour la résolution de problèmes en mécanique industrielle :

Le produit de leurs extrêmes est égal au produit de leurs moyens.

L'exemple suivant illustre cette propriété fondamentale des proportions.

Application de la propriété des proportions :

Pour savoir si les deux rapports forment une proportion, il suffit d'effectuer la multiplication croisée des extrêmes et des moyens. On obtient alors :

 ;

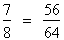7 x 64 = 8 x 56 ;

448 = 448.

Les produits sont égaux. Les rapports forment donc une proportion.

Règle de trois :

La propriété fondamentale des proportions permet de trouver rapidement le terme manquant d'une proportion.

C'est ce que l'on appelle l'application de la règle de trois. Toutefois, soulignons que la règle de trois ne s'applique que lorsque les valeurs du problème varient proportionnellement.

Avant de voir des exemples d'application de la règle de trois, définissons les étapes de résolution de problèmes.

Méthode de résolution de problèmes :

Pour résoudre des problèmes mathématiques, il est intéressant d'acquérir dès le départ une bonne méthode de travail.

Voici les étapes que vous devriez toujours effectuer pour résoudre un problème :

1. Lire l'énoncé du problème.

2. Identifier les données.

3. Exprimer le problème mathématiquement.

4. Effectuer les calculs.

5. Vérifier les résultats.

Dans le cas des problèmes faisant appel à la règle de trois, l'étape 3 consistera à établir la proportion.

L'exemple suivant illustre cette méthode de résolution de problèmes.

Problème :

Le plan d'un atelier de soudage est dessiné à une échelle de 1 cm pour 2 m. Quelle sera la longueur d'un mur qui mesure 3,4 cm sur ce plan ?

1. Lire l'énoncé du problème.

2. Identifier les données.

Nous devons déterminer la longueur réelle du mur qui mesure 3,4 cm sur le plan. Pour ce faire, nous remplacerons la longueur recherchée par la lettre "x".

Longueur réelle du mur : x.

Pour établir la proportion, écrivons le problème sous forme de tableau, en prenant soin de disposer les données de même nature l'une sous l'autre :

3. Écrire le problème mathématiquement

Nous pouvons maintenant établir la proportion suivante :

.

4. Effectuer les calculs

Il ne reste plus qu'à effectuer le produit croisé des termes de la proportion :

 ;

.

x = 6,8 Le mur mesure 6,8 m de longueur.

5. Vérifier le résultat

Pour s'assurer de la validité de la réponse obtenue, il faut effectuer les opérations suivantes :

• refaire les calculs en remplaçant l'inconnue par la valeur calculée ;
• vérifier les unités de mesure utilisées.

Pour valider la réponse obtenue à l'étape précédente, nous devons vérifier si 1/3,4 et 6/20,4 forment une proportion :

 ;

 ;

6,8 = 6,8.

Puisque le produit des extrêmes est égal au produit des moyens, il s'agit bien d'une proportion : 6,8 mètres est donc la bonne réponse.

Le bon sens intervient aussi dans la vérification d'un résultat.

Par exemple, d'après l'énoncé du problème, on peut déduire que le résultat devra être deux fois plus élevé que la donnée représentée par l'échelle de 1 cm.

Règle de trois: suite

Voyons maintenant un exemple illustrant l'application de la règle de trois lorsque

Problème:
La vitesse de rotation d'un engrenage est inversement proportionnelle au nombre de dents de celui-ci. C'est-à-dire que plus l'engrenage possède de dents, moins vite il tourne.

Un train d'engrenages est composé de deux engrenages qui ont respectivement 12 dents et 36 dents. Si la roue du plus petit engrange tourne à une vitesse de 1000 tr/min, à quelle vitesse tournera la roue du plus grand engrenage  ?

1. Lire l'énoncé du problème

2. Identifier les données

Identifions par la variable x, la vitesse de rotation de la roue du grand engrenage. Écrivons les données sous forme de tableau :

3. Écrire le problème mathématiquement

Puisque le rapport entre le nombre de dents et la vitesse de rotation d'un engrenage est inversement proportionnel, nous devons établir la proportion en inversant un des rapports :

.

4. Effectuer les calculs

Effectuons le produit croisé des termes de la proportion :

;

12 x 1000= 36 x X ;

X=333,3.

La roue du grand engrenage tourne donc à 333,3  tr/min.

5. Vérifier le résultat

Déjà, la réponse que nous avons obtenue semble adéquate puisque la vitesse de la grande roue est inférieure et celle de la petite roue.

Vérifions la proportion :

12 x 1000= 36 x 333,3.

12 000 = 12 000.

En arrondissant le résultat, on détermine que 333 tr/min est donc la réponse exacte.

Pourcentages :

Le pourcentage indique un rapport exprimé sur cent.

De nombreuses valeurs peuvent s'exprimer en pourcentage :

• l'intérêt,
• le taux d'inclinaison d'une pente,
• le rendement d'une machine,
• le salaire, etc.

Le symbole % sert à exprimer un pourcentage.

Pour exprimer un pourcentage sous forme décimale, on le divise par 100.

Par exemple :

95 % = 95 ÷ 100 = 0,95.

Inversement, pour exprimer un nombre sous forme de pourcentage, on le multiplie par 100.

Par exemple :

0,75 = 0,75  100 = 75 %.

La transformation d'un pourcentage en fraction permet souvent d'effectuer un calcul plus rapidement.

60 % =  = .

Calcul de la valeur correspondant à un pourcentage :

Pour calculer la valeur correspondant au pourcentage d'un nombre, on fait appel à la règle de trois.

L'exemple qui suit montre comment procéder.

Calculez la valeur correspondant à 7 % de 490.

1. Écriture du problème sous forme de proportion

On peut exprimer 7 % de 490 sous la forme de la proportion suivante :

 = .

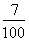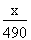2. Calcul de la valeur correspondant au pourcentage

Il ne reste plus qu'à résoudre l'équation à l'aide de la règle de trois :

=  ;

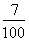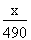100 x X= 7 x 490 ;

X =  ;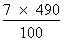

X = 34,3.

7 % de 490 est égal à 34,3.

Calcul d'un pourcentage :

Pour résoudre des problèmes visant à définir une valeur sous forme de pourcentage, il faut suivre deux étapes :

L'exemple qui suit illustre cette méthode de résolution.

Vous achetez un home cinéma dont le prix s'élève à 2 850 €. Le montant total inscrit sur la facture est de 3408,60 €.

Calculez le pourcentage de taxes que vous avez payé sur le home cinéma.

1. Calcul du montant de taxes

Pour connaître le montant de taxes payées, il suffit de soustraire le prix du home cinéma du montant total à payer :

3408,60 € - 2850 € = 558,60 €.

2. Calcul du pourcentage de taxes

Trouvons maintenant la proportion de taxes payées :

558,60/2850 = 0,196.

Exprimons ce nombre décimal sous forme de pourcentage :

0,196*100=19,6 %.

Vous avez donc payé 19,6 % de taxes sur le montant total de la facture (TVA).