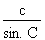L'application de notions de mathématiques
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Dans ce module sur les mathématiques appliquées, vous avez révisé des notions de mathématiques.
Vous avez aussi appliqué ces notions à la résolution de problèmes se rapportant à la mécanique industrielle.
Dans l'étude sur l'application de notions de mathématiques, vous aurez l'occasion de faire le point sur l'ensemble des éléments présentés dans ce module.
Vous y retrouverez :
- Un résumé complet des notions exposées ;
- Une activité de synthèse qui vous permettra d'évaluer l'état de vos connaissances.
- Une brève conclusion ;
- Une bibliographie complètant l'étude sur l'application de notions de mathématiques.
Résumé les mathématiques appliquées :
Dans cette étude, vous retrouverez le résumé de chacune des études sur les mathématiques appliquées.
Sa lecture vous permettra de vérifier si vous avez retenu les points importants exposés dans ce module.
Si vous ne comprenez pas entièrement certains sujets énumérés dans le résumé, n'hésitez pas à reprendre la lecture d'une partie du module ou à refaire un exercice.
Résumé sur le système de mesure :
|
• Le système international est un système décimal, possédant sept unités de base dont les principales sont:
|
|
|
• Le système de mesure utilise des multiples et des sous-multiples des unités de base afin d'exprimer des grandeurs variées.
|
Résumé sur les mathématiques de base :
• Lorsque l'on effectue des opérations de base sur des entiers, des fractions ou des nombres décimaux, il faut porter une attention particulière à la loi des signes.
Le tableau de la figure suivante synthétise cette loi.
Loi des signes :
|
|
|
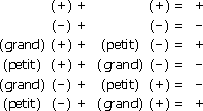
|
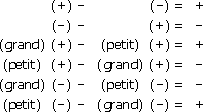
|
|
|
|
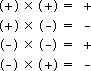
|
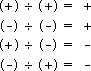
|
• Pour faire la somme ou la différence de deux fractions, elles doivent d'abord posséder sur un dénominateur commun puis additionner ou soustraire les numérateurs.
• Pour faire le produit de deux fractions, il suffit de multiplier les numérateurs puis de multiplier les dénominateurs.
• Le quotient de deux fractions s'obtient en inversant la deuxième fraction puis en faisant le produit des fractions.
• L'addition ou la soustraction de nombres décimaux s'effectue en alignant la virgule décimale.
• Le produit de deux nombres décimaux s'effectue sans tenir compte de la virgule. On place ensuite la virgule de sorte que le produit compte autant de chiffres après la virgule qu'il y en a dans tous les facteurs réunis.
• Pour diviser un nombre décimal par un autre, on doit d'abord transformer les deux nombres en nombres entiers.
• Dans une proportion, le produit des moyens est égal au produit des extrêmes.
• Avant de résoudre une expression algébrique, il est préférable de la réduire, c'est-à-dire d'effectuer toutes les opérations possibles sur les termes identiques.
• Pour transposer un terme d'un membre à l'autre dans une équation, il suffit d'effectuer l'opération inverse.
• Pour résoudre une équation algébrique, on doit :
- réduire les expressions algébriques ;
- isoler la variable et déterminer sa valeur ;
- substituer la valeur trouvée dans l'équation afin de vérifier le résultat.
• La résolution d'une équation algébrique à deux variables exige que l'on connaisse au moins deux équations, de manière à procéder par substitution. o
Résumé sur la géométrie :
|
• Le périmètre représente la mesure du contour d'une figure géométrique à deux dimensions. |
|
|
• L'aire est la mesure de la surface d'une figure géométrique. |
|
|
• Le volume représente l'espace occupé par une figure géométrique à trois dimensions. |
|
|
• Les applications mécaniques de la géométrie se rapportent surtout à l'aire et au volume des figures géométriques. Les formules permettant de calculer l'aire et le volume des figures géométriques simples apparaissent aux figures suivantes de ce module. |
Aire des figures géométriques simples :
| Figures | Équations | Figures | Équations |
|
Carré
|
A = c2 |
Triangle
|
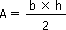
|
|
Rectangle |
A = b 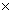 h h
|
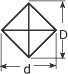
Losange
|
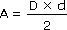
|
|
Parallélogramme
|
A = b 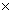 h h
|
Trapèze
|
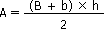
|
|
|
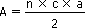
|
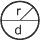
Cercle
|
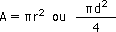
|
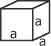
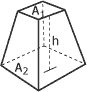
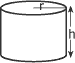
Volume des figures géométriques simples :
|
|
|
|
|
|
|
|
 l l 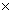 h h
|
|
|
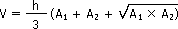
|
|
|
|
Résumé sur la trigonométrie :
|
• La trigonométrie appliquée aux triangles rectangles se fonde sur trois fonctions de base :
|
|
|
• La résolution de problèmes se rapportant aux triangles quelconques fait appel à deux lois :
|
|
|
• La loi des sinus peut s'exprimer mathématiquement de la manière suivante :
|
|
|
• La loi des cosinus permet d'établir les relations suivantes :
|
Résumé sur les tables et les abaques
|
• Les tables et les abaques servent à déterminer des valeurs sans avoir à effectuer tous les calculs qui s'y rapportent. |
|
|
• Avant d'utiliser une table ou un abaque, on doit :
|
Vous avez bien saisi les points importants du résumé général ? Si c'est le cas, passez à l'activité synthèse.
Conclusion :
Le module est maintenant terminé.
Vous y avez revu des notions de mathématiques dont vous vous servirez tout au long de votre formation, puis durant votre activité professionnelle.
Comme vous avez pu le constater, les mathématiques permettent de résoudre rapidement des problèmes reliés à la mécanique :
- problèmes d'hydraulique,
- de pneumatique,
- d'électricité, etc.
En étudiant les autres cours de votre programme de formation, vous comprendrez l'origine de plusieurs formules de calcul que vous avez appliquées. De même, vous découvrirez d'autres formules qui vous permettront de trouver la solution à des problèmes divers.
Pour le moment, il importe surtout que vous maîtrisiez suffisamment les diverses opérations mathématiques de base pour les utiliser avec souplesse et efficacité.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !



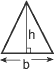


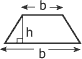
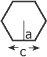

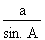 =
= 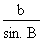 =
=