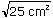Figures géométriques introduction (1)
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
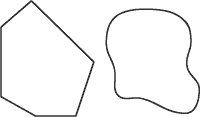
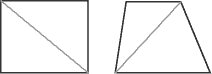
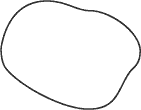
On peut définir une figure géométrique comme un espace limité par des segments de droite ou par une ligne continue, telle une ligne courbe.
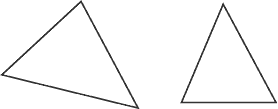
La figure suivante montre deux figures géométriques.
Les figures géométriques possèdent des caractéristiques et des propriétés particulières.
Pour résoudre des problèmes de mécanique qui font appel à la géométrie, vous devez connaître ces propriétés.
Dans cette étude, vous étudierez les figures géométriques de base et leurs propriétés.
Si vous possédiez une loupe assez puissante, vous verriez qu'une ligne se compose d'une suite de points très rapprochés les uns des autres.
On distingue plusieurs types de lignes, portant des noms spécifiques selon leur position ou leur orientation dans l'espace, ou encore selon leur fonction.
Les principales lignes utilisées en géométrie apparaissent à la figure suivante.
Principales lignes utilisées en géométrie :
|
Noms |
Descriptions |
Exemples |
|
Parallèles |
Lignes dont les points ne se rencontrent jamais, même si on les prolonge à l'infini. |
|
|
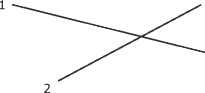
Sécantes ou concourantes |
Lignes dont les points se rencontrent dans l'espace. |
|
|
Hauteur |
Ligne s'élevant de la base d'un angle et le divisant en deux parties égales. |
|
|
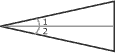
Bissectrice |
Ligne partant du sommet d'un angle et le divisant en deux parties égales. |
|
|
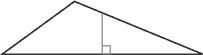
Médiane |
Ligne menée du sommet d'un triangle au centre du côté qui lui fait face (coté opposé). |
|
|
Médiatrice |
Ligne s'élevant perpendiculairement (à 90°) à un point situé au milieu du côté d'un triangle. |
|
|
Diagonale |
Ligne joignant deux sommets non consécutifs d'un quadrilatère. |
|

Notes: deux lignes se rapportent spécifiquement à la géométrie dans l'espace :
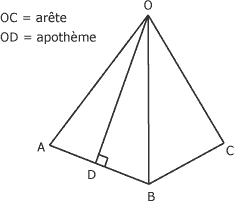
- l'arête, qui constitue une ligne d'intersection entre deux plans ;
- l'apothème, qui est une ligne joignant le sommet d'une pyramide ou d'un cône à un point de sa base en formant un angle de 90° (figure suivante).
Arête et apothème :
Le périmètre représente la somme de la longueur des segments de droite qui délimitent un espace.
Plus simplement, on peut dire que le périmètre constitue la longueur du contour d'une surface.
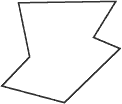
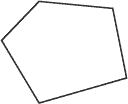
Un périmètre peut prendre trois formes distinctes :
- convexe,
- concave,
- courbe.
Vous pouvez voir ces trois formes de périmètres à la figure suivante.
Périmètres :
|
||||||||||||||||||||||||||||||||||||
Le terme angle désigne l'ouverture variable entre deux segments de droites concourantes ou sécantes.
On peut diviser les angles en deux catégories :
- les angles aigus, dont l'ouverture se situe entre 0° et 90° ;
- les angles obtus, dont l'ouverture varie entre 90° et 180°.
Angles aigus et obtus :
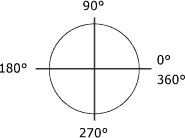
Certains angles sont remarquables. C'est le cas des angles de 0°, 90° (angle droit), 180° (angle plat), 270° et 360°, qui apparaissent à la figure suivante.
Angles remarquables :
Propriétés des angles :
Les angles possèdent des propriétés particulières.
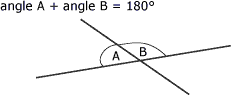
Ainsi, lorsque deux droites se coupent, la somme des angles adjacents, c'est-à-dire des angles possédant un côté commun, égale 180°. On dit alors qu'il s'agit d'angles supplémentaires (figure suivante).
Angles supplémentaires :
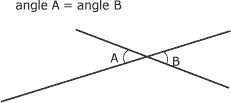
D'autre part, deux droites qui se coupent forment des angles opposés par le sommet, dont la valeur est égale (figure suivante).
Angles opposés par le sommet :
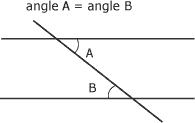
Enfin, un segment de droite qui coupe deux segments de droites parallèles forme avec ceux-ci des angles alternes-internes égaux (figure suivante).
Angles alternes-internes :
La figure géométrique la plus simple est limitée par trois segments de droite :
- il s'agit du triangle (figure suivante).
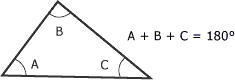
Une des propriétés fondamentales des triangles est que la somme de leurs angles intérieurs égale 180°.
Somme des angles intérieurs d'un triangle :
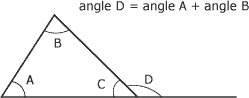
Autrepropriété l'angle extérieur d'un des sommets d'un triangle est égal à la somme des deux angles intérieurs qui ne lui sont pas adjacents.
Valeur de l'angle extérieur du sommet d'un triangle :
Ces propriétés s'appliquent à tous les triangles.
Les triangles particuliers :
Comme vous vous en souvenez sans doute, certains triangles portent des noms spécifiques en fonction de leurs caractéristiques particulières.
La figure suivante dresse la liste de ces caractéristiques.
Caractéristiques des triangles :
|
Noms |
Descriptions |
Exemples |
|
Quelconque |
Côtés et angles pas égaux |
|
|
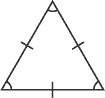
Équilatérale |
3 angles et 3 côtés égaux |
|
|
Rectangle |
Un angle de 90° |
|
|
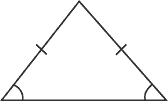
Isocèle |
2 côtés égaux et 2 angles égaux |
|
Le théorème de Pythagore :
Les triangles rectangles possèdent des propriétés particulières.
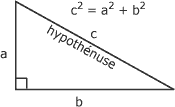
Une de ces propriétés est connue sous l'appellation de théorème de Pythagore (figure suivante).
|
Ce théorème s'énonce comme suit : La somme des carrés des côtés d'un triangle rectangle est égale au carré de son hypoténuse. Mathématiquement, cet énoncé s'exprime ainsi : |
Voyons comment appliquer le théorème de Pythagore à l'aide d'un exemple.
|
Problème
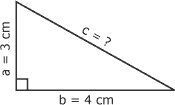
Calculez la valeur de l'hypoténuse du triangle rectangle de la figure suivante. Hypoténuse d'un triangle rectangle :
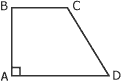
1. Identification des données Sur la figure 3.19, on constate que les côtés du triangle rectangle mesurent respectivement 3 cm et 4 cm. 2. Calcul de la valeur de l'hypoténuse Pour trouver la valeur de l'hypoténuse, il suffit d'appliquer la formule du théorème de Pythagore : c2 = a2 + b2 c2 = 32 + 42 c2 = 9 cm2 + 16 cm2
c2 = c2 = 5 cm L'hypoténuse est égale à 5 cm. |
La figure géométrique qui suit en complexité le triangle est le quadrilatère ou polygone à quatre côtés.
Les quadrilatères se divisent en deux grandes classes : les parallélogrammes et les trapèzes (figure suivante).
Quadrilatères :
 Parrallélogramme Parrallélogramme
|
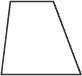 Trapèze Trapèze
|
Un trapèze est un quadrilatère dont deux des côtés opposés sont parallèles (figure suivante).
Il est possible de diviser les trapèzes en deux catégories :
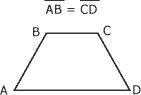
- Le trapèze isocèle lorsque les deux côtés qui ne sont pas parallèles sont égaux.
- Le trapèze rectangle lorsqu'un des côtés non parallèle du trapèze est perpendiculaire aux deux bases parallèles.
Trapèzes :
|
Trapèze isocèle |
BC parallèle à AD |
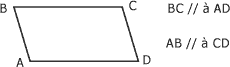
Le parallélogramme est un quadrilatère dont les côtés opposés sont parallèles (figure suivante).
Parallélogramme :
La diagonale divise toujours un parallélogramme en deux triangles égaux et opposés (figure suivante).
Division du parallélogramme à l'aide d'une diagonale :
On distingue trois parallélogrammes particuliers, apparaissant à la figure suivante :
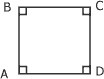
- le rectangle, qui possède quatre angles de 90° ;
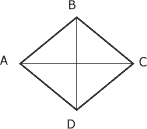
- le losange, dont les côtés sont égaux, mais dont les sommets forment des angles différents de 90° ;
- le carré, dont les côtés sont égaux et qui possède quatre angles de 90°.
Parallélogrammes particuliers :
|
Rectangle avec: BC // à AD et AB // à CD |
Losange avec: AB // à DC et BC // à AD |
Carré avec: BC // à AD et AB // à CD |

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !