Algèbre de Boole
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Toute algèbre est composée de deux éléments : les variables et les opérateurs. Dans l'algèbre conventionnelle, les variables sont les nombres et les opérateurs sont l'addition, la soustraction, la multiplication et la division.
L'algèbre de Boole est, elle aussi, constituée de variables dites "booléennes" et d'opérateurs.
Variables booléennes :
Une variable booléenne est une quantité logique qui n'admet que deux états possibles : "VRAI" ou "FAUX".
L'état logique "VRAI" est symbolisé par 1. Il indique que la variable est à un niveau logique "HAUT", c'est-à-dire qu'elle existe et qu'elle est bien présente.Dans la pratique, un niveau "HAUT" peut signifier une tension de 5 V ou un contact fermé.
L'état logique "FAUX" désigne l'inverse, c'est-à-dire que la variable est absente. Elle est alors symbolisée par 0. Un contact ouvert qui ne laisse pas passer le courant ou une tension de 0 V sont des exemples de variables booléennes d'un niveau logique "BAS".
Ceci est semblable à la notion des bits du système binaire que vous avez étudié dans l'étude sur les systèmes de numérotation et de codage. En effet, une variable booléenne peut être représentée par un bit qui est égal à 0 ou à 1. Dans la pratique, ces variables sont symbolisées par les lettres de l'alphabet. Par exemple, un vérin peut être désigné par la lettre C et un moteur par la lettre M.
Opérateurs de l'algèbre Booléenne :
Trois opérateurs logiques ont été définis par Georges Boole. Ce sont les façons de combiner les variables booléennes entre elles. Il s'agit de :
- l'addition,
- la multiplication,
- la négation.
Addition Booléenne "+"
Cet opérateur défini l'addition dans l'algèbre de Boole. Le symbole logique de cet opérateur est "OU". Le tableau de la figure suivante montre l'ensemble des combinaisons possibles et le résultat correspondant de l'opération logique "OU" pour deux variables booléennes a et b.
Opérateur "OU" :
| a |
|
|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Le résultat de l'addition booléenne prend la valeur 0 si les deux variables additionnées ont simultanément l'état logique 0. Il prend la valeur 1 si l'une des deux variables au moins ou les deux simultanément ont l'état logique 1.
Le tableau de la figure ci-dessus est appelé la table de vérité de l'opérateur "OU". Dans le cas général, la table de vérité d'une fonction logique est la compilation sous forme de tableau de l'état logique de la variable de sortie par rapport aux états logiques des variables d'entrée.
Multiplication booléenne "·"
Le symbole logique de cet opérateur est "ET". Pour deux variables booléennes, le résultat de cette opération est 0 si une variable ou les deux sont à l'état logique 0. Le résultat 1 est obtenu quand les deux variables d'entrée sont à l'état logique 1. Le tableau de la figure 2.2 présente toutes ces possibilités.
Opérateur "ET" :
| a |
|
|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Opérateur "NON"
Cet opérateur s'applique à une
seule variable booléenne et il donne la négation de
cette variable. Si une variable a est à l'état
logique 1, le "NON A" qui est noté 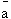 (prononcez a barre) est à l'état
logique 0. La négation d'une variable booléenne
est l'opposé ou le négatif de cette variable. Le
tableau de la
figure suivante contient
l'ensemble des possibilités lorsque cet opérateur est
appliqué à une variable booléenne a.
(prononcez a barre) est à l'état
logique 0. La négation d'une variable booléenne
est l'opposé ou le négatif de cette variable. Le
tableau de la
figure suivante contient
l'ensemble des possibilités lorsque cet opérateur est
appliqué à une variable booléenne a.
Opérateur "NON" :
|
|
|
| 0 | 1 |
| 1 | 0 |
Supposez plusieurs propositions indépendantes. Une décision prise en fonction d'un arrangement de ces propositions fait en sorte que la décision est une fonction logique de ces propositions. Plus simplement, la décision est une fonction logique alors que les propositions sont les variables indépendantes du problème. Voici un exemple d'une fonction logique.
On veut contrôler le départ d'une course. Deux contrôleurs sont responsables du départ :
- a = contrôleur n° 1
- b = contrôleur n° 2
Le départ a lieu si 1 contrôleur est prêt. En terme d'opérateur logique, une variable est remplacée par son nom quand elle est "fausse". Le départ sera donné :
- si le contrôleur n° 1 est prêt donc a = "vraie" et b = "fausse".
- ou si le contrôleur n° 2 est prêt donc b = "vraie" et a = "fausse".
Ainsi la fonction départ
s'écrit : 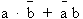 .
.
L'algèbre booléenne dispose d'un ensemble de lois, de postulats et de théorèmes fondamentaux qui définissent les règles de base de la combinaison des variables booléennes.
Postulats :
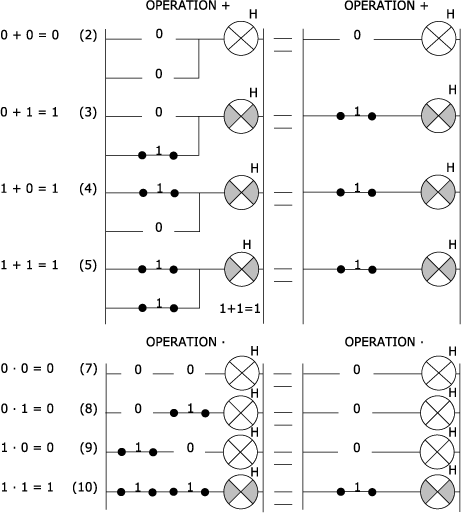
Les postulats sont les exigences et les conditions relatives à chacun des opérateurs de l'algèbre booléenne. Ils forment un ensemble de 10 règles qui régissent les opérateurs "OU", "ET" et "NON". Le tableau de la figure ci-dessous et les schémas de la figure ci-après les présentent.
Postulats de l'algèbre booléenne :

Théorèmes de base pour une seule variable booléenne :
Un ensemble de théorèmes s'appliquent à une seule variable booléenne en présence des opérateurs "OU", "ET" et "NON". Ce sont les théorèmes de l'identité et ils apparaissent au tableau des figures suivantes.
Théorèmes pour une seule variable :
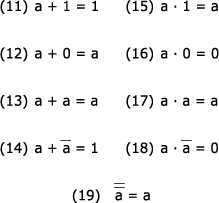
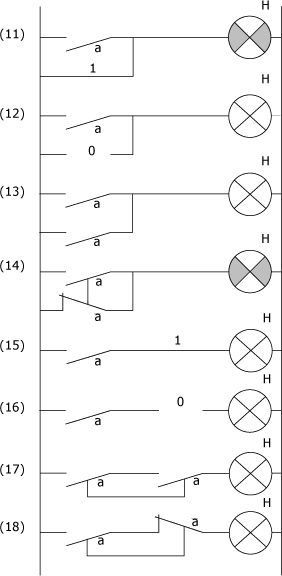
L'ensemble des théorèmes pour une seule variable booléenne présentés dans le tableau de la figure ci-dessus peuvent être démontrés un à un de la manière suivante.
Étant donné que a est une variable booléenne, elle ne peut admettre que deux valeurs soient 0 ou 1. Pour démontrer un théorème, il faut remplacer la variable par 0 ou 1 et examiner si le résultat obtenu est conforme à l'énoncé de cette loi.
(11)
- Si a = 0 ; alors a + 1 = 0 + 1 = 1 d'après le postulat (3).
- Si a = 1 ; alors a + 1 = 1 + 1 = 1 d'après le postulat (5).
Donc a + 1 = 1 est vrai pour toute variable booléenne a.
(12)
- Si a = 0, alors a + 0 = 0 + 0 = 0 d'après le postulat (2).
Or a = 0, donc a + 0 = 0 = a.
- Si a = 1, alors a + 0 = 1 + 0 = 1 d'après le postulat (4).
Or a = 1, donc a + 0 = 1 = a.
Donc a + 0 = a est vrai pour toute variable booléenne.
(13)
- Si a = 0, alors a + a = 0 + 0 = 0 d'après le postulat (2).
Comme a = 0, alors a + a = 0 = a.
- Si a = 1, alors a + a = 1 + 1 = 1 d'après le postulat (5).
Comme a = 1, alors a + a = 1 = a.
Donc a + a = a est vrai pour toute variable booléenne.
(14)
- Si a = 0, alors
d'après le postulat (1).
Donc
d'après le postulat (3).
- Si a = 1, alors
d'après le postulat (6).
Donc
d'après le postulat (4).
L'énoncé
est donc vrai pour toute variable booléenne.
(15)
- Si a = 0, a • 1 = 0 • 1 = 0 d'après le postulat (8).
Comme a = 0, alors a • 1 = 0 = a.
- Si a = 1, a • 1 = 1 • 1 = 1 d'après le postulat (10).
Comme a = 1, alors a • 1 = 1 = a.
Donc pour toute variable booléenne a, a • 1 = a.
(16)
- Si a = 0, alors a • 0 = 0 • 0 = 0 d'après le postulat (7).
- Si a = 1, alors a • 0 = 1 • 0 = 0 d'après le postulat (9).
Donc l'énoncé a x 0 = 0 est vrai pour toute variable booléenne.
(17)
- Si a = 0, alors a • a = 0 • 0 = 0 d'après le postulat (7).
Comme a = 0, donc a • a = 0 = a.
- Si a = 1, alors a • a = 1 • 1 = 1 d'après le postulat (10).
Comme a = 1, donc a • a = 1 = a.
Donc pour toute variable booléenne a, a • a = a.
(18)
- Si a = 0,
d'après le postulat (1).
Donc a • 1 = 0 • 1 = 0 d'après le postulat (8).
· Si a = 1, alors
d'après le postulat (6).
Donc
d'après le postulat (9).
L'énoncé
est donc vrai pour toute variable booléenne.
(19)
· Si a = 0, alors
d'après le postulat (1) et
d'après le postulat (6).
Comme a = 0, alors
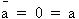
· Si a = 1, alors
d'après le postulat (6) et
d'après le postulat (1).
Comme a = 1, alors
.
Lois pour plusieurs variables booléennes :
Ces lois définissent les règles de commutativité, d'associativité et de distributivité pour les opérateurs "OU" et "ET" en présence de trois variables booléennes. Le tableau de la figure suivante présente l'ensemble de ces lois.
| LOI DE COMMUTATIVITÉ (Loi d'échange) | |
| (20) a + b = b + a | (21) a · b = b · a |
| LOI D'ASSOCIATIVITÉ (Loi de liaison) | |
| (22) a + (b + c) = (a + b) + c = a + b + c | (23) a · (b · c) = (a· b) · c = a · b · c |
| LOI DE DISTRIBUTIVITÉ (Loi de répartition) | |
| (24) (a + b) · (b + c) = (a · b) + (a · c) + (b · b) + (b · c) | (25) a · (b + c) = (a · b) + (a · c) |
- Les lois (20) et (21) indiquent que les opérations logiques "OU" et "ET" sont des lois de compositions commutatives ; l'ordre de l'addition ou de la multiplication logique n'a pas d'importance.
- Les lois (22) et (23) concernent la propriété de l'associativité. Les variables d'une addition logique ou d'une multiplication logique peuvent être groupées de plusieurs manières.
- La loi (24) montre que, comme dans l'algèbre ordinaire, la multiplication logique est distributive par rapport à l'addition logique. Une expression peut, en effet, être développée par la multiplication logique des termes un à un.
- La loi (25) concerne la distributivité de l'addition logique par rapport à la multiplication logique. La multiplication logique dans une expression peut être remplacée par l'addition logique de toutes les multiplications des termes un à un.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !







