Vibrations mécaniques (1)
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Acquérir une connaissance fondamentale de la vibration est la première étape d'un apprentissage où vous allez vous familiariser avec l'usage de l'outil "vibration" en maintenance.
Il faut d'abord en donner une définition. Vous allez commencer par apprendre à décrire le phénomène en termes d'amplitude, de fréquence et de phase à l'aide d'un modèle simple. Vous allez ensuite poursuivre votre apprentissage avec l'étude des caractéristiques vibratoires d'une machine.
La vibration est un phénomène dynamique, c'est-à-dire en mouvement. L'étude des mouvements périodiques et, plus particulièrement, du mouvement oscillatoire conduit à une définition de la vibration.
Parmi les mouvements mécaniques les plus variés qui se produisent autour de vous, il existe souvent des mouvements qui se répètent. Pensez au battement de votre cœur, au mouvement d'une balançoire, au passage des pales d'un ventilateur de plafond ou encore au mouvement alternatif des pistons d'un moteur à explosion. Tous ces mouvements ont un trait commun : une répétition d'un même cycle de mouvements.
Un cycle est une suite ininterrompue de mouvements ou de phénomènes qui se renouvellent toujours dans le même ordre. Prenez à titre d'exemple le cycle à quatre temps d'un moteur à explosion. Un cycle complet comprend quatre étapes (admission, compression, explosion, échappement) qui sont toujours réalisées dans le même ordre.
On appelle mouvement périodiqueun mouvement qui se répète et dont chaque cycle se reproduit identiquement. La durée d'un cycle est appelée période.
Un mouvement périodique particulièrement intéressant dans le domaine de la mécanique est celui d'un objet qui se déplace de sa position d'équilibre et y revient en effectuant un mouvement de va-et-vient par rapport à cette position.
Ce type de mouvement périodique se nomme oscillation ou mouvement oscillatoire. Les oscillations d'une masse reliée à un ressort, le mouvement d'un pendule ou les vibrations d'un instrument à corde sont des exemples de mouvements oscillatoires.
On appelle vibration le phénomène dynamique qui décrit un objet animé d'un mouvement oscillatoire. L'objet en question peut être une machine ou un de ses composants dont la position d'équilibre est souvent définie comme la position au repos.
Une introduction aux caractéristiques fondamentales de la vibration s'impose. Votre apprentissage de l'outil "vibration" exige que vous connaissiez les notions de base en vibration et le vocabulaire qui s'y rattache.
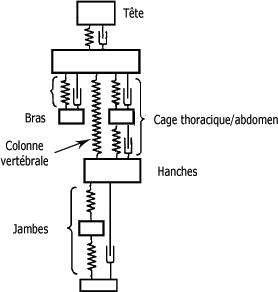
Tout système mécanique, incluant les machines industrielles les plus complexes, peut être représenté par un ou plusieurs systèmes composés d'un ressort, d'un amortisseur et d'une masse. Le corps humain, souvent qualifié de "belle mécanique", est décomposé à la figure suivante en plusieurs sous-systèmes "masse-ressort-amortisseur" représentant la tête, les épaules, la cage thoracique, etc.
Système mécanique complexe :
Théoriquement, si une masse reliée à un ressort est mise en mouvement, la masse oscille - mouvement de va-et-vient autour de sa position d'équilibre stable (masse au repos) - sans jamais s'arrêter.
Pour vous aider à mieux visualiser le déplacement de cette masse dans le temps, imaginez un mécanisme simple comme celui que montre la figure ci-après. Il consiste en une bande de papier qui défile à vitesse constante dans une direction perpendiculaire au mouvement de la masse. Une plume attachée à la masse en mouvement trace sur le papier une ligne ondulée de forme régulière.
Le tracé de la figure ci-après correspond en tout point au tracé d'une courbe sinusoïdale. Pour cette raison, on appelle mouvement sinusoïdalle mouvement oscillatoire décrit par un système "masse-ressort". L'oscillation sinusoïdale est aussi appelée mouvement harmonique simple ou oscillation harmonique. Elle peut être décrite en fonction de son amplitude et de sa fréquence.
Vibration d'un système "masse-ressort" :
En vous reportant à la figure suivante, remarquez l'axe t (temps) qui représente la droite que la plume tracerait si la masse était immobile. L'axe d (déplacement) représente, quant à lui, la position de la masse en un temps donné.
Description de la courbe sinusoïdale :
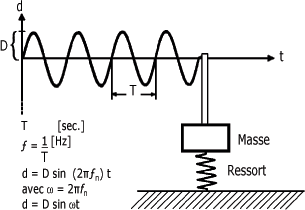
Pour un mouvement sinusoïdal, la position de la masse varie en fonction du temps selon l'expression d = Dsin2πfnt où D représente l'amplitude de crête de la vibration du système "masse-ressort". L'amplitude définit ici le déplacement maximal, plus couramment appelé déplacement de crête ou encore déplacement de crête à crête de la masse qui oscille par rapport à l'axe t.
La période d'oscillation est représentée par T qui est égale au temps requis à la plume pour parcourir un cycle complet. Le nombre de cycles complets effectués en une seconde est appelé fréquence (f). L'unité de fréquence est le cycle par seconde ou hertz (Hz). On utilise aussi le cycle par minute ou CPM qui n'est autre que 60 · Hz.
Si la période d'un système "masse-ressort" est égale à 0,5 s, deux cycles s'effectuent en 1 s et la fréquence du système est égale à 2 Hz. En notant T la durée d'une période en secondes et f la fréquence en hertz, on peut écrire la relation suivante : fréquence = 1/période ou f = 1/T.
Notez bien qu'une telle relation entre la fréquence et la période ne s'applique qu'au mouvement sinusoïdal.
La notion de phase en vibration peut se résumer en trois mots : "comment ça bouge". La phase est la position d'une pièce en vibration à un moment donné, en référence à un point fixe ou à une autre pièce en vibration. En pratique, la mesure de phase est un moyen simple de comparer un mouvement vibratoire à un autre, c'est-à-dire de déterminer comment une pièce vibre ou "bouge" relativement à une autre.
La mesure de phase est normalement exprimée en degrés (un cycle complet de vibration est égal à 360°.
Imaginez deux masses qui vibrent à la même amplitude et à la même fréquence. Peut-il exister une différence entre ces deux mouvements vibratoires ? La réponse est oui.
La figure ci-dessous montre deux masses identiques suspendues chacune à un ressort. Elles ont été déplacées de leur position d'équilibre dans le même sens et en parcourant une distance égale dans les deux cas. Il suffit de les relâcher en même temps pour obtenir deux vibrations harmoniques de même amplitude et de même fréquence.
Comme vous pouvez le constater, rien ne saurait à première vue les différencier l'une de l'autre. On dit de ces masses qu'elles vibrent en phase.
Masses vibrant en phase :
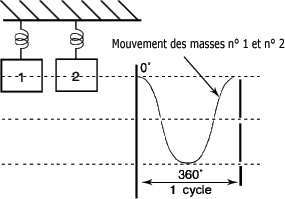
Qu'arrive-t-il si les masses sont relâchées à des instants différents ? Les vibrations sont décalées dans le temps. Ce phénomène s'appelle le déphasage. Un déphasage nul signifie que les vibrations sont en phase ou ont une même phase. Un déphasage de 180° signifie que les vibrations sont à 180° hors-phase (opposition de phase). Un tel cas vous est montré à la figure suivante où les masses ont été déplacées en parcourant une même distance, mais dans un sens opposé.
Masses vibrant à 180° hors-phase :
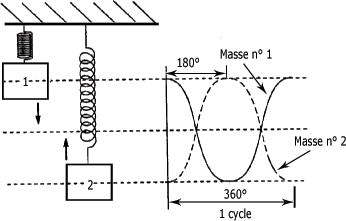
La mesure de phase est d'un grand intérêt dans le domaine de l'analyse des vibrations appliquées à la surveillance des machines. Il est essentiel que vous compreniez bien la notion de phase avant de poursuivre votre apprentissage.
La vibration de tout système "masse-ressort" considéré jusqu'à présent est obtenue par le déplacement de la masse de sa position au repos. Une fois en mouvement, aucune force externe n'est appliquée au système. La masse oscille librement et sans aucune contrainte. Dans ces conditions, la fréquence de la vibration du système est définie comme étant sa fréquence naturelle fn.
La fréquence naturelle d'un système "masse-ressort" diminue avec l'accroissement de la masse m et augmente avec la constante de rappel k du ressort. La constante de rappel caractérise la rigidité du ressort. La masse se déplacera plus au moins vite selon que le ressort est plus ou moins rigide. Vous pouvez observer à la figure suivante l'effet que produit l'addition d'une masse sur la période d'oscillation du système.
Relation entre fn, m et k :
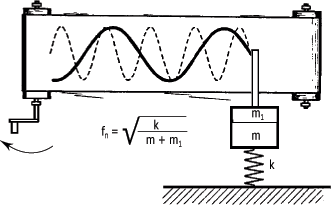
Un mécanisme simple comme une masse, un objet ou un composant unique qui oscille dans une direction donnée possède une seule fréquence naturelle. Un mécanisme complexe comme une voiture, une machine industrielle ou encore le corps humain en possède plusieurs.
Pouvez-vous imaginer un système mécanique qui vibre naturellement sans que jamais l'amplitude du phénomène ne diminue avec le temps, c'est-à-dire que le mouvement se répète de façon périodique sans perte d'énergie ? Oui ? Vous avez beaucoup d'imagination ! Poursuivez quand même votre apprentissage, le mouvement perpétuel n'a pas encore été découvert…
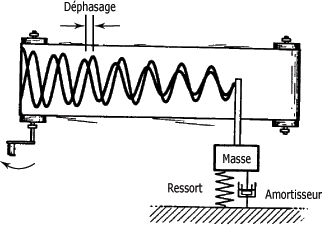
Pour compenser la perte d'énergie due aux forces de frottement, on peut appliquer une force extérieure et on obtient alors une vibration forcée.
Si une force sinusoïdale externe est appliquée au système "masse-ressort-amortisseur", le système suit le mouvement de la force, c'est-à-dire que la fréquence du système fS est identique à celle de la force externe fF.
Il en résulte que la période du système TS est aussi égale à celle de la force externe TF. Par contre, l'amplitude peut différer et un déphasage peut apparaître, comme vous pouvez le voir à la figure suivante.
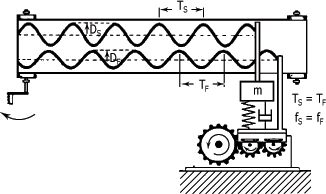
Si la fréquence d'une force externe est augmentée, la fréquence du "système masse-ressort-amortisseur" augmente de la même valeur mais, comme vous l'avez vu précédemment, l'amplitude et la phase peuvent être différentes.
D'après vous, quel phénomène va se produire si la fréquence de la force externe appliquée au système continue d'augmenter jusqu'à coïncider avec la fréquence naturelle du système "masse-ressort-amortisseur" ?
Un indice peut-être ? Avez-vous déjà voyagé à l'intérieur d'une automobile qui, lorsqu'elle atteignait une certaine vitesse, se mettait soudainement à vibrer. Si votre réponse est oui, vous avez alors été en présence du phénomène de résonance.
La figure suivante vous montre que l'amplitude d'une vibration forcée DS atteint un maximum pour une certaine fréquence de la force appliquée au système "masse-ressort-amortisseur". Cette fréquence est appelée fréquence de résonance. S'il n'y pas d'amortissement, l'amplitude tend à l'infini à la fréquence de résonance fO (trait pointillé).
Phénomène de résonance :
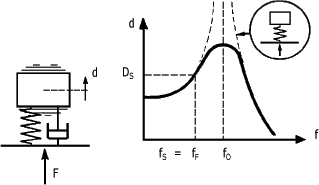
Sur le plan physique, la très grande amplitude des oscillations à la fréquence de résonance s'explique par le fait que le système reçoit de l'énergie dans les conditions les plus favorables. En effet, à la résonance, la force appliquée et la vibration sont en phase ; la puissance transmise au système est maximale.
La résonance joue un très grand rôle dans les phénomènes les plus variés. Elle produit un effet utile dans certains cas - résonance acoustique d'une salle - et un effet nuisible dans d'autres comme celui produit par un déséquilibre.
Un déséquilibre dans une machine est la cause de l'apparition d'une force périodique agissant sur les paliers. La période de cette force peut se trouver égale à la période d'oscillation libre du palier ou, par exemple, à la période d'oscillation du rotor (pompe, ventilateur, etc.). Il y a donc résonance et les oscillations forcées peuvent devenir si fortes qu'elles détruisent les paliers et provoquent une défaillance.
Les constructeurs de machines industrielles et les constructeurs d'automobiles prennent très au sérieux le phénomène de résonance. Des sommes considérables sont investies par les constructeurs d'automobiles afin d'éliminer la résonance dans le seul but d'accroître le confort de leurs véhicules. Les constructeurs de machines industrielles s'assurent d'éviter les risques de résonance en régime normal de fonctionnement par une conception appropriée de leurs machines.
Le mouvement vibratoire d'une machine ou d'une partie de machine est rarement un mouvement périodique simple comme celui décrivant le mouvement d'une masse suspendue à un ressort (déjà étudié), d'un pendule ou encore d'un diapason.
Par contre, il est possible de démontrer mathématiquement (théorème de Fourier) que tout mouvement périodique de période T, aussi complexe soit-il, peut être décomposé en une somme de mouvements sinusoïdaux de périodes égales à T, T/2, T/3, T/4, etc., c'est-à-dire de fréquences f = 1/T, 2f, 3f, 4f, etc.
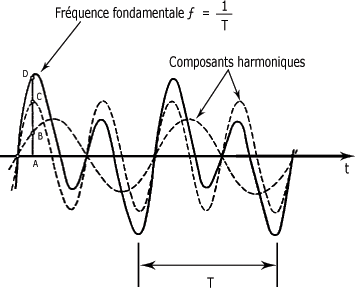
La fréquence f la plus basse est appelée fréquence fondamentale. La vibration de fréquence fondamentale f est appelée premier harmonique (on dit aussi harmonique d'ordre 1), alors que les vibrations de fréquences 2f, 3f, 4f, etc., sont appelées composantes harmoniques ou harmoniques supérieurs (deuxième, troisième, quatrième, etc.).
La figure suivante vous montre (en trait plein) un mouvement périodique. Il se répète de façon régulière en fonction du temps. Il est en fait constitué de deux composantes harmoniques - en traits pointillés - additionnées l'une à l'autre. Vous pouvez constater que le niveau du signal complexe au point A, représenté par le segment AD, correspond à la somme des niveaux représentés par les segments AB et AC.
Mouvement sinusoïdal harmonique et fondamental :
L'analyse en fréquence est une technique fondamentale dans la mesure des vibrations et le diagnostic des défauts.
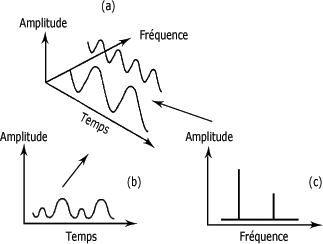
Un graphique d'amplitude en fonction de la fréquence facilite beaucoup l'identification des différentes composantes constituant un signal de vibration périodique. Chacune des composantes apparaît comme une ligne verticale dont la hauteur correspond à leur amplitude respective. La position de chaque ligne en indique la fréquence. Cette représentation est appelée spectre de fréquence (figure (c) ci-après).
La relation "temps-fréquence" vous
est montrée de manière graphique à
la
figure suivante. Remarquez
que le signal ne possède que deux composantes harmoniques
(partie (a) de la
figure). Malgré tout, il vous
sera presque impossible à partir de la seule
représentation du signal dans le domaine du temps (partie
(b) de la figure)
de décomposer le signal en ses deux
composantes originales.
C'est
pourquoi la représentation du signal dans le domaine des
fréquences (partie (c) de la
figure)
est la plus couramment utilisée en analyse des
vibrations.
Relation "temps-fréquence" :
Quand vous procédez à l'analyse des vibrations sur les machines tournantes, vous avez rarement affaire à un signal aussi simple que celui de la figure avec seulement deux composantes. En pratique, on trouve un certain nombre de composantes fréquentielles prédominantes qui sont rattachées aux mouvements fondamentaux de la machine.
Vous pouvez voir à la figure suivante l'exemple (simplifié) d'un spectre de fréquences représentant clairement les sources de vibration que sont :
• le déséquilibre (associé au mouvement d'un arbre en rotation) ;
• un défaut de roulement (associé au mouvement des billes ou rouleaux) ;
• une fréquence d'engrènement (associée au mouvement des roues dentées).
Vibration d'une machine en fonction du temps et de la fréquence :
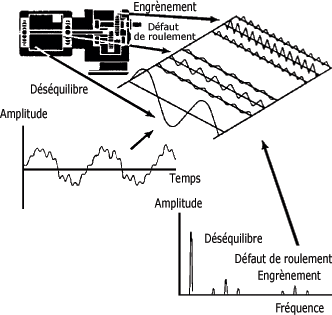
Chacune des lignes prédominantes du spectre de fréquence correspond à une composante harmonique du signal vibratoire. L'addition dans le domaine du temps de toutes ces composantes harmoniques représente le signal vibratoire tel que mesuré sur la machine.
Le spectre de fréquence caractérise donc tout à fait la vibration d'une machine, aucune information n'est perdue en convertissant le signal dans le domaine des fréquences.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !







