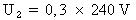Transformateurs monophasés (1)

De nombreux appareils sont conçu pour fonctionner en très basse tension :

• soit pour des raisons de sécurité,
• soit pour pouvoir être alimentés à partir de piles ou de batteries,
• soit encore parce qu'ils utilisent des composants électroniques.

Pour pouvoir les brancher sur le secteur, il faut déjà abaisser la tension au niveau adéquat. Pour les petites puissances, on utilise un transformateur monophasé.

Dans cette étude, nous ferons un rappel sur le principe de fonctionnement, la formule de Boucherot qui permet de déterminer la valeur de la f.é.m. induite et le rapport de transformation.

Vous verrez ensuite :

• leur constitution,
• puis les transformateurs triphasés.

Un transformateur est constitué de deux enroulements réalisés autour d'un circuit magnétique, comme le montre la figure suivante.

Schéma de principe d'un transformateur :

Le premier enroulement, constitué de N₁ spires, est appelé le primaire du transformateur. Si on l'alimente par une source de tension alternative U₁, il se crée un flux ø variable. Si la tension est sinusoïdale, comme c'est le cas généralement, le flux est également sinusoïdal.

Le second enroulement, constitué de N₂ spires, est appelé le secondaire du transformateur.

On sait que si un conducteur, une spire ou une bobine sont placés dans un champ magnétique variable, ils seront le siège de forces électromotrices (f.é.m.) induites.

C'est le cas de l'enroulement secondaire qui est traversé par le flux variable produit par le primaire et canalisé par le circuit magnétique. Le secondaire du transformateur sera donc le siège d'une f.é.m. induite U₂ sinusoïdale.

C'est la variation du flux qui est à l'origine de la f.é.m. induite. Si la tension du primaire est sinusoïdale, le flux l'est également et ses variations sont telles que la f.é.m. est également sinusoïdale. Mais si la tension du primaire est continue, le flux est constant et n'engendre pas de f.é.m. induite. Si U₁ est une tension continue, alors U₂ = 0 V.

Formule de Boucherot :

La formule de Boucherot nous permet de calculer la valeur efficace de la f.é.m.

E induite dans un enroulement constitué de N spires et soumis à un champ magnétique variable et sinusoïdale de valeur maximale B et de fréquence f :

.

Avec : S est la section en m² du circuit magnétique ;

B en Teslas (T).

La f.é.m. induite est proportionnelle à l'intensité du champ magnétique, au nombre de spires et à la fréquence.

Le problème qui suit vous permettra d'appliquer la formule de Boucherot.

Problème :

Calculer à l'aide de la formule de Boucherot la f.é.m. induite dans un enroulement de 80 spires si le champ magnétique est sinusoïdal, de valeur maximale 2 Teslas et de fréquence 50 Hz. La section est de 10 cm².

Solution :

Appliquons la formule de Boucherot :

.

Avec :

B = 2 T ;
S = 10 cm² = 0,001 m² ;
N = 80 spires ;
f = 50 Hz.

D'où :

.

E = 35,5 V.

La f.é.m. induite dans l'enroulement est de 35,5 V.

Le rapport de transformation, que l'on note m, est le rapport de la tension du secondaire sur celle du primaire.

Si l'on néglige les chutes de tension, il s'écrit :

.

Il est indépendant de la charge et puisque la formule de Boucherot vous a montré que la f.é.m. est proportionnelle au nombre de spires, on peut dire également que le rapport de transformation est aussi  celui du nombre de spires de l'enroulement secondaire sur celui de l'enroulement primaire.

.

Les transformateurs ont un très bon rendement, proche de l'unité, en particulier ceux de grande puissance. Cela signifie que la puissance absorbée est pratiquement égale à la puissance fournie par le transformateur à la charge.

Si P₁ est la puissance active absorbée au primaire et P₂ la puissance active fournie par le secondaire, on peut écrire :

P₁ = P₂.

Il en sera de même pour la puissance réactive :

Q₁ = Q₂.

Et par conséquent nous avons aussi égalité des puissances apparentes :

S₁ = S₂ soit U₁ I₁ = U₂ I₂.

I₁ est le courant de l'enroulement primaire et I₂ celui du secondaire.

Puisque :

U₁ I₁ = U₂ I₂  et que :

.

Alors nous avons :

.

Problème :

Calculer le rapport de transformation d'un transformateur ayant 1 500 spires au primaire et 450 spires au secondaire. Calculer la tension et le courant du secondaire si le primaire est alimenté en 240 V et absorbe 1,3 A.

Solution :

1-Calcul du rapport de transformation :

.

Avec : N₂ = 450 spires et N₁ = 1 500 spires.

.

Le rapport de transformation du transformateur est égal à 0,3.

2-Calcul de la tension et du courant du secondaire :

.

D'où on tire les relations :

U₂ = 72 V.

Le courant secondaire vaut :

 ;

I₂ = 4,33 A.