Rappel des caractéristiques électriques des circuits série (1)
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Vous avez déjà étudié les caractéristiques électriques des circuits série. Voici néanmoins un court rappel sur le comportement des principaux paramètres électriques dans ce type de circuit.
• Résistance
Dans un circuit série, la résistance équivalente (Req) est égale à la somme de chacune des résistances formant le circuit :
Req = R1 + R2 + R3… + Rn
• Courant
Dans un circuit série, le courant est identique en tous points du circuit, car il n'existe qu'un seul chemin pour la circulation des électrons :
It = I1 = I2 = I3… = In
Pour cette raison, dans les circuits série, on ne parle pas de It, I1, etc. mais tout simplement de I.
• Tension
Dans un circuit série, la somme des chutes de tension est égale à la tension de la source :
U = V1 + V2 + V3… + Vn
La première loi de Kirchhoff, en relation avec les tensions, démontre cette affirmation.
• Maille
Une maille constitue un chemin fermé dans un circuit électrique.
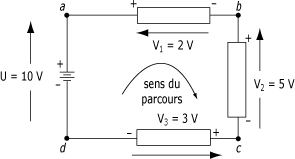
Sur la figure présentée plus loin, le chemin parcouru en partant de a, en suivant b, c, d et retour en a constitue une maille. En fait ce circuit est constitué d'une seule maille, mais en réalité les circuits électriques sont constitués d'un grand nombre de mailles.
On choisit un point de départ et un sens de parcours arbitraire pour la maille. La loi des mailles ou 1ère loi de Kirchhoff dit que la somme algébrique des tensions rencontrées en décrivant la maille dans le sens choisi est nulle.
Convention : si la flèche d'une tension rencontrée est dans le sens du parcours, la tension est positive, sinon elle est négative.
La figure suivante montre cette situation. Si l'on complète la maille à partir du point a et que l'on se déplace dans le sens horaire, on obtient les tensions suivantes :
- V1 - V2 - V3 + U = 0 V
- 2 V - 5 V - 3 V + 10 V = 0 V
Première loi de Kirchhoff :
Cette loi permet de calculer rapidement la tension aux bornes d'une résistance d'un circuit série. Voici un exemple illustrant la manière de procéder.
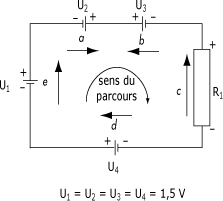
Problème: quelle sera la tension (V1) aux bornes de la résistance du circuit montré à la figure ci-dessous ?
Application de la première loi de Kirchhoff :
Appliquons la boucle des tensions, conformément à la première loi de Kirchhoff :
U2 - U3 - V1 + U4 + U1 = 0 ;
V1 = + U2 + U4 + U1 - U3 ;
V1 = + 1,5 V + 1,5 V + 1,5 V - 1,5 V ;
V1 = 3 V.

On obtiendrait le même résultat en partant de n'importe quel point du circuit.
La tension aux bornes de la résistance du circuit est donc égale à 3 V.
Comme vous l'avez vu précédemment, la puissance dissipée par la résistance provient de la source.
Dans un circuit série, la puissance totale fournie par la source est égale à la somme des puissances dissipées par chacune des résistances :
Pt = P1 + P2 + P3… + Pn.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !







