Modulation d'une tension sinusoïdale
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Un grand nombre de signaux sonores peuvent être transmis simultanément par une onde électromagnétique de très grande fréquence, appelée onde porteuse.
Pour cela, cette onde porteuse doit être modulée par ces signaux sonores.
En quoi cela consiste-t-il ?
Pourquoi moduler la porteuse ?
Comment recevoir l’un de ces signaux sans que les autres n’interfèrent sur la réception ?
Moduler un signal, c'est modifier l'une de ses caractéristiques.
L'expression mathématique d'une tension sinusoïdale u(t), de fréquence f, d'amplitude Um et de phase à l'origine φ est :
Pour moduler u(t), on peut modifier sa fréquence, son amplitude ou sa phase.
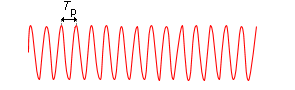
Doc. 1. Porteuse de période
Tpet de fréquence
fp.
Le signal à transporter est associé à la
tension modulante us(t) (signal
contenant l'information) :
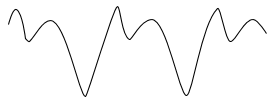
Doc. 2. Tension modulante.
L'amplitude Um de la portante a été modulée par us(t) :
L'amplitude est donc une fonction affine de us(t).
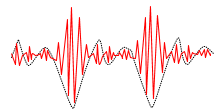
Doc. 3. Signal modulé.
Le signal modulé (doc. 3) a donc pour expression :
u(t) = Um cos(2π fp t) = [a us(t) + b] cos(2π fp t) .
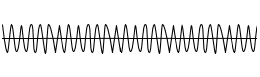
Doc. 4. Porteuse.
Le signal à transporter est associé à la tension modulante us(t) (signal contenant l'information) :
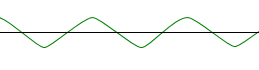
Doc. 5. Tension modulante us(t).
La fréquence de la portante a été modulée par us(t) :
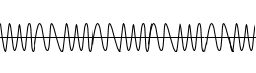
Doc. 6. Modulation de la fréquence de la porteuse.
L'information que l'on souhaite transmettre (parole, musique,
etc) est constituée de signaux qui ont des
fréquences de l'ordre du
kilohertz et donc des longueurs d'onde
voisine de 100 km.
Ces basses fréquences ne sont pas adaptées à
la transmission par ondes hertziennes pour plusieurs raisons
:
• les antennes qui ont des dimensions du
même ordre de grandeur que la longueur d'onde du signal
qu'elles émettent seraient immenses ;
• une propagation dans l'air sur de grandes distances
nécessite des fréquences plus
élevées (MHz), par pallier à
l’atténuation du signal ;
• les récepteurs ne pourraient pas séparer les
différentes émissions reçues et il y aurait
brouillage de l'information et la nécessité de
canaux de transmission.
L’une des raisons de la modulation des ondes hertziennes
est de pouvoir transporter plusieurs signaux
simultanément.
Cependant, comment réceptionner ces signaux sans
qu’ils n’interfèrent entre eux ?
Il faut utiliser un filtre qui permet de ne laisser passer que les tensions associées aux ondes que nous voulons capter (c’est ce que nous faisons lorsque nous sélectionnons une station radio).
Pour cela, on utilise un dipôle LC
parallèle qui est relié à
l’antenne. Expérimentalement, il est facile de
montrer que ce dipôle atténue fortement certaines
tensions qui le traversent alors qu’il en laisse passer
d’autres sans les atténuer. Il agit ainsi
comme un filtre et ne laisse passer que les tensions dont les
fréquences appartiennent à sa bande passante
Δf.
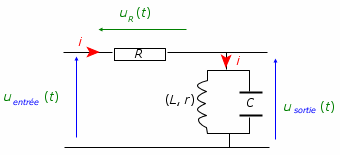
Doc. 7. Dipôle LC parallèle agissant comme un filtre.
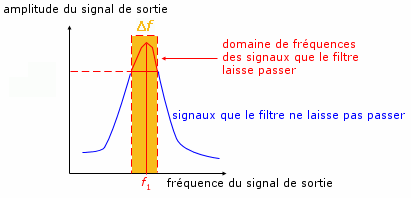
Doc. 8. Courbe obtenue avec un dipôle LC en parallèle : la fréquence
des tensions que laisse passer le filtre sont dans la bande passante Δf.
La fréquence de la tension d'entrée permettant d'obtenir un maximum d'amplitude pour la tension de sortie est égale la fréquence propre d'oscillation fr du dipôle LC.
La capacité C du condensateur (ou l'inductance L de la bobine) est réglable et permet de choisir la valeur de fr , c'est-à-dire le domaine de fréquences des tensions que le filtre laissera passer :
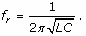
Remarque : Le filtre agit comme un circuit bouchon pour l'intensité, c'est-à-dire que pour les fréquences appartenant à la bande passante Δf, l'intensité i du courant est minimale, et par conséquent, la tension ur(t) est minimale.
• Moduler une tension sinusosîdale, c'est modifier l'une de ses caractéristiques : son amplitude, sa fréquence, sa phase à l'origine des dates.
• Moduler l'amplitude d'une tension u(t), c'est rendre l'amplitude de la porteuse, Um, fonction affine de la tension modulante us(t) :
• Les voies hertziennes permettent la transmission
simultanée d'un grand nombre de signaux sonores.
Il faut utiliser un dipôle LC pour filtrer
certaines tensions associées à ces signaux et
n'entendre que les sons souhaités. Le filtre
sélectionne les canaux de transmission.
• La fréquence de résonance qui permet
d'accorder le filtre, c'est-à-dire d'obtenir une tension
de sortie d'amplitude maximale est :
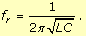

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !







