Méthode d'équilibrage (1)
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Le principe de l'équilibrage "in situ" consiste à procéder à des déséquilibrages contrôlées (habituellement temporaires) de la masse du rotor au moyen de masses d'essai. Cette procédure vous sera d'abord présentée dans ses grandes lignes.
Vous apprendrez ensuite à choisir une masse d'essai convenable, à vérifier la validité des mesures de vibration, à tracer un diagramme vectoriel pour calculer les corrections requises, à corriger le déséquilibre et, finalement, à vous familiariser avec les différentes techniques de corrections de masse sur le rotor.
Pour équilibrer un rotor, vous devez placer une masse de correction d'une certaine grosseur à un endroit où elle annule le balourd du rotor, c'est-à-dire en un point qui lui est diamétralement opposé. Pour ce faire, il vous faut déterminer la valeur et la position de la masse de correction.
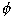 0)
0)
La procédure d'équilibrage "in situ" consiste d'abord à mesurer la vibration causée par le déséquilibre du rotor qui, comme vous le savez maintenant, apparaît toujours dans le spectre de vibrations à la fréquence de rotation de l'arbre (figure suivante).
Déséquilibre dans le spectre de vibrations :
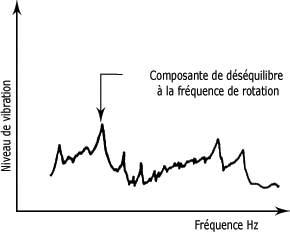
La mesure de l'amplitude vibratoire, proportionnelle à la force produite par le balourd, requiert l'emploi d'un accéléromètre monté sur le palier du roulement. La mesure de la phase, essentielle pour localiser la "partie lourde" dans le rotor à équilibrer, requiert l'emploi d'un capteur tachymétrique.
Le capteur tachymétrique, monté à une distance appropriée de la surface du rotor, peut aussi bien être une sonde photo-électrique ou une lumière stroboscopique.
La figure suivante vous montre le montage de l'accéléromètre et de la sonde photo-électrique de même que celui d'une bande réfléchissante fixée sur le rotor. Le passage de la bande réfléchissante déclenche la sonde photo-électrique une fois par tour et une impulsion est envoyée à l'analyseur de vibrations.
Vous obtenez alors les deux
résultats de mesure suivants :  0, soit l'angle de phase
du signal vibratoire par rapport à l'impulsion du capteur
tachymétrique ; A0, soit la vibration
causée par le balourd, aussi appelée "amplitude
initiale".
0, soit l'angle de phase
du signal vibratoire par rapport à l'impulsion du capteur
tachymétrique ; A0, soit la vibration
causée par le balourd, aussi appelée "amplitude
initiale".
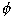 1)
1)
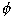 0,
vous devez placer une masse d'essai connue sur le rotor. La masse
d'essai a pour effet de modifier l'amplitude et l'angle de phase
de la vibration. Vous obtenez alors les mesures suivantes :
A1 et
0,
vous devez placer une masse d'essai connue sur le rotor. La masse
d'essai a pour effet de modifier l'amplitude et l'angle de phase
de la vibration. Vous obtenez alors les mesures suivantes :
A1 et
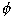 1,
soit l'amplitude et la phase de la vibration avec la masse
d'essai.
1,
soit l'amplitude et la phase de la vibration avec la masse
d'essai.
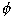 c)
c)
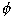 c.
c.
Il ne vous reste plus qu'à poser la masse de correction à l'endroit approprié sur le rotor et à mesurer de nouveau l'amplitude et l'angle de phase de la vibration. Si la vibration résiduelle ne se trouve pas en deçà d'un seuil acceptable, vous devrez reprendre le cycle d'équilibrage.
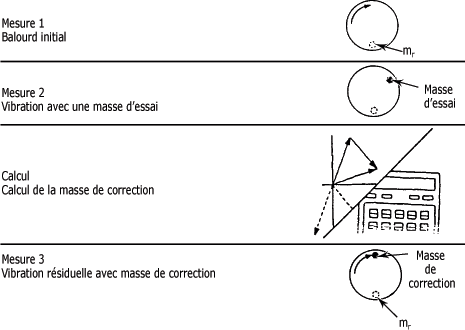
Vous trouverez à la figure suivante un résumé des principales étapes de la procédure d'équilibrage sur un plan. La masse initiale de déséquilibre y est représentée par la valeur mr.
Procédure d'équilibrage :
Les calculs de correction du déséquilibre sont basés sur les changements que produit la masse d'essai sur l'état initial du rotor. Il est donc important de choisir une masse qui permette d'obtenir de bons résultats. Sélectionnez une masse trop petite et vous ne noterez aucun changement d'amplitude ou de phase ; sélectionnez une masse trop grande et vous risquez d'endommager la machine.
Vous allez apprendre que la valeur du balourd résiduel admissible Uadm peut servir à donner une valeur appropriée de la masse d'essai.
Le balourd résiduel admissible est
obtenu en multipliant le balourd spécifique par la masse
du rotor, soit Uadm = eadm
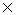 M. Vous trouvez le balourd
spécifique eadm à l'aide de
l'abaque Iso, en fonction du degré de qualité
d'équilibrage requis et de la vitesse maximale de
fonctionnement du rotor.
M. Vous trouvez le balourd
spécifique eadm à l'aide de
l'abaque Iso, en fonction du degré de qualité
d'équilibrage requis et de la vitesse maximale de
fonctionnement du rotor.
La norme Iso 1940 recommande de choisir une masse équivalente à 5 à 10 fois le balourd résiduel admissible comme masse d'essai. Vous pouvez convertir le balourd résiduel en une masse équivalente mr, appelée masse résiduelle, en le divisant par le rayon de correction rc, soit la distance entre l'axe de l'arbre et l'emplacement de la masse de correction. Sur de nombreux rotors, le rayon de correction et le rayon de pose de la masse d'essai re sont identiques. Par conséquent :

mr =
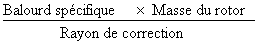
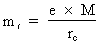
La figure suivante reprend l'exemple déjà proposé, soit celui d'un rotor classé G6,3 et dont la vitesse maximale de fonctionnement est de 50 Hz (3 000 r/min). Il a été établi précédemment, au moyen de l'abaque Iso, que le balourd résiduel spécifique pour ce rotor ne devait pas dépasser 20 g · mm/kg après équilibrage.
Si la masse du rotor M est
de 50 kg et que le rayon de pose de la masse d'essai
re est
de 100 mm, alors : mr = 20 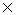 50/100 = 10 g. La masse
d'essai doit donc être comprise entre 50
et 100 g.
50/100 = 10 g. La masse
d'essai doit donc être comprise entre 50
et 100 g.
Malgré tout le soin que vous pouvez apporter à la sélection de la masse d'essai, il peut arriver que celle-ci ne donne pas des résultats acceptables pour les calculs d'équilibrage. C'est pourquoi il est très important de vérifier la validité des mesures avant de procéder aux calculs de la masse de correction.
Le tableau de la figure suivante montre les quatre possibilités susceptibles de
se produire après la pose de la masse d'essai. Le
symbole "triangle"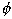 représente l'écart entre l'angle de
phase mesuré avant et après la pose de la masse
d'essai.
représente l'écart entre l'angle de
phase mesuré avant et après la pose de la masse
d'essai.
Le symbole "triangle" A représente l'écart entre l'amplitude vibratoire mesurée avant et après la pose de la masse d'essai.
Évaluation des effets de la masse d'essai :

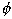 est inférieur à 25°, vous devez
augmenter la valeur de la masse d'essai ou encore déplacer
celle-ci selon que l'écart d'amplitude "triangle"A soit plus
plus petit ou plus grand que 25 %. Si l'écart de
phase "triangle"
est inférieur à 25°, vous devez
augmenter la valeur de la masse d'essai ou encore déplacer
celle-ci selon que l'écart d'amplitude "triangle"A soit plus
plus petit ou plus grand que 25 %. Si l'écart de
phase "triangle"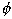 dépasse 25°, les valeurs
mesurées peuvent servir à calculer la valeur et l'angle
de la masse de correction.
dépasse 25°, les valeurs
mesurées peuvent servir à calculer la valeur et l'angle
de la masse de correction.
Valeurs mesurées :
Les mesures suivantes sont effectuées :
- A0 et
0, soit l'amplitude et l'angle de phase du balourd initial ;
- A1 et
1, soit l'amplitude et l'angle de phase du balourd avec la masse d'essai.
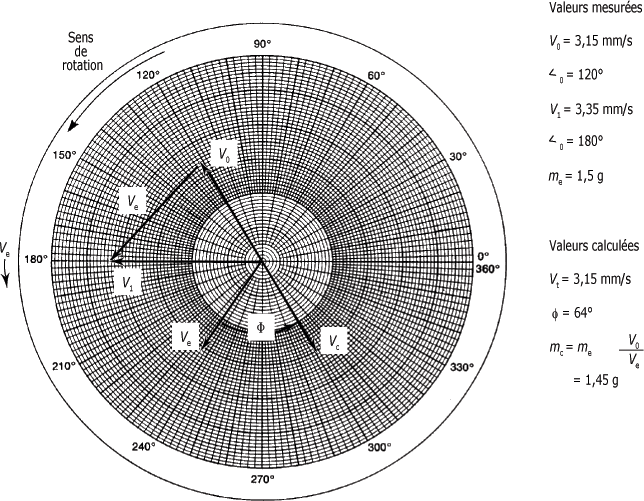
Vous pouvez déterminer les valeurs de la masse et de l'angle de correction en représentant d'abord les mesures sous la forme de vecteur. Le diagramme vectoriel des valeurs mesures, montré à la figure 4.22, est construit selon la procédure suivante :
1. Tracer un vecteur
V0
représentant le balourd initial. La longueur de
V0 est
égale à l'amplitude A0 et sa direction est
donnée par l'angle de phase 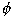 0 (partie
a de la
figure ci-dessous).
0 (partie
a de la
figure ci-dessous).
2. Tracer un autre
vecteur V1 représentant le
balourd (amplitude A1 et angle de phase
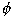 1) mesuré avec la
masse d'essai (partie b
de la
figure ci-dessous).
1) mesuré avec la
masse d'essai (partie b
de la
figure ci-dessous).
3. Tracer un vecteur de la pointe de V0 à celle de V1 en prenant soin de lui donner la direction indiquée à la partie c de la figure ci-dessous. Le nouveau vecteur Ve représente la contribution de la masse d'essai seule sur la nouvelle condition de déséquilibre du rotor.
Cette information va vous permettre de localiser avec précision la position de la masse de déséquilibre à l'origine du balourd initial et de calculer la masse de correction nécessaire pour l'éliminer sinon pour le réduire à une valeur acceptable.
Diagramme vectoriel : valeurs mesurées :
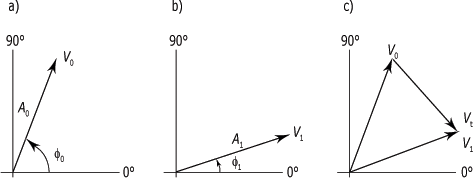
Les valeurs mesurées étant représentées sur le diagramme vectoriel, les calculs, montrés à la figure ci-dessous, se font comme suit :
1. Tracer un nouveau vecteur Ve parallèle au vecteur Ve existant, suivant la même direction mais à partir de l'origine (partie d de la figure ci-dessous).
2. Reproduire le vecteur V0 de l'autre côté de l'origine mais dans une direction opposée. Le nouveau vecteur appelé Vc représente la position et la valeur du balourd nécessaires pour annuler le balourd initial V0 et ainsi équilibrer le rotor (partie e de la figure ci-dessous).
Diagramme vectoriel : valeurs calculées :
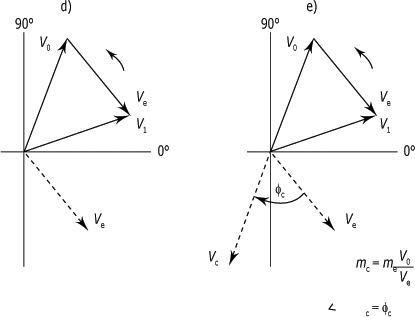
Finalement, la valeur et la position de la masse de correction sont déterminées de la façon suivante :
1. Imaginez
maintenant que vous fassiez pivoter le vecteur en
pointillé Ve jusqu'à ce qu'il se
confonde avec le vecteur Vc. L'angle 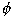 c représente
l'angle de rotation nécessaire. Il correspond aussi à
l'angle de correction
c représente
l'angle de rotation nécessaire. Il correspond aussi à
l'angle de correction 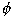 c dont le sens est
donné suivant la rotation de l'arbre ; positif dans
le sens de rotation ; négatif dans le sens
contraire.
c dont le sens est
donné suivant la rotation de l'arbre ; positif dans
le sens de rotation ; négatif dans le sens
contraire.
2. La prochaine
étape consiste à augmenter ou à diminuer la
longueur de Ve jusqu'à égaler
celle de Vc. Pour ce faire, on suppose
que l'amplitude vibratoire est proportionnelle au balourd. Vous
pouvez ainsi établir que me/Ve = mc/Vc = mc/V0,
ce qui vous permet de calculer la valeur de lamasse de
correction mc, soit mc = me
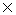 V0/Ve.
V0/Ve.
Dans la pratique, le diagramme et les calculs vectoriels sont tracés sur une feuille de papier graphique polaire à l'aide d'une règle et d'un rapporteur. La figure suivante vous en montre un exemple.
Diagramme vectoriel, exemple pratique :

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !







