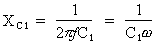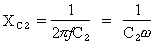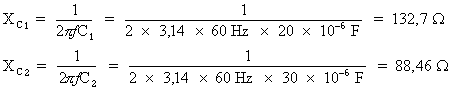Les caractéristiques du condensateur
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Comme les bobines, les condensateurs dans les circuits électriques et électroniques peuvent aussi être raccordés:
- soit en série,
- soit en parallèle.
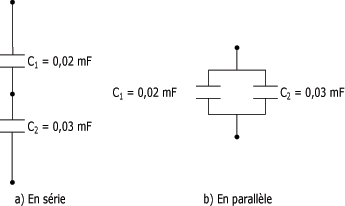
La capacité équivalente (Céq) pour chacun des types de raccordements présentés ci-dessus peut être calculée à l'aide des formules suivantes :
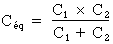 .
.
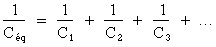
Céq = C1 + C2 + C3 + …

Pour appliquer correctement ces formules, il est nécessaire d'utiliser pour tous les condensateurs le même niveau d'unité de mesure, soit pF (picofarad ou 10-12 F), µF (microfarad ou 10-6 F).
Exemple de l'application
de ces formules :
Sachant que la capacité
de C1 est
égale à 20 µF et la capacité de
C2 est
égale à 30 µF, calculez la capacité équivalente, en
microfarads (µF), pour un raccordement en série et en
parallèle.
• Condensateurs C1 et C2 raccordés en série.
Formule pour calculer la capacité équivalente :
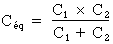 . Où :
C1 = 20 µF
et C2 = 30 µF.
Donc :
. Où :
C1 = 20 µF
et C2 = 30 µF.
Donc : 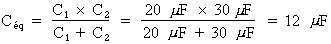 . La capacité
équivalente pour les condensateurs raccordés en
série est égale à 12 µF.
• Condensateurs C1 et C2 raccordés en
parallèle : Formule pour
calculer la capacité équivalente :
Céq = C1
+ C2.
Où : C1 = 20 µF
et C2 = 30 µF.
Donc : Céq = C1
+ C2 = 20 µF
+ 30 µF = 50 µF.
La capacité équivalente pour
les condensateurs raccordés en parallèle est égale
à 50 µF.
. La capacité
équivalente pour les condensateurs raccordés en
série est égale à 12 µF.
• Condensateurs C1 et C2 raccordés en
parallèle : Formule pour
calculer la capacité équivalente :
Céq = C1
+ C2.
Où : C1 = 20 µF
et C2 = 30 µF.
Donc : Céq = C1
+ C2 = 20 µF
+ 30 µF = 50 µF.
La capacité équivalente pour
les condensateurs raccordés en parallèle est égale
à 50 µF.
La capacité équivalente des condensateurs raccordés en série ou en parallèle est utilisée pour calculer la réactance capacitive totale (XC).
On utilise alors la formule
suivante : 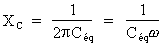 .
.
La réactance capacitive totale (XC) peut être également déterminée à partir de la réactance capacitive de chacun des condensateurs C1 et C2.
Les formules suivantes sont alors employées :
• Circuit en
série : XC = XC1 + XC2.
Où : XC :
réactance capacitive totale en ohms
XC1 : réactance
capacitive du condensateur C1 en ohms et calculée
grâce à la formule : 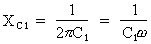
XC2 : réactance
capacitive du condensateur C2 en ohms et calculée
grâce à la formule : 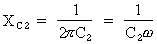
•
Circuit en parallèle :
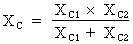
Où :
XC : réactance capacitive totale en ohms
XC1 : réactance capacitive du condensateur C1 en ohms et calculée grâce à la formule :
XC2 : réactance capacitive du condensateur C2 en ohms et calculée grâce à la formule :
Exemple de
l'application de ces formules
:
Sachant que
la fréquence du circuit est de 60 Hz,
calculez la réactance capacitive
totale, en ohms, pour chacun des circuits de la figure 2.12 à partir de :
a) la capacité équivalente ;
b) la réactance capacitive de chacun des condensateurs C1 et C2.
Solutions :
a) Réactance capacitive totale calculée à partir de la capacité équivalente
- Condensateurs raccordés en
série :
Formule pour
calculer la réactance capacitive totale :
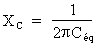
Où : Pi = 3,14, f = 60 Hz, Céq = 12 µF
(calculée précédemment).
Donc : 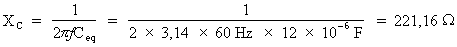
La réactance capacitive totale pour les condensateurs raccordés en série est égale à 221,16 Ohms.
- Condensateurs raccordés en
parallèle :
Formule
pour calculer la réactance capacitive totale :
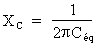
Où : Pi = 3,14, f = 60 Hz, Céq = 50 µF (calculée précédemment).
Donc : 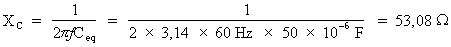 .
.
La réactance capacitive total pour les condensateurs raccordés en parallèle est égale à 53,08 Ohms.
b) La réactance capacitive totale calculée à partir de la réactance capacitive de chacun des condensateurs
1e
étape
Calcul de la
réactance capacitive de chacun des
condensateurs :
2e étape
Calcul de la réactance capacitive
totale
- Condensateurs
raccordés en série :
Formule pour calculer la réactance capacitive totale : XC = XC1 + XC2
Où : XC1 = 132,7 Ohms et XC2 = 88,46 Ohms.
Donc : XC = XC1 + XC2 + 132,7 Ohms+ 88,46 Ohms = 221,16 Ohms
La réactance capacitive totale pour les condensateurs raccordés en série est égale à 221,16 Ohms.
- Condensateurs raccordés en
parallèle :
Formule
pour calculer la réactance capacitive totale :
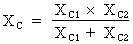
Où : XC1 = 132,7 Ohms et XC2 = 88,46 Ohms.
Donc :
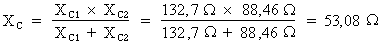
La réactance capacitive totale pour les condensateurs raccordés en parallèle est égale à 53,08 Ohms.
Analyse des résultats:
Cet exemple montre que la réactance capacitive totale est la même pour chaque type de raccordement,que le calcul soit fait à partir:
- de la capacité équivalente
- ou de la réactance capacitive de chacun des condensateurs.
Le condensateur provoque aussi un
déphasage entre le courant et la tension à ses
bornes.
Contrairement
à la bobine qui s'oppose
à la variation du courant, le condensateur s'oppose
à la variation de la tension.La
tension à ses bornes est toujours en retard
de 90° (ou 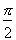 radians) par rapport au courant, comme le
montre la
figure ci-dessous.
radians) par rapport au courant, comme le
montre la
figure ci-dessous.
Illustration animée : Déphasage entre la tension et le courant dans un condensateur.

Un bon moyen pour se rappeler la relation
de phase entre la tension et le courant d'un condensateur est de
mémoriser l'acronyme "ICE".
Dans cette abréviation, la lettre
E, qui représente la tension, est
précédée par la lettre I, qui symbolise le
courant, puisque le courant est toujours en avance par
rapport à la tension.
Entre ces deux lettres apparaît le
condensateur, désigné par la lettre C, pour
capacité.
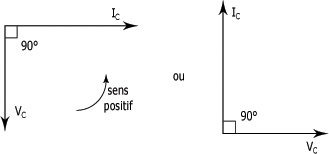
Le déphasage dans un condensateur peut aussi être représenté par un diagramme de Fresnel. Dans ce diagramme, montré à la figure 2.16, le vecteur de tension (VC) est décalé, dans le sens horaire, de 90° par rapport au vecteur de courant (IC) pour représenter le retard de phase de 90° de la tension par rapport au courant.
Diagramme de Fresnel de la tension et du courant dans un condensateur :
Aucun courant ne peut circuler à travers les plaques d'un condensateur, un matériau isolant les séparant, celui-ci ne consomme aucune énergie.
Toutefois, le condensateur doit acquérir de la source une certaine quantité d'énergie pour se charger, même si cette quantité d'énergie est restituée à la source lors du déchargement du condensateur. Cette quantité d'énergie représente la puissance réactive.
La puissance réactive d'un
condensateur, symbolisée par QC, peut être
déterminée par le produit du courant et de la tension,
comme l'exprime la formule suivante : 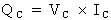 .
.
Où :
QC : puissance
réactive d'un condensateur en VARS
VC : tension aux
bornes du condensateur en volts (V)
IC : courant du
condensateur en ampères (A)
Il est important de noter que
l'unité de mesure de la puissance réactive d'un
condensateur est la même que celle de la puissance
réactive d'une bobine, soit le VAR.
Comme il a déjà été
démontré, la loi d'Ohm permet d'exprimer la relation
entre la tension et le courant de la façon
suivante :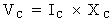 et
et
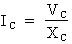 .
.
Ainsi la puissance réactive associée à
un condensateur peut être déterminée grâce
aux formules suivantes : 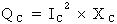 ou
ou 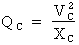 .
.
Où :
QC : puissance réactive d'un condensateur en VARS.
IC: courant du condensateur en ampères (A).
XC : réactance capacitive en ohms.
En résumé sur le condensateur :
Après avoir étudié le contenu de cette étude, vous devriez retenir plus particulièrement les points suivants :
• Le condensateur est construit à partir de deux plaques conductrices placées parallèlement, face à face et séparées par un matériau non conducteur (isolant).
• Chaque condensateur est caractérisé par sa capacité, symbolisée par C et exprimée en farads (F).
• La réactance capacitive est un genre de résistance que présente le condensateur pour s'opposer au passage d'un courant alternatif.
• Deux condensateurs raccordés en série ou en parallèle peuvent être considérés comme un seul condensateur possédant une capacité équivalente. Le calcul de la réactance capacitive totale des condensateurs peut être obtenu soit à partir de la capacité équivalente, soit à partir de la réactance capacitive de chacun des condensateurs.
• Dans un condensateur, l'augmentation de la fréquence implique une diminution de la réactance capacitive et une augmentation du courant. Par contre, la diminution de la fréquence a pour effet d'augmenter la réactance capacitive et de diminuer le courant.
• Le courant est toujours en avance de phase de 90° (ou
radians) par rapport à la tension aux bornes d'un condensateur. Ce déphasage peut être représenté par un diagramme de Fresnel.
• La puissance associée à un condensateur est une puissance réactive (QC).
Ce résumé complète l'étude portant sur les principales caractéristiques des condensateurs dans un circuit à courant alternatif.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !