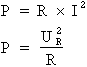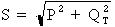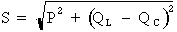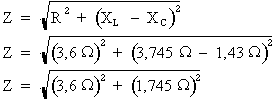Impédance circuit RLC en série (2)

L'étude sur les circuits inductifs - RL et sur les circuits capacitifs - RC vous ont montrées qu'il existe généralement dans un circuit à courant alternatif trois types de puissances :

• la puissance active,
• la puissance réactive,
• la puissance apparente.

Vous savez désormais que ces puissances dépendent des composants du circuit.

Dans un circuit RLC,

• la puissance active est celle engendrée par la résistance du circuit ;
• la puissance réactive est celle associée au condensateur et à la bobine ;
• la puissance apparente est celle fournie par la source pour combler la demande du circuit.

Par définition, la puissance active est la quantité d'énergie réellement consommée par une charge. Dans le cas d'un circuit RLC en série, la puissance active est effectivement engendrée par la résistance du circuit.

Cette puissance peut être calculée par l'une ou l'autre des formules suivantes :

Où :

P : puissance active du circuit en watts (W)
R : résistance du circuit en ohms

U_R :tension aux bornes de la résistance en volts (V)
I : courant du circuit en ampères (A)

Étant donné qu'il existe simultanément deux composants, la bobine et le condensateur, dans un circuit RLC en série, la puissance réactive totale du circuit (Q_T) correspond à la totalité des puissances réactives associées au condensateur et à la bobine.
Toutefois, à cause du déphasage entre la tension et le courant dans chacun de ces composants, la puissance réactive de la bobine est directement opposée à celle du condensateur. La figure 5.16 est une représentation vectorielle de la relation de phase entre la puissance réactive du condensateur (Q_C) et la puissance réactive de la bobine (Q_L) par rapport au courant du circuit.

Ainsi, la puissance réactive totale du circuit correspond à la somme vectorielle de Q_L et Q_C et se traduit mathématiquement par la différence entre les valeurs Q_L et Q_C : Q_T = Q_L - Q_C

Q_T : puissance réactive totale du circuit en VARS
Q_L : puissance réactive de la bobine en VARS
Q_C : puissance réactive du condensateur en VARS

Relation de phase entre la puissance réactive du condensateur et celle de la bobine :

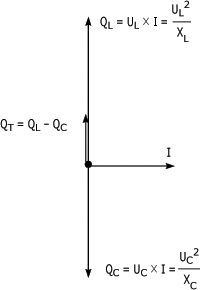
Tout comme dans le circuit inductif RL et dans le circuit capacitif RC, la puissance apparente dans un circuit RLC est déterminée par la somme vectorielle de la puissance active et de la puissance réactive totale du circuit. Elle peut être calculée grâce à la formule suivante :

Étant donné que la puissance réactive totale du circuit correspond à la différence entre les puissances Q_L et Q_C, la formule peut s'écrire comme suit :

Où :

S : puissance apparente du circuit en VA
P : puissance active du circuit en watts (W)
Q_L : puissance réactive de la bobine en VARS
Q_C : puissance réactive du condensateur en VARS

Par ailleurs, que Q_L soit plus grand ou plus petit que Q_C, cette formule est toujours valide, car le résultat de la différence entre Q_C et Q_L élevé au carré est toujours positif.
Par définition, vous savez que la puissance apparente est la puissance fournie par la source pour satisfaire la demande du circuit. Aussi, elle peut être calculée par le produit de la tension appliquée au circuit et du courant total du circuit :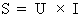

Où :

S : puissance apparente en VA
U : tension appliquée au circuit en volts (V)
I : courant total du circuit en ampères (A)

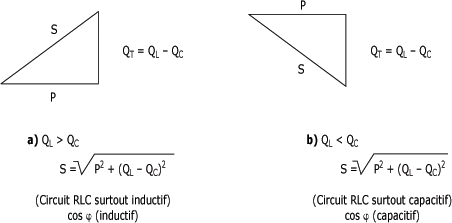
Puisque la puissance réactive totale d'un circuit RLC en série correspond à la différence entre la puissance réactive associée au condensateur et la puissance réactive associée à la bobine, la puissance réactive totale du circuit peut être selon le résultat de cette différence surtout inductive ou surtout capacitive.

La figure suivante montre les triangles des puissances correspondant à ces deux types de puissances dans un circuit RLC en série :

Comme le facteur de puissance d'un circuit est toujours déterminé par le rapport entre la puissance active et la puissance apparente du circuit 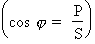 et comme le circuit RLC est surtout inductif ou surtout capacitif, il est nécessaire de bien spécifier le type de facteur de puissance.

La partie a de la figure 5.17 montre un circuit RLC qui est surtout inductif.

Dans ce circuit où Q_L > Q_C, on voit que la puissance apparente du circuit est représentée par un vecteur situé au-dessus de l'axe horizontal. Le facteur de puissance pour un tel circuit est un facteur de puissance inductif.

Par contre, dans un circuit où Q_L < Q_C, partie b de la figureci-dessus, le vecteur représentant la puissance apparente se retrouve en dessous de l'axe horizontal. Le facteur de puissance est alors un facteur de puissance capacitif.

Il a déjà été mentionné qu'un facteur de puissance trop bas 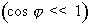 est indésirable pour un circuit électrique. En effet, dans un tel cas, la source doit effectuer un grand effort en terme de courant et de tension pour fournir au circuit une puissance apparente dont seule une partie est consommée par le circuit. Cette partie qui correspond à la puissance active.

En raison de l'effet inductif des enroulements (bobines) des moteurs, la plupart des circuits sont dans la pratique partiellement inductifs. Par conséquent, les facteurs de puissance de ces circuits sont inductifs et leur valeur plus petite que l'unité, c'est-à-dire que 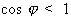. De là vient la notion de correction du facteur de puissance, qui consiste à modifier le circuit pour ramener son facteur de puissance le plus près possible de l'unité, soit .

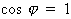Vous savez déjà qu'un circuit à courant alternatif comporte toujours trois types de puissances et que leur relation est représentée par l'équation suivante : S² = P² + Q²

Aussi, si l'on veut que le facteur de puissance soit égal à l'unité, 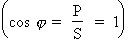, il est nécessaire que la puissance apparente soit égale à la puissance active (S = P). Autrement dit, il faut amener la puissance réactive totale du circuit à zéro.

Étant donné que la puissance réactive totale d'un circuit correspond à la différence entre la puissance réactive de la bobine et la puissance réactive du condensateur, (Q_T = Q_L - Q_C), et comme la plupart des circuits sont partiellement inductifs, il est nécessaire d'ajouter au circuit un condensateur afin de pouvoir diminuer la puissance réactive totale du circuit. Cet ajout permettra l'augmentation du facteur de puissance du circuit le plus près possible de l'unité. Voilà une des façons d'effectuer la correction du facteur de puissance.

L'exemple suivant vous montre une méthode pour corriger le facteur de puissance d'un circuit partiellement inductif en ajoutant dans le circuit un condensateur raccordé en série.

Problème :
Pour le circuit de la figure ci-dessous, calculez :

a) Le facteur de puissance du circuit avant l'ajout du condensateur.
b) La capacité du condensateur à raccorder au circuit pour obtenir un facteur de puissance égal à 0,9.
c) Le courant total du circuit après la correction du facteur de puissance.
d) Le nouveau facteur de puissance du circuit.

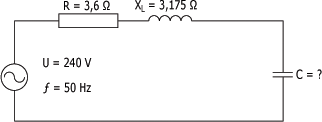
Solutions :

a) Calcul du facteur de puissance du circuit avant l'ajout du condensateur

1^e étape. Calcul de l'impédance du circuit :

Formule : 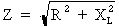où : R = 3,6 Ohms et X_L = 3,175 Ohms

Donc :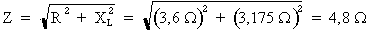

2^e étape. Calcul du courant total :

Formule : 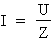où : U = 240 V et Z = 4,8 Ohms
Donc :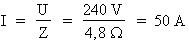

3^e étape. Calcul de la puissance active :

Formule : 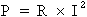 où : R = 3,6 Ohms et I = 50 A

Donc :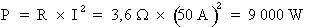

4^e étape. Calcul de la puissance apparente :

Formule : 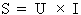 où : U = 240 V et I = 50 A

Donc :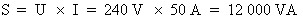

5^e étape. Calcul du facteur de puissance du circuit :

Formule : 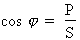 où : P = 9 000 W et S = 12 000 VA
Donc :

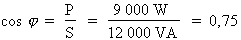
Le facteur de puissance du circuit avant l'ajout du condensateur est égal à 0,75.

b) Calcul de la capacité du condensateur à raccorder

1^e étape. Calcul de la puissance apparente :

Le but de la correction du facteur de puissance est de réduire la puissance apparente tout en satisfaisant la demande de consommation du circuit. Ainsi, on peut supposer que la puissance active du circuit est toujours la même et par conséquent établir la relation suivante :

Si : 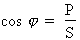 alors :

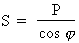
Où :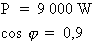
Donc :

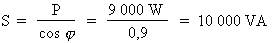
2^e étape. Calcul de la puissance réactive totale du circuit :

Si : S² = P² + Q²  alors : Q² = S² - P²

Donc : 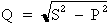 où : S = 10 000 VA et P = 9 000 W

Donc :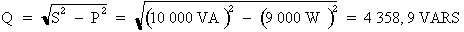

3^e étape. Calcul de la puissance réactive inductive :

Formule : 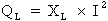 où : X_L = 3,175 OhmsΩ et I = 50 A
Donc :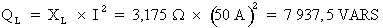

4^e étape. Calcul de la puissance réactive capacitive :

Si Q = Q_L - Q_C  alors : Q_C = Q_L - Q

Formule : Q_C = Q_L - Q où : Q_L = 7 937,5 VARS et Q = 4 358,9 VARS
Donc : Q_C = Q_L - Q = 7 937,5 VARS - 4 358,9 VARS = 3 578,6 VARS

5^e étape. Calcul de la réactance capacitive du condensateur :

Si 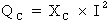 alors :

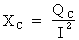
Formule :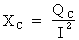  
Où : Q_C = 3 578,6 VARS et I = 50 A

Donc :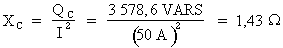

6^e étape. Calcul de la capacité du condensateur :

Si 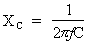 alors :

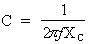
Formule :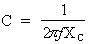  

Où : Pi = 3,14, f = 50 Hz etX_C = 1,43 Ohms

Donc :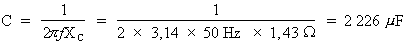

Pour obtenir un facteur de puissance de 0,9, un condensateur d'une capacité de 2 226 µF doit être ajouté au circuit.

c) Calcul du courant total du circuit après la correction du facteur de puissance

1^e étape. Calcul de l'impédance totale du circuit :

Formule : 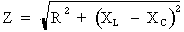 où : R = 3,6 Ohms, X_L = 3,175 Ohms et X_C = 1,43 Ohms

Donc :

2^e étape. Calcul du courant total :

Formule : 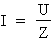 où : U = 240 V et Z = 4 Ohms
Donc :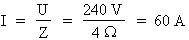

Le courant total du circuit après la correction du facteur de puissance est égal à 60 A.

d) Calcul du nouveau facteur de puissance du circuit

1^e étape. Calcul de la puissance active :

Formule : 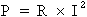 où : R = 3,6 Ohms et I = 60 A
Donc :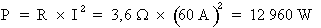

2^e étape. Calcul de la puissance apparente :

Formule : 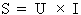 où : U = 240 V et I = 60 A
Donc :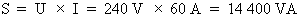

3^e étape. Calcul du facteur de puissance :

Formule :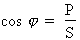

Où : P = 12 960 W et S = 14 400 VA

Donc :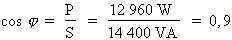

Le facteur de puissance du circuit après la correction est égal à 0,9.

Vous venez de voir un exemple dans lequel la correction du facteur de puissance d'un circuit partiellement inductif a été réalisée grâce à l'ajout d'un condensateur raccordé en série.

Vous avez pu constater qu'après la correction, le facteur de puissance du circuit se rapprochait de l'unité. Cependant, cette correction a entraîné l'augmentation du courant total du circuit, ce qui va à l'encontre de l'objectif principal de la correction du facteur de puissance, qui vise, entre autres, la diminution du courant.

A moins que ce ne soit la seule possibilité, la correction du facteur de puissance par l'ajout d'un condensateur raccordé en série au circuit est rarement utilisée.