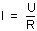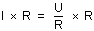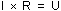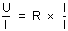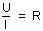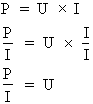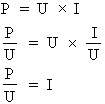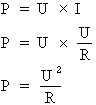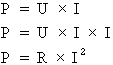Formule de la loi d'Ohm (1)

D'abord, si on augmente la résistance dans un circuit électrique, il se produit une diminution du courant. En effet, il est alors plus difficile pour les électrons de circuler, l'opposition étant plus grande. A l'inverse, si on diminue la résistance, la circulation du courant est facilitée.

D'autre part, si l'on maintient la résistance fixe, toute augmentation de la tension de la source provoquera une augmentation du courant à cause de l'augmentation de "pression" sur les électrons. Conséquemment, une diminution de la tension abaissera le courant circulant dans le circuit.

Les relations énoncées dans les paragraphes précédents permettent d'écrire la formule suivante, synthétisant la loi d'Ohm :

Courant = tension/résistance, d'où I = U/R.

Exemple d'utilisation de cette formule pour calculer la valeur du courant dans un circuit électrique :

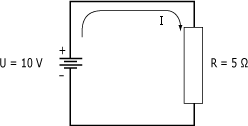
Problème : calculez la valeur du courant circulant dans le circuit simple suivant.

• Identification des données

En se reportant au circuit, on peut établir les données du problème :

U  =   10 V, R   =  5 ohms et I   =   ?

• Calcul de la valeur du courant

Il ne reste plus qu'à appliquer la formule de la loi d'Ohm pour trouver la valeur du courant :

I   =  U/R d'où I   =  10 V/5 ohms.

I   =  2 A.

Le courant circulant dans le circuit a donc une intensité de 2 A.

Pour calculer la valeur du courant lorsqu'on connaît la valeur de la tension et celle de la résistance, on applique la formule de la loi d'Ohm de façon intégrale.

Par contre, pour calculer la valeur de la tension ou celle de la résistance en utilisant cette formule, on doit isoler le paramètre recherché d'un côté de l'égalité. Pour ce faire, il faut appliquer des notions d'algèbre.

Ainsi, vous vous souviendrez que pour ne pas déséquilibrer une équation, il faut effectuer les mêmes opérations des deux côtés de l'égalité. Par conséquent :

• Si on multiplie par R les deux côtés de l'égalité, on obtient :

D'où : .

• A partir de cette dernière formule, si on divise par I les deux côtés de l'égalité, on obtient :

D'où : .

Il existe un truc pour ceux d'entre vous qui éprouvent certaines difficultés avec les transformations de formules. Reportez-vous à la figure suivante, qui illustre un cercle permettant de déterminer rapidement la relation entre les paramètres d'un circuit électrique. Il s'agit de couvrir l'unité recherchée ; celles qui restent lui sont égales.

Schéma mnémotechnique de la loi d'Ohm :

En plus du courant, de la tension et de la résistance, un quatrième paramètre est très important en électricité : la puissance électrique.

La puissance est la mesure de la quantité de travail pouvant être fournie dans un temps déterminé. La puissance est symbolisée par la lettre P et son unité de mesure est le watt (W).

Lorsqu'un courant électrique circule dans une résistance, le déplacement des électrons d'un atome à l'autre provoque un dégagement de chaleur. Sachant que la résistance ne peut elle-même produire de l'énergie, il s'ensuit que cette énergie provient de la source.

De fait, lorsqu'on fait abstraction des pertes, on peut considérer que la puissance dissipée par la résistance, sous forme de chaleur, est égale à la puissance fournie par la source.

Ainsi, plus le courant circulant dans une résistance est élevé, plus la puissance dissipée par cette résistance est grande. Comme vous l'avez vu précédemment, toute augmentation de tension aux bornes d'une résistance se traduit par une augmentation proportionnelle du courant circulant dans cette même résistance.

On peut donc conclure que la puissance électrique est directement proportionnelle à la tension et au courant : puissance = tension x courant.
D'où : P = U x I.

Exemple de calcul de la puissance d'un circuit à l'aide de cette formule :

Problème: calculez la puissance fournie par une source de tension de 100 V provoquant un courant de 2 A dans un circuit.

• Identification des données

L'énoncé du problème permet d'établir que :

U = 100 V, I = 2 A et P = ?

• Calcul de la puissance fournie par la source

Appliquons la formule de calcul de la puissance :

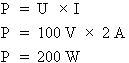
La puissance fournie par la source de tension est donc égale à 200 W.

Tout comme c'est le cas de la formule de la loi d'Ohm, on peut transformer la formule de la puissance pour isoler l'un ou l'autre des termes de l'équation :

• Si l'on divise par I les deux côtés de l'égalité, on obtient :

D'où : .

 

• Si l'on divise par U les deux côtés de l'égalité, on obtient :

D'où : .

Exemple qui montre comment utiliser cette dernière formule :

Problème: calculez la valeur du courant circulant dans une plinthe de chauffage électrique de 1 500 W, branchée à une source de 240 V.

• Identification des données

A la lecture du problème, on peut déterminer les valeurs connues et inconnues :

P  =  1 500 W, U = 240 V et I = ?

• Calcul de la valeur du courant

Pour calculer la valeur du courant circulant dans la plinthe, appliquons la formule suivante :

I  = P/U

I = 1 500 W/240 V, d'où I = 6,25 A.

Le courant circulant dans la plinthe a une intensité de 6,25 A.

La dissipation de puissance par une résistance se manifeste sous forme de chaleur. Ce phénomène est mis à profit dans plusieurs applications courantes (grille-pain, bouilloires, chauffage de la maison, etc.). La puissance dissipée par la résistance est fournie par la source.

Pour calculer la puissance dissipée par une résistance, il suffit de multiplier le courant traversant cette résistance par la tension à ses bornes.

Il est également possible de déterminer la puissance dissipée en utilisant la valeur de la résistance combinée à celle de la tension ou du courant. Il suffit alors de remplacer le courant ou la tension dans la formule de la puissance par son équivalence dans la loi d'Ohm.

• Remplacement du courant :

- Connaissant la loi d'Ohm :

.

- Connaissant la formule de la puissance :

.

- Si l'on remplace I dans la formule de la puissance par son équivalence dans la loi d'Ohm, on obtient :

• Remplacement de la tension :

- Connaissant la loi d'Ohm :

- On peut isoler la tension :

.

- Connaissant la formule de la puissance :

.

- Si l'on remplace U dans la formule de la puissance par son équivalence dans la loi d'Ohm, on obtient :

Exemples d'utilisation de ces formules :

Problème 1 : quelle sera la puissance dissipée par une résistance de 1 kΩ si elle est branchée à une source de 30 V ?

• Identification des données

Plaçons d'abord les données sous forme mathématique :

U = 30 V, R = 1 K ohms et P = ?

• Calcul de la valeur de la puissance dissipée par la résistance

Appliquons la formule de la puissance transformée précédemment :

P = U²/R.

P = (30 V) ²/1 K ohms d'où P = 0,9 W ou 900 mW.

La puissance dissipée par la résistance vaut donc 0,9 W ou 900 mW.

Problème 2 : quelle sera la puissance dissipée par une résistance de 100 Ω si elle est parcourue par un courant de 2,5 A ?

• Identification des données

La lecture du problème permet d'établir que :

I = 2,5 A, R = 100 ohms et P = ?

• Calcul de la valeur de la puissance dissipée par la résistance

Il ne reste qu'à appliquer la formule de la puissance transformée :

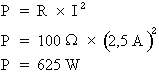
La puissance dissipée par la résistance s'élève à 625 W.