Exploitation de courbes d'évolution expérimentales

Le carbone 14 de l'atmosphère est assimilé par les végétaux au cours de la synthèse chlorophyllienne et par l'homme par le biais de l'alimentation et la respiration : la concentration en carbone 14 reste donc quasiment constante au cours de la vie de ces organismes.
A la mort de ces organismes, la quantité de carbone 14 n'est plus renouvelée et décroît par radioactivité.

1. Définir la demi-vie d'un noyau radioactif.
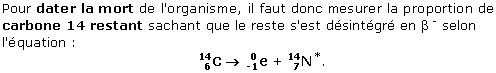
La demi-vie est le temps au bout duquel la moitié des noyaux radioactifs de l'échantillon de départ se sont désintégrés.

Comment la déterminer graphiquement sur une courbe du type N = f(t) exponentielle ?
Il faut se placer sur l'axe des ordonnées à N₀ / 2 (la moitié des noyaux se sont désintégrés) et projeter sur la courbe pour trouver l'abscisse temporelle correspondante : ce sera t_1/2 qu'il faudra convertir en seconde si ce n'est pas l'unité de l'échelle.

Quelle est la demi-vie du carbone 14 ?

Sur la courbe, à N₀ / 2, on note une abscisse t = t_1/2 ± 5 500 ans = 1,7.10¹¹ s.

 

 

3. Quel est le nombre de noyaux restants au bout de 11 140 années ?
D'après la courbe, il reste 250 noyaux au bout de 11 140 ans.

Quel est le rapport du nombre de noyaux restants par rapport au nombre de noyaux au départ ?
R = N / N₀ = 250 / 1000 = 1/4.

Combien de périodes radioactives se sont écoulées ?
11 140 / 5500 = 2,025 ± 2 périodes.

En vous basant sur l'exemple précédent, retrouver la relation littérale entre le nombre N de noyaux restants en fonction du nombre de noyaux de départ N₀ et du nombre k de périodes radioactives.
R = N / N₀ = 1/ 2 ², au bout de deux périodes, en généralisant on peut écrire qu'au bout de k périodes, il reste N noyaux radioactifs par rapport au nombre de noyaux N₀ de départ, tel que : N = N^₀ / (2^k).

4. Au bout de combien de périodes ne reste-t-il que 125 noyaux ?
Méthode 1 : Trouver le nombre d'années correspondantes : 16 710 ans et le nombre de périodes : 16 710 / 5 500 = 3,038 ± 3 périodes.

Méthode 2 : Utiliser la relation N = N₀ / (2^k) : N = 125 ; N₀ = 1 000 noyaux :
2^k = N₀ / N = 1 000 / 125 = 8 donc k = 3 périodes.

5. Dans un échantillon de statuette en bois, on détecte 1 atome de carbone 14 pour 16.10¹² atomes de carbone 12 alors qu'actuellement un échantillon de bois contient 1 atome de carbone 14 pour 10¹² atomes de carbone 12.
De combien d'années date la fabrication de la statuette (mort du bois utilisé pour la fabriquer) ?
Dans l'échantillon, il y a 1 atome de carbone 14 pour 16.10¹² atomes de carbone 12 alors qu'au départ les proportions devaient être les même qu'actuellement donc 1 atome de carbone 14 pour 10¹² atomes de carbone 12 ou 16 pour 16.10¹².
Donc la quantité de carbone 14 est passée de 16 à 1, ce qui représente 2⁴ donc 4 périodes radioactives, c'est-à-dire 4 x 5 500 ± 22 000 ans.

 

Attention : A en MBq = 10 ⁶ Bq et t en jours et non pas en secondes. 

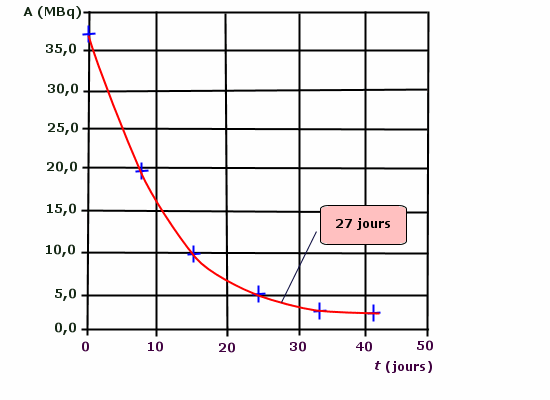
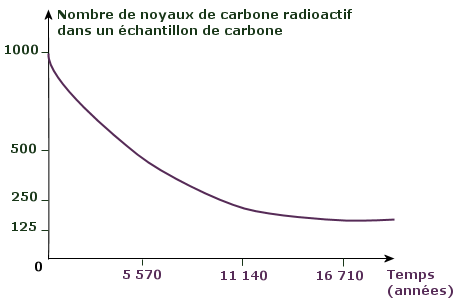
3. Sachant que la scintigraphie nécessite une solution d'iode 131 à 37 MBq, quelle est la masse d'iode 131 injectée ?
Si 1 g d'iode 131 possède une activité de 4,5.10⁹ MBq, alors la masse qui possède une activité de 37 MBq sera : m' = 1 x 37 / 4,5.10 ⁹ = 8,2.10^–9 g.

Que peut-on dire des quantités de nucléides radioactifs injectés aux patients ?
Les quantités injectées sont infimes pour ne pas irradier la matière.

4. Déterminer graphiquement la date t pour laquelle l'activité de départ sera divisée par 4.
A₀ = 37 MBq donc A₀ / 4 = 9,25 MBq, on trouve graphiquement t ± 17 jours = 1,47.10 ⁶ s.

5. Déterminer, grâce à la relation entre l'activité A mesurée et l'activité de départ A₀ (k étant le nombre de périodes écoulées) :
A = A₀ / (2^k), la date t pour laquelle l'activité de départ sera divisée par 4 et comparer ce résultat à celui de la question précédente.
A = A₀ / 4 = 9,25 MBq et A₀ = 37 MBq :
2 ^k = A₀ / A = 37 / 9,25 = 4 donc k = 2 périodes car 2^k = 4.
Le temps écoulé est de deux périodes : t = 2 x 8,1 = 16,2 jours.
Vu l'imprécision du graphique, la valeur de 17 jours estimée à la question précédente est du bon ordre de grandeur.

A la date t = 0, on dispose de N₀ noyaux de ¹³¹Po radioactif, à la date t il n'en reste que N non désintégrés :

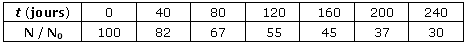
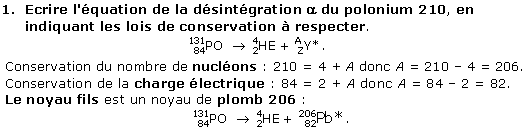
2. Tracer la courbe représentative de [- ln (N / N₀)] = f(t), les échelles sont :
1 cm pour 20 jours et 1 cm pour 0,1 en ordonnée.

 

 

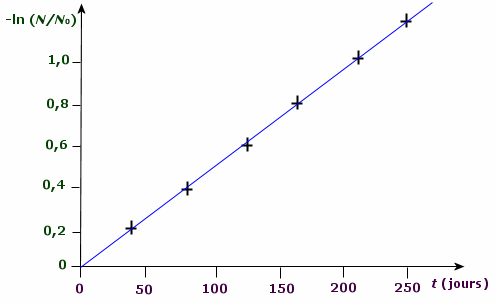
Quelle est le type de représentation graphique obtenue ?
La représentation graphique est celle d'une droite linéaire passant par l'origine.

Quelle est son équation en physique ?