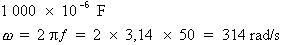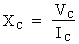Condensateur : introduction
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Le condensateur est un autre composant largement
utilisé dans les circuits électriques
et électroniques.
D'une façon similaire à la
bobine, le condensateur
placé dans un circuit à courant alternatif s'oppose,
par sa capacité, à la variation de tension
appliquée à ses bornes, en présentant une
réactance capacitive.
Cette
opposition provoque dans le condensateur un
déphasage qui se produit entre la
tension et le courant.
Illustration animée : Modèle de construction d'un condensateur.
Les matériaux couramment utilisés dans les condensateurs sont :
- le mica,
- le papier,
- la céramique,
- l'air.
Les condensateurs construits avec
ces matériaux sont dits non polarisés pour les
distinguer des condensateurs
électrolytiques.
Dans
les condensateurs électrolytiques, le matériau
diélectrique est une mince couche d'oxyde moléculaire.
Dans le but de conserver l'action électrolytique de
cette couche, la polarité des condensateurs est marquée
sur leurs bornes.
La capacité est la grandeur
caractéristique d'un condensateur. Elle correspond, en fait, au pouvoir qu'a ce
dernier d'emmagasiner de l'énergie. Ce pouvoir dépend
directement de la construction de chacun des
condensateurs.
Chaque
condensateur est caractérisé par sa capacité. Plus
sa capacité est grande, plus le condensateur peut
emmagasiner de l'énergie. La valeur de capacité d'un
condensateur est calculée à partir de sa
dimension physique et des matériaux utilisés
pour sa construction.
La formule suivante peut être
utilisée pour calculer la capacité d'un
condensateur :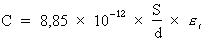 
Où : C : capacité en farads
(F)
S : surface des plaques en
mètres carrés (m2)
d : distance entre les deux
plaques en mètres (m)
er : constante
diélectrique correspondant au matériau séparant
les deux plaques
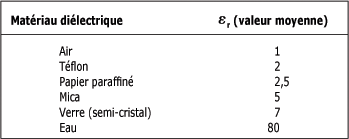
Les constantes diélectriques de quelques matériaux sont les suivantes :
La capacité d'un condensateur est symbolisée par C et son unité de mesure est le farad (F), donné en l'honneur du physicien anglais Michael Faraday. La représentation graphique d'un condensateur telle qu'elle apparaît dans les dessins de circuits électriques est :
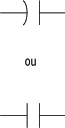
Dans le domaine du
commerce, deux notations sont utilisées par les
fabricants de condensateurs :
• µF (10-6 F);
• pF (10-12 F).
La capacité d'un condensateur peut être mesurée de façon précise par un capacimètre. Par ailleurs, l'état de fonctionnement d'un condensateur peut être vérifié à l'aide d'un ohmmètre.
Lorsqu'un ohmmètre est branché aux bornes d'un condensateur en bon état:
- la lecture de la résistance montre une valeur qui augmente graduellement pour s'arrêter à un niveau de l'ordre de méga-ohms.
Si un condensateur est défectueux à la suite d'un court-circuit entre les deux plaques ou d'une détérioration du matériau isolant qui sépare les plaques:
- la lecture de l'ohmmètre indiquera respectivement zéro ou une très faible valeur de résistance.
Lorsqu'un condensateur est placé dans un circuit à courant alternatif, il s'oppose à la variation de tension qui se trouve à ses bornes en présentant une réactance capacitive.
La valeur de la réactance capacitive d'un condensateur est déterminée par sa capacité et la fréquence de la tension appliquée à ses bornes.
La réactance capacitive,
symbolisée par XC, est exprimée
mathématiquement par la formule suivante :
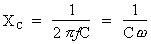. Où :
XC : réactance capacitive en ohms
Pi : la constante 3,14
f : fréquence du courant alternatif en hertz (Hz)
C : capacité du condensateur en farads (F): pulsation du courant alternatif en radians par seconde (rad/s)
Exemple de l'application
de cette formule :
Calculer la réactance capacitive, en ohms,
d'un condensateur dont la capacité est
de 1 000 µF lorsqu'une tension alternative d'une fréquence
de 50 Hz est appliquée à ses
bornes.
Formule pour
calculer la réactance capacitive : .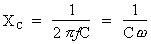
Où : Pi = 3,14, f = 50 Hz, C = 1 000 µF.
Ou :
Donc :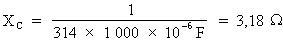 
La réactance capacitive du condensateur est égale à 3,18 Ohms.
Analyse des
résultats:
La valeur de la réactance capacitive
dépend:
- de la fréquence du courant alternatif;
- et de la capacité du condensateur.
Étant donné que la capacité d'un condensateur est une valeur fixe, la réactance capacitive ne peut varier qu'en fonction de la fréquence du courant alternatif.
Lorsqu'un condensateur est placé dans un circuit à courant alternatif, sa réactance capacitive dépend de la fréquence de la tension à ses bornes.
Par conséquent, on peut dire que si la fréquence varie, la réactance capacitive variera aussi mais d'une façon inversement proportionnelle:
- l'augmentation de la fréquence implique une diminution de la réactance capacitive,
- alors que la diminution de la fréquence implique une augmentation de la réactance capacitive.
Grâce à l'application de la loi d'Ohm, la relation entre le courant, la tension et la réactance capacitive peut être représentée par les formules suivantes :
ou
ou
Où : VC : tension alternative aux bornes du condensateur en volts (V)
IC : courant alternatif qui traverse le condensateur en ampères (A)
XC : réactance capacitive du condensateur en ohms
Exemple de l'application
de ces formules :
Lors de la mesure d'un circuit à courant
alternatif, on a obtenu une
lecture de tension de 220 volts aux bornes d'un
condensateur dont la capacité est
de 20 µF.
Calculez, en ampères (A), le courant du
condensateur pour chacune des fréquences
suivantes :
a) f = 50 Hz.
b) f = 120 Hz.
.
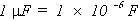Solution
•
Pour f = 50 Hz :
1e étape
Calcul de la
réactance capacitive : formule pour le calcul :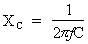 
.
Où : Pi = 3,14, f = 50 Hz, C = 20 µF.
Donc :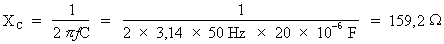 
.
2e étape
Calcul du
courant : formule pour le
calcul : .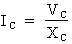
Où : VC = 220 volts et XC = 159,2 Ohms.
Donc :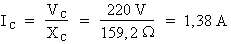 
.
Lorsque la fréquence du circuit est à 50 Hz, le courant du condensateur est égal à 1,38 A.
•
Pour f = 120 Hz :
1e
étape
Calcul de la
réactance capacitive : formule pour le calcul : .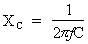
Où : Pi = 3,14, f = 120 Hz,
C = 20 µF.
Donc :
.
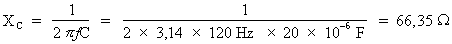Calcul du
courant : formule pour le
calcul : .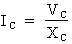
Où : VC = 220 volts et XC = 66,35 Ohms.
Donc :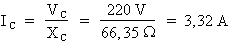 
.
Lorsque la fréquence est à 120 Hz, le courant du condensateur est égal à 3,32 A.
Vous pouvez constater que l'élévation de la fréquence a pour effet d'augmenter le passage du courant d'un condensateur:
Le courant d'un condensateur varie en proportion de la fréquence.
Cette raison explique pourquoi le condensateur est utilisé parfois dans les circuits électroniques pour éliminer des signaux (courants) de basse fréquence.
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fermer
Accédez gratuitement à
