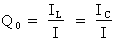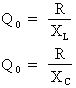Circuit RLC en parallèle (3)

Tout comme le circuit RLC en série, le circuit RLC en parallèle est aussi en résonance lorsque ses réactances s'annulent (X_L = X_C).

Toutefois, à cause de la configuration de ce circuit, la résonance d'un circuit RLC en parallèle ne produit pas les mêmes effets que celle d'un circuit RLC en série.

La résonance d'un circuit RLC en parallèle se produit lorsque les effets de chacune des réactances s'annulent (X_L = X_C).

L'impédance du circuit est alors purement résistive et est égale à la résistance. Z = R

Pour ce qui est des courants, lorsque X_L = X_C, le courant de la bobine doit, pour la même tension appliquée aux bornes de chacun des composants, être égal à celui du condensateur (I_L = I_C).

Par ailleurs, à cause du déphasage entre la tension et le courant dans chacun de ces composants, les courants I_L et I_C s'opposent et s'annulent. Ainsi le courant du circuit est égal au courant de la résistance et est en phase avec la tension appliquée. Ce courant peut être calculé grâce à l'une des formules suivantes : 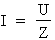 et

Où :

I : courant total du circuit en ampères (A)
U : tension appliquée au circuit en volts (V)
Z : impédance du circuit en ohms
R : résistance du circuit en ohms

La figuresuivante représente la relation de phase entre les courants et la tension d'un circuit RLC en parallèle lors de la résonance :

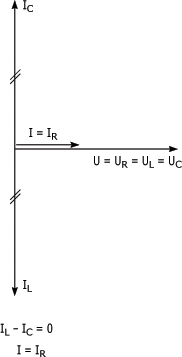
Problème : 

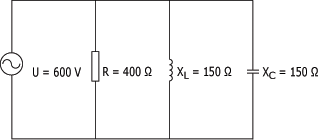
1. Pour le circuit en résonance ci-dessous, calculez :

a) Le courant de la bobine.
b) Le courant du condensateur.
c) Le courant de la résistance.
d) Le courant total.

2. Tracez le diagramme vectoriel de la tension et des courants de ce circuit.

1. Calculs des courants

a) Calcul du courant de la bobine :

Formule :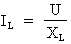

Où : U = 600 V ; X_L = 150 Ohms

Donc :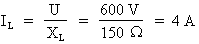

b) Calcul du courant du condensateur :

Formule :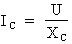

Où : U = 600 V ; X_C = 150 Ohms

Donc :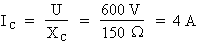

c) Calcul du courant de la résistance :

Formule :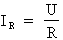

Où : U = 600 V ; R = 400 Ohms

Donc :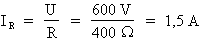

d) Calcul du courant total :

Formule :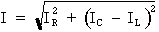

Où : I_R = 1,5 A ; I_C = 4 A ; I_L = 4 A

Donc :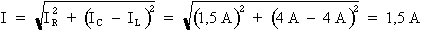

Le courant total du circuit est égal à 1,5 A, soit la même valeur que le courant de la résistance.

2. Diagramme de Fresnel

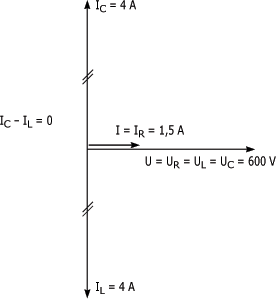
Cet exemple vous montre que lors de la résonance:

les courants dans les composants réactifs (I_L et I_C) peuvent être très élevés par rapport au courant total du circuit.

Ce phénomène est analogue à celui de la surtension lors de la résonance d'un circuit RLC en série.

Le cœfficient de surintensité d'un circuit RLC en parallèle, symbolisé par Q₀, se calcule par l'équation suivante :

Où :

I = I_R : courant du circuit à la résonance en ampères (A)
I_L : courant de la bobine en ampères (A)
I_C : courant du condensateur en ampères (A)
Q₀ : cœfficient de surintensité (sans unité)

Par ailleurs, ce cœfficient est le facteur de qualité du circuit, lequel peut être calculé par l'une des formules suivantes :

où

Q₀ : facteur de qualité (sans unité)
R : résistance du circuit en ohms
X_L : réactance inductive du circuit en ohms
X_C : réactance capacitive du circuit en ohms

Tout comme dans le cas de la résonance d'un circuit RLC en série, la fréquence de résonance dans un circuit RLC en parallèle, lorsque X_L = X_C, peut être déterminée.

Pour obtenir la formule de calcul de la fréquence de résonance, il est nécessaire de suivre le raisonnement suivant :

Si : X_L = X_C :

Alors : 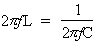 d'où :

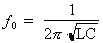
Où :

f₀ : fréquence de résonance en hertz (Hz)
L : inductance de la bobine en henrys (H)
C : capacité du condensateur en farads (F)

Jusqu'à maintenant, vous avez vu que la condition principale de la résonance ainsi que la fréquence de résonance d'un circuit RLC en parallèle sont identiques à celles d'un circuit RLC en série, c'est-à-dire que X_L = X_C et .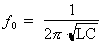

Attention, les effets qui se produisent lors de la résonance d'un circuit RLC en parallèle sont tout à fait contraires à ceux du circuit RLC en série.

Les courbes de résonance présentées ci-dessous vous montrent ces différences.

Courbes de résonance d'un circuit RLC en parallèle :

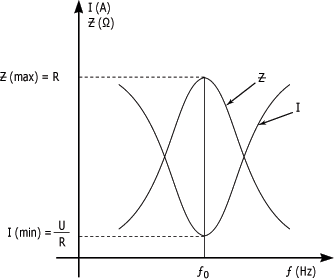
Sur la courbe du courant (I) de la figure, vous pouvez constater qu'à la fréquence de résonance f₀, le courant du circuit est à son minimum. Cependant, il augmente au fur et à mesure que la fréquence du circuit s'éloigne de sa valeur de résonance.

En effet, lorsque la fréquence est inférieure à sa valeur de résonance (f < f₀), le courant de la bobine est supérieur à celui du condensateur (car X_L < X_C).

Donc, le courant total du circuit augmente au-delà de sa valeur minimale pour satisfaire à la fois le courant de la résistance et la différence entre I_C et I_L (figure suivante). Ceci est également vrai lorsque la fréquence du circuit est supérieure à sa valeur de résonance (f > f₀).

Sur les courbes de résonance, vous retrouvez également la courbe Z qui représente la variation de l'impédance du circuit en fonction de la fréquence.

Cette courbe montre que l'impédance du circuit est à son maximum à la fréquence de résonance (car I est à son minimum) et qu'elle diminue graduellement lorsque la fréquence du circuit s'éloigne de sa valeur de résonance.

Courants du circuit RLC en parallèle en dehors de la fréquence de résonance :

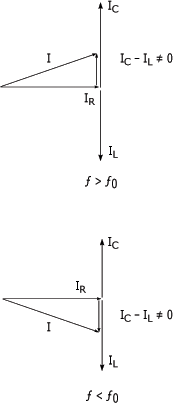
Tout comme dans le cas des circuits RLC en série:

les puissances réactives Q_L et Q_C d'un circuit RLC en parallèle s'annulent mutuellement lors de la résonance.

De plus, la puissance apparente est égale à la puissance active, laquelle est consommée par la résistance du circuit :

Si : QL = QC = 0

Alors :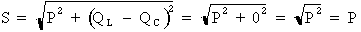

Par conséquent, le facteur de puissance du circuit est égal à l'unité :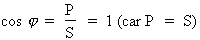

A la résonance, l'ensemble R, L et C constitue un circuit bouchon dont l'impédance atteint une grande valeur.

Une des applications du circuit résonant en parallèle est le filtre éliminateur de bande montré à la partie a de la figure suivante :

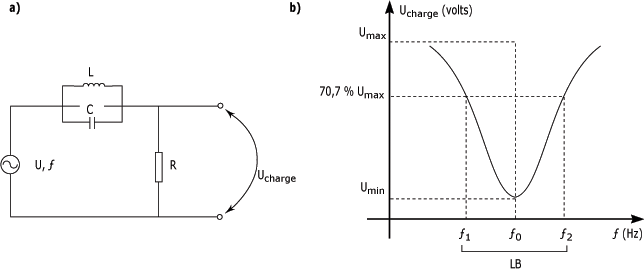
La fonction de ce type de filtre est d'éliminer les signaux de fréquence de résonance. En effet, à la fréquence de résonance, l'impédance équivalente du circuit composé de L et C est à son maximum, de telle sorte qu'une chute de tension maximale se retrouve aux bornes de L et C.

Par conséquent, seule une tension minimale de sortie se retrouve aux bornes de la résistance R. Cependant, lorsque la fréquence du circuit s'éloigne de sa valeur de résonance, l'impédance équivalente du circuit composé de L et C est diminuée et permet une chute de tension plus grande aux bornes de la résistance.

Ce type de filtre peut être éventuellement considéré comme le complément du filtre passe-bande. Sa largeur de bande éliminatrice, (LB) est limitée par les fréquences où la tension tombe à 70,7 % de sa valeur maximale (partie b de la figure 5.56).

En résumé sur le circuit RLC en parallèle :

Après avoir étudié le contenu de cette étude, vous devriez retenir plus particulièrement les points suivants :

• Dans un circuit RLC en parallèle, la tension aux bornes de chacun des composants est la même que la tension appliquée au circuit, c'est-à-dire que : U = U_R = U_L = U_C

• La relation entre les courants dans un circuit RLC en parallèle peut être exprimée par l'équation :

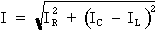
• Lorsque la réactance inductive est plus grande que la réactance capacitive (X_L > X_C), on observe les faits suivants :

- le courant de la bobine est inférieur à celui du condensateur (I_L < I_C) ;

- le courant total du circuit est en avance de phase par rapport à la tension appliquée ;

- le circuit réagit comme un circuit partiellement capacitif ;

- le facteur de puissance est un facteur capacitif.

• Lorsque la réactance inductive est plus petite que la réactance capacitive (X_L < X_C), on note les faits suivants :

- le courant de la bobine est supérieur à celui du condensateur (I_L > I_C) ;

- le courant total du circuit est en retard de phase par rapport à la tension appliquée ;

- le circuit réagit comme un circuit partiellement inductif ;

- le facteur de puissance est un facteur inductif.

• Lorsque la réactance inductive est égale à la réactance capacitive (X_L = X_C), on constate les faits suivants :

- les courants dans les composants réactifs s'annulent (I_C - I_L = 0) ;

- le courant du circuit est à son minimum et est en phase avec la tension appliquée ;

- l'impédance du circuit est à son maximum ;

- le facteur de puissance est égal à l'unité.

• La correction du facteur de puissance par l'ajout d'un condensateur raccordé en parallèle dans le circuit est plus avantageuse que la correction par l'ajout d'un condensateur raccordé en série. En effet, elle permet de réduire le courant total du circuit tout en rapprochant le facteur de puissance de l'unité.

Pour compléter ce résumé, voici un tableau récapitulatif des notions étudiées dans l'étude sur le circuit RLC en parallèle. Il vous présente les principales caractéristiques d'un circuit RLC en parallèle.

Tableau récapitulatif des caractéristiques du circuit RLC en parallèle :

Ce résumé termine cette étude portant sur les circuits RLC en parallèle.