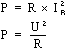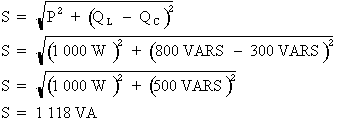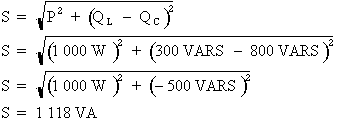Circuit RLC en parallèle (2)

Il a déjà été mentionné que les puissances dans un circuit à courant alternatif sont indépendantes du genre de raccordement.

Que les composants du circuit soient raccordés en série ou en parallèle:

• la puissance active est toujours engendrée par la résistance,
• la puissance réactive est associée à la bobine et au condensateur,
• et la puissance apparente représente la totalité des puissances du circuit.

La puissance active d'un circuit RLC peut être calculée à l'aide de l'une des formules suivantes :

Où :

P : puissance active du circuit en watts (W)
R : résistance du circuit en ohms
I_R : courant de la résistance en ampères (A)
U : tension appliquée au circuit en volts (V)

La puissance réactive associée au condensateur et celle associée à la bobine sont respectivement calculées par les formules qui suivent :

 Ou :   ou ou  ou

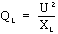
Q_C : puissance réactive du condensateur en VARS
Q_L : puissance réactive de la bobine en VARS
X_C : réactance capacitive du condensateur en ohms
X_L : réactance inductive de la bobine en ohms
I_C : courant du condensateur en ampères (A)
I_L : courant de la bobine en ampères (A)
U : tension appliquée au circuit en volts (V)

Puisque la tension est la même aux bornes du condensateur et de la bobine, et compte tenu du déphasage du courant par rapport à la tension dans chacun des composants, la relation de phase entre la puissance réactive du condensateur et celle de la bobine par rapport à la tension peut être représentée par les vecteurs montrés à la figure suivante.

Puissances réactives dans un circuit RLC en parallèle :

Tout comme celle d'un circuit RLC en série, la puissance réactive totale d'un circuit RLC en parallèle est obtenue par la différence entre la puissance réactive du condensateur et la puissance réactive de la bobine : Q_T = Q_L - Q_C

Où :

Q_T : puissance réactive totale du circuit en VARS
Q_C : puissance réactive du condensateur en VARS
Q_L : puissance réactive de la bobine en VARS

Par définition, la puissance apparente est la puissance totale du circuit, puisqu'elle correspond à la puissance fournie par la source :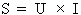

Où :

S: puissance apparente du circuit en VA
U : tension appliquée au circuit en volts (V)
I : courant total du circuit en ampères (A)

Dans un circuit RLC en parallèle, la puissance apparente peut être calculée par :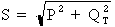

D'où : 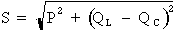(car : Q_T = Q_L - Q_C)

Où :

S : puissance apparente du circuit en VA
P : puissance active du circuit en watts (W)
Q_C : puissance réactive du condensateur en VARS
Q_L :puissance réactive de la bobine en VARS
Q_T : puissance réactive totale du circuit en VARS

Dans un circuit RLC en parallèle, on sait que Q_L peut être soit plus grand, soit plus petit que Q_C. Peu importe le rapport de grandeur entre Q_L et Q_C, cette formule est toujours valable, puisque la différence entre ces deux valeurs élevées au carré est toujours positive.

Selon que Q_L > Q_C ou Q_L < Q_C, le triangle des puissances d'un circuit RLC en parallèle diffère. La figure suivante présente le triangle des puissances de chacune de ces possibilités.

Triangles des puissances d'un circuit RLC en parallèle :

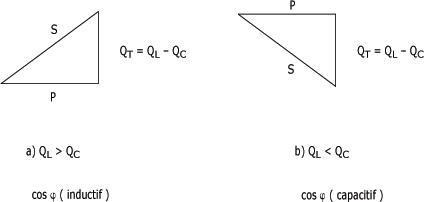
Le facteur de puissance est calculé grâce à la formule : .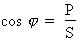
Tout comme le circuit RLC en série, lorsque Q_L > Q_C, le circuit RLC en parallèle se comporte comme un circuit surtout inductif et son facteur de puissance est lui aussi inductif.

Par contre, dans le cas où Q_L < Q_C, le facteur de puissance du circuit ainsi que son comportement sont capacitifs.

Voici un exemple du calcul des puissances d'un circuit RLC en parallèle.

Problème :

Pour le circuit suivant :

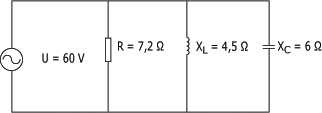
1. Calculez la puissance apparente du circuit.
2. Calculez le facteur de puissance du circuit et précisez s'il est inductif ou capacitif.
3. Dessinez le triangle des puissances du circuit.

Solutions :

1. Calcul de la puissance apparente

1^e étape. Calcul de la puissance active :

Formule :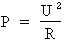

Où : U = 60 V ; R = 7,2 Ohms

Donc :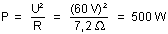

2^e étape. Calcul de la puissance réactive de la bobine :

Formule :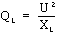

Où : U = 60 V ; X_L = 4,5 Ohms

Donc :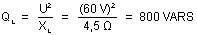

3^e étape. Calcul de la puissance réactive du condensateur :

Formule :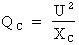

Où : U = 60 V ; X_C = 6 Ohms

Donc :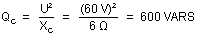

4^e étape. Calcul de la puissance apparente :

Formule :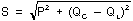

Où : P = 500 W ; Q_C = 600 VARS ; Q_L = 800 VARS

Donc :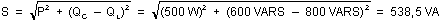

La puissance apparente du circuit est égale à 538,5 VA.

2. Calcul du facteur de puissance :

Formule :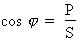

Où : P = 500 W ; S = 538,5 VA

Donc :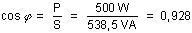

Le facteur de puissance du circuit est égal à 0,928 et est inductif, car Q_L > Q_C.

3. Triangle des puissances

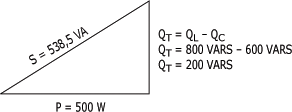
Problème :
Calculez le facteur de puissance pour chacun des circuits présentant les données suivantes et préciser s'il s'agit d'un facteur inductif ou capacitif.

1. P = 1 000 W, Q_L = 800 VARS et Q_C = 300 VARS
2. P = 1 000 W, Q_L = 300 VARS et Q_C = 800 VARS

Solutions :

1.

1^e étape. Calcul de la puissance apparente :

Formule :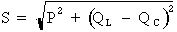

Où : P = 1 000 W, Q_L = 800 VARS et Q_C = 300 VARS

Donc :

2^e étape. Calcul du facteur de puissance :

Formule :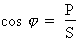

Où : P = 1 000 W et S = 1 118 VA

Donc :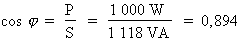

Le facteur de puissance pour ce circuit est égal à 0,894 et est inductif, car Q_L > Q_C.

2.

1^e étape

Calcul de la puissance apparente :

Formule :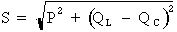

Où : P = 1 000 W, Q_L = 300 VARS et Q_C = 800 VARS

Donc :

2^e étape. Calcul du facteur de puissance :

Formule :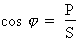

Où : P = 1 000 W et S = 1 118 VA

Donc :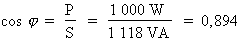

Le facteur de puissance pour ce circuit est égal à 0,894 et il est capacitif, car Q_L < Q_C.

Dans cet exemple, vous pouvez remarquer que la valeur du facteur de puissance est la même pour les deux circuits.

Pourtant, ces facteurs de puissance ne sont pas de même nature, puisque selon la relation de grandeur entre Q_L et Q_C, le facteur est soit inductif, soit capacitif.

Problème :
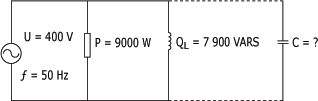
Le circuit de la figure suivante représente un circuit inductif en parallèle dont la correction du facteur de puissance se fera par l'ajout d'un condensateur raccordé en parallèle.

1. Calculez le facteur de puissance du circuit avant l'ajout du condensateur.
2. Calculez le courant du circuit avant l'ajout du condensateur.
3. Calculez la capacité du condensateur à raccorder dans le circuit pour obtenir un facteur de puissance proche (plus grand ou égal) de 0,9.
4. Calculez le courant du circuit après la correction du facteur de puissance.

Solutions :

1. Calcul du facteur de puissance

1^e étape. Calcul de la puissance apparente :

Formule :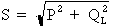

Où : P = 9 000 W ; Q_L = 7 900 VARS

Donc :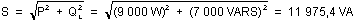

2^e étape. Calcul du facteur de puissance :

Formule :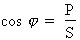

Où : P = 9 000 W ; S = 11 975,4 VA

Donc :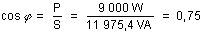

Le facteur de puissance du circuit avant l'ajout du condensateur est égal à 0,75.

2. Calcul du courant du circuit avant l'ajout du condensateur :

Si :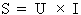

Alors :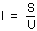

Formule :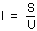

Où : S = 11 975,4 VA ; U = 400 V

Donc :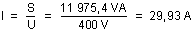

Le courant du circuit avant l'ajout du condensateur est égal à 29,93 A.

3. Calcul de la capacité du condensateur à raccorder

1^e étape. Calcul de la puissance apparente :

Le but de la correction du facteur de puissance est de réduire la puissance apparente tout en satisfaisant la demande de consommation du circuit. Ainsi, on peut supposer que la puissance active du circuit est toujours la même et par conséquent établir la relation suivante :

Si : 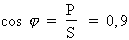 alors :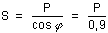

Formule :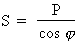

Où :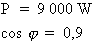

Donc :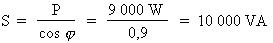

2^e étape. Calcul de la puissance réactive totale du circuit :

Si : S² = P² + Q_T²

Alors : Q_T² = S² - P²

Donc :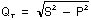

Formule :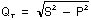

Où : S = 10 000 VA ; P = 9 000 W

Donc :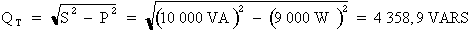

3^e étape. Calcul de la puissance réactive du condensateur :

Étant donné que la puissance réactive existante du circuit est inductive et égale à 7 900 VARS, pour ramener la puissance réactive du circuit à 4 358,9 VARS, le condensateur à raccorder doit contribuer une puissance réactive calculée comme suit :

Si Q_T = Q_L - Q_{C a}lors : Q_C = Q_L - Q_T

Où : Q_L= 7 900 VARS ; Q_T = 4 358,9 VARS

Donc : Q_C = Q_L - Q_T = 7 900 VARS - 4 358,9 VARS = 3 541,1 VARS

4^e étape. Calcul de la réactance capacitive du condensateur :

Si : 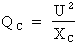 alors :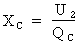

Où : U = 400 V ; Q_C = 3 541,1 VARS

Donc :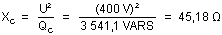

5^e étape. Calcul de la capacité du condensateur :

Si : 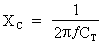 alors :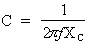

Où : Pi = 3,14 ; f = 50 Hz ; X_C = 45,18 Ohms

Donc : 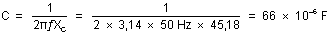 = 66 µF

Le condensateur à ajouter dans le circuit pour corriger le facteur de puissance à 0,9 doit avoir une capacité de 66 µF.

4. Calcul du courant du circuit après la correction du facteur de puissance :

Si :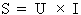

Alors :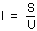

Où : S = 10 000 VA ; U = 400 V

Donc :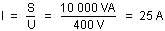

Le courant du circuit après la correction du facteur de puissance est égal à 25 A.

Vous avez vu à l'étude sur le circuit RLC en série que la correction du facteur de puissance pour un circuit partiellement inductif peut être réalisée par l'ajout d'un condensateur raccordé en série.

Cet ajout améliore effectivement le facteur de puissance du circuit, mais a l'inconvénient de provoquer l'augmentation du courant du circuit.

L'exemple qui suit montre une autre façon de corriger le facteur de puissance d'un circuit inductif par l'ajout d'un condensateur raccordé en parallèle.

Cet exemple démontre bien que l'ajout d'un condensateur raccordé en parallèle permet non seulement la correction du facteur de puissance mais également la diminution du courant.

En effet, pour une même puissance consommée par le circuit, soit 9 000 W, la source doit fournir avant l'ajout du condensateur une tension de 400 V et un courant de 29,93 A, alors qu'après l'ajout, elle fournit toujours une tension de 400 V mais seulement un courant de 25 A.

C'est pourquoi cette méthode de correction du facteur de puissance est utilisée fréquemment pour les installations représentant de nombreuses charges inductives (moteurs, fours à induction, ballast d'éclairage…) afin de pouvoir réduire l'intensité du courant à transporter.