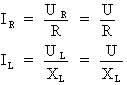Circuit RL en parallèle (1)

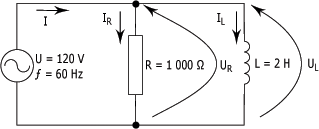
Un circuit RL en parallèle est un circuit composé d'une résistance raccordée en parallèle à une bobine, comme le montre la figure suivante :

Dans cette étude, vous approfondirez vos connaissances des circuits inductifs en étudiant les notions relatives aux circuits RL en parallèle.

Vous apprendrez ce que représentent, dans ce type de circuit :

• l'impédance,
• la relation de phase entre la tension et le courant,
• les puissances,
• le facteur de puissance.

Enfin, vous verrez les différentes formules nécessaires pour leur calcul.

L'impédance d'un circuit RL en parallèle, tout comme celle de tout autre circuit à courant alternatif, est toujours définie par le rapport entre la tension totale et le courant total du circuit. Cet énoncé peut être exprimé par la formule suivante : .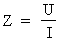

En fait, l'impédance de ce type de circuit correspond à l'opposition combinée de la résistance et de la réactance inductive du circuit lors du passage d'un courant alternatif. La formule suivante permet de déterminer l'impédance d'un circuit RL en parallèle : .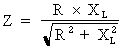
Où :

Z : impédance totale en ohms
R : résistance en ohms
X_L : réactance inductive en ohms

Application de cette formule :
Pour le circuit de la figure ci-dessous, calculez :

a) l'impédance totale du circuit ;
b) le courant total du circuit.

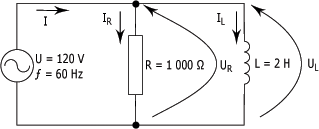
Solution :

a) Calcul de l'impédance totale

1^e étape

Calcul de la réactance inductive : formule pour le calcul : X_L = 2xPixfxL.

Où : Pi = 3,14, f = 60 Hz, L = 2 H

Donc :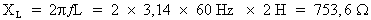

2^e étape

Calcul de l'impédance totale du circuit :

Formule pour le calcul :

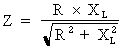
Où : R = 1 000 Ohms et X_L = 753,6 Ohms

Donc :

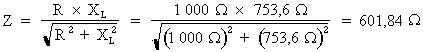
L'impédance totale du circuit est égale à 601,84 Ohms.

b) Calcul du courant total : formule pour le calcul : si : .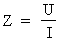
Alors :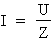

Où : U = 120 V et Z = 601,84 Ohms.
Donc :

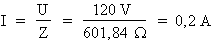
Le courant total du circuit est égal à 0,2 A.

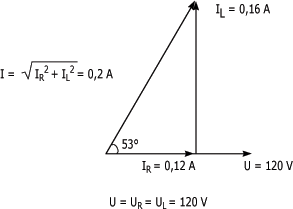
Une des principales caractéristiques d'un circuit en parallèle est la parité des tension. En effet, dans un circuit RL en parallèle, la valeur de la tension aux bornes de la résistance (U_R) est toujours égale à la valeur de la tension aux bornes de la bobine (U_L).

Cette valeur équivaut également à la valeur de la tension d'alimentation (U). Ainsi, on peut dire que U_R = U_L = U.

Cependant, la valeur du courant qui circule dans chacun des composants R et L dépend de l'opposition présentée par chacun d'eux. Il y a donc respectivement le courant de la résistance (I_R) et celui de la bobine (I_L).

Étant donné que la valeur de la tension est la même pour les deux composants, en l'occurrence R et L, il est permis de dire, si l'on prend la tension comme référence, que le courant de la bobine (I_L) est en retard de 90° par rapport à celui de la résistance (I_R). Le diagramme de Fresnel de la figure suivante représente ces relations.

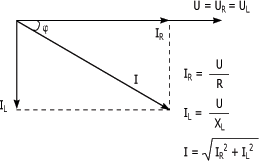
Le courant total du circuit peut donc être obtenu par la somme vectorielle des courants I_R et I_L, exprimée mathématiquement par l'équation suivante : .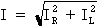

Où :

I : courant total du circuit en ampères (A)
I_R : courant de la résistance en ampères (A)
I_L : courant de la bobine en ampères (A)

Sachant que la loi d'Ohm peut être appliquée aux circuits à courant alternatif, il est possible de calculer le courant qui circule dans chacun des composants R et L en utilisant respectivement les formules suivantes :

Où : U = U_R = U_L

U_R : tension aux bornes de la résistance en volts (V)
U_L : tension aux bornes de la bobine en volts (V)
U : tension d'alimentation en volts (V)

Calcul de courant d'un circuit RL en parallèle :
Pour le circuit de la figure ci-dessous, calculez :

a) le courant qui circule dans chacun des composants R et L ;
b) le courant total.

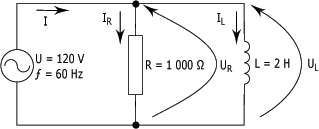
Solution :

a) Calcul du courant dans chacun des composants

- Courant de la résistance : formule pour le calcul :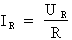

Où : U_R = 120 V puisque U = 120 V et R = 1 000 Ohms

Donc :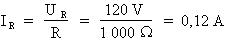

Le courant de la résistance est égal à 0,12 A.

- Courant de la bobine : formule pour le calcul :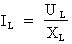

Où : U_L = 120 V puisque U = 120 V et X_L = 753,6 Ohms (calculée précédemment)

Donc :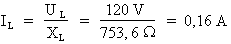

Le courant de la bobine est égal à 0,16 A.

b) Calcul du courant total : formule pour le calcul :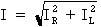

Où : I_R = 0,12 A et I_L = 0,16 A

Donc :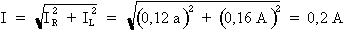

Le courant total du circuit est égal à 0,2 A.

Une approche pratique au problème de calcul de l'impédance des circuits RL en parallèle consiste à calculer d'abord le courant total du circuit, puis appliquer simplement la loi d'Ohm par l'utilisation de l'équation: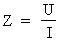

Cette façon de faire évite l'emploi de la formule complexe de l'impédance.

En vous reportant à la figure 3.15, vous pouvez constater que le courant total du circuit n'est pas en phase avec la tension d'alimentation.

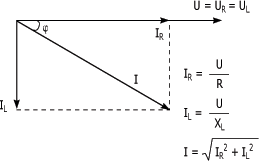
Effectivement, il est déphasé d'un angle 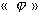 par rapport à la tension d'alimentation. Cet angle peut être calculé par la formule suivante : .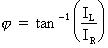
Où :

 : angle de déphasage en degrés (°)
tan^-1 : fonction trigonométrique de l'arc de la tangente
I_L : courant de la bobine en ampères (A)
I_R : courant de la résistance en ampères (A)

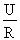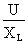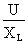Comme les courants I_R et I_L sont déterminés respectivement par les rapports  et , l'angle de déphasage peut alors être déterminé à partir de la résistance et de la réactance inductive. En effet, en remplaçant respectivement dans la formule précédente I_L et I_R par les rapports  et 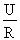, on obtient :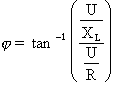

Or, on peut dire que :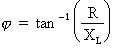  

Comme dans le circuit RL en série, le courant total d'un circuit RL en parallèle est toujours en retard de phase par rapport à la tension appliquée au circuit. Ce déphasage est représenté par un angle compris entre 0 et 90°. Cependant, contrairement au circuit RL en série, l'angle de déphasage d'un circuit RL en parallèle n'est pas caractérisé par le rapport 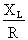, mais plutôt par celui de .

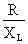Application des notions relatives à l'angle de déphasage d'un circuit RL en parallèle :

1. Pour le circuit ci-dessous, calculez, en degrés (°), l'angle de déphasage à partir :

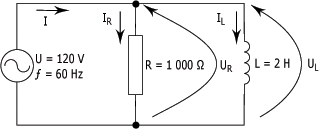
a) de la résistance et de la réactance inductive ;

b) des valeurs de courant calculées à l'exemple précédent.

2. Tracez le diagramme de Fresnel des courants et de la tension du circuit de la figure.

Solution :

1. Calcul de l'angle de déphasage

a) A partir de la résistance et de la réactance inductive : formule pour le calcul :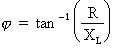
Où : R = 1 000 Ω et X_L = 753,6 Ω (calculée précédemment)

Donc :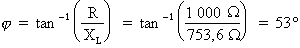

b) A partir des valeurs de courant : formule pour le calcul :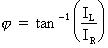
Où : I_L = 0,16 A (calculé précédemment) et I_R = 0,12 A (calculé précédemment)
Donc :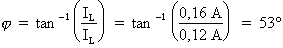

Que l'une ou l'autre de ces formules soit appliquée, le calcul de l'angle de déphasage donne 53°.

2. Diagramme de Fresnel