Autres exemples de croissance
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Soit la suite u définie par un = n² + n + 1.
u0 = 0 + 0 + 1 = 1 ;
u1 = 1² + 1 + 1 = 3 ;
u2 = 2² + 2 + 1 = 4 + 2 + 1 = 7 ;
u3 = 3² + 3 + 1 = 9 + 3 + 1 = 13.
A l'aide d'un tableur, on calcule facilement autant de termes que l'on veut :
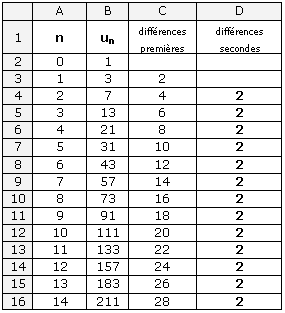
On peut faire l'expérience suivante :
o calcul des « différences
premières » :
En cellule C3, on calcule u1 -
u0 (= B3 - B2), on recopie la formule vers le
bas et on obtient donc en colonne C, les nombres
u1 - u0,
u2 - u1,
u3 - u2, etc ;
o calcul des « différences
secondes » :
Dans la colonne D, on calcule les différences entre 2
termes consécutifs de la colonne C. La formule
placée dans la cellule D4 est égale
à C4 - C3.
Les différences secondes jusqu'au rang 14 sont toutes
égales à 2.
Ce résultat est vrai pour toutes les valeurs de
n. En effet :
Pour tout n, un+1 -
un = [(n + 1)² + (n +
1) + 1] - [n² + n + 1] = 2n +
2.
Les différences premières sont donc, pour tout
n, de la forme 2n + 2 ; ce sont donc les termes
d'une suite arithmétique de raison 2 et donc la
différence entre deux termes consécutifs est
toujours 2.
La suite étudiée est dite une suite à différences secondes constantes.
On peut faire la même expérience et le même raisonnement avec toute suite du type un = an² + bn + c où a, b et c sont des nombres quelconques.
o les deux premiers termes sont égaux à 1 ;
o chaque terme de la suite est égal à la somme des deux termes qui le précèdent.
Les premiers termes de la suite sont : 1, 1, 2, 3, 5, 8, 13, 21, 34, etc.
Un tableur permet de calculer rapidement autant de termes de la suite que l'on veut :

Si l'on calcule pour chaque valeur de n le rapport un+1 / un, on obtient :
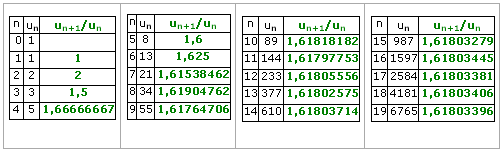
On observe que ces rapports ne sont pas égaux, mais qu'ils sont de plus en plus proches les uns des autres. A partir du rang 9, leurs arrondis au millième sont égaux à 1,618.
Il est intéressant d'observer la suite obtenue en changeant les deux premiers termes de la suite de Fibonacci. Si les premiers termes sont 1 et 3, on obtient :
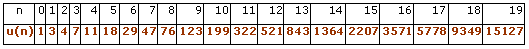
Voici le tableau donnant le rapport entre deux termes consécutifs :
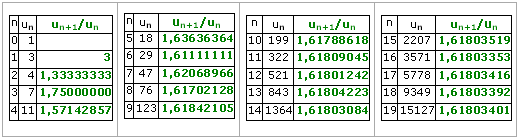
A partir du rang 9, leurs arrondis au millième sont, eux aussi, égaux à 1,618.
On démontre que lorsque n augmente, ce rapport est de plus en plus proche du nombre d'or.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !







