Matrices et opérations
- Fiche de cours
- Quiz
- Profs en ligne
- Videos
- Application mobile
Objectif(s)
Donner les définitions définitives concernant
les matrices.
Définir les opérations sur les matrices.
Définir les opérations sur les matrices.
1. Définitions, vocabulaires et notations
a. Définition 1 : matrice
Soit (m, n) un couple d’entiers
naturels non nuls.
On appelle matrice de dimension m × n (on ne calcule pas la valeur de ce produit ) ou de format (m ; n), tout tableau rectangulaire de m × n nombres, appelés coefficients de la matrice.
Ces coefficients sont disposés sur m lignes et n colonnes.
On appelle matrice de dimension m × n (on ne calcule pas la valeur de ce produit ) ou de format (m ; n), tout tableau rectangulaire de m × n nombres, appelés coefficients de la matrice.
Ces coefficients sont disposés sur m lignes et n colonnes.
On note une matrice par une lettre majuscule et ses coefficients par la même lettre minuscule à laquelle on affecte deux indices, le premier représentant le numéro de la ligne et le second représentant le numéro de la colonne.
Par exemple, on écrit :
On peut aussi écrire : A = (ai,j) avec (i,j) couple d’entiers vérifiant 1 ≤ i ≤ m et 1 ≤ j ≤ n.
Le coefficient général ai,j est le nombre situé à l’intersection de la i-ième ligne et la j-ième colonne.
b. Définition 2 : matrices
particulières
• La matrice
nulle est la matrice dont tous les
coefficients sont nuls. On la note 0.
• La matrice (ai,1, ai,2, …, ai,n) est la matrice ligne de rang i de la matrice A ; on l’appelle encore vecteur ligne de rang i.
• La matrice colonne de rang j de la matrice A est aussi appelée vecteur colonne de rang j.
On la note :
.
• La matrice (ai,1, ai,2, …, ai,n) est la matrice ligne de rang i de la matrice A ; on l’appelle encore vecteur ligne de rang i.
• La matrice colonne de rang j de la matrice A est aussi appelée vecteur colonne de rang j.
On la note :
.
c. Définition 3 : égalité de
deux matrices
On dit que deux matrices A et B
sont égales lorsqu’elles ont la
même dimension et pour tout couple (i,
j), on dispose de l’égalité
ai,j
= bi,j. Ainsi, on note
A = B.
Remarque
Si A et B ne sont pas égales alors soit elles n’ont pas la même dimension soit il existe un couple (i,j) pour lequel ai,j ≠ bi,j. On note A ≠ B.
2. Addiction matricielle : multiplication d'une matrice
par un nombre
a. Addition de deux matrices
Pour tout couple (A, B) de matrices de
même dimension m × n, on
appelle addition ou somme
de A et de B, et l’on note
A + B, la matrice S de
dimension m × n
vérifiant
si,j =
ai,j +
bi,j,
pour tout couple (i ; j) tels que
1 ≤ i ≤ m et
1 ≤ j ≤ n.
Remarque
A + B = B + A.
b. Multiplication d'une matrice par un nombre
Soit A une matrice de dimension m ×
n.
Pour tout réel k, la matrice de coefficient général k × ai,j est la matrice dont tous les coefficients de la matrice A ont été multipliés par le nombre k.
Cette nouvelle matrice est de dimension m × n et on la note kA.
Exemple :Pour tout réel k, la matrice de coefficient général k × ai,j est la matrice dont tous les coefficients de la matrice A ont été multipliés par le nombre k.
Cette nouvelle matrice est de dimension m × n et on la note kA.
Soient
.Calculer C = A + 2B.
Remarque
A + (–1)B se note A – B et B + (–B) = 0.
3. Multiplication de deux matrices
Cette opération est un peu plus compliquée
à définir.
On va donc commencer par deux exemples formateurs.
• Exemple 1 :
Soient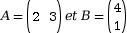
. A est de dimension 1
× 2 et B, de dimension 2 × 1.
On peut multiplier A par B.
A a autant de colonnes que B a de lignes. On obtient donc une matrice de dimension 1 × 1 que l'on note A × B ou AB.
On procède ainsi :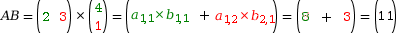
.
• Exemple 2 :
Soient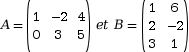
. A est de dimension 2
× 3 et B, 3 × 2.
On peut multiplier A par B.
A a autant de colonnes que B a de lignes. On obtient donc une matrice de dimension 2 × 2.
Posons P la matrice produit AB et détaillons le calcul de chacun de ses coefficients.
pi,j se calcule à l’aide du vecteur ligne de rang i de A et le vecteur colonne de rang j de B.
On procède alors comme dans l’exemple 1 :
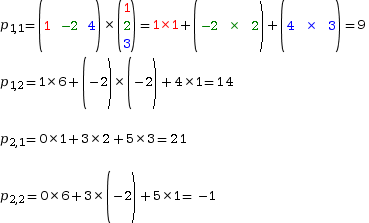
Donc : P = AB =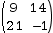
.
Pour calculer AB, on aurait pu placer les matrices comme ci-dessous :
.
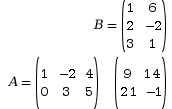
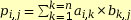Remarques
La calculatrice et des logiciels spécifiques pourront vous aider à calculer ces produits, surtout quand les dimensions sont « grandes ».
Il faut faire très attention aux dimensions.
On va donc commencer par deux exemples formateurs.
• Exemple 1 :
Soient
. A est de dimension 1
× 2 et B, de dimension 2 × 1.On peut multiplier A par B.
A a autant de colonnes que B a de lignes. On obtient donc une matrice de dimension 1 × 1 que l'on note A × B ou AB.
On procède ainsi :
.• Exemple 2 :
Soient
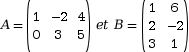. A est de dimension 2
× 3 et B, 3 × 2.On peut multiplier A par B.
A a autant de colonnes que B a de lignes. On obtient donc une matrice de dimension 2 × 2.
Posons P la matrice produit AB et détaillons le calcul de chacun de ses coefficients.
pi,j se calcule à l’aide du vecteur ligne de rang i de A et le vecteur colonne de rang j de B.
On procède alors comme dans l’exemple 1 :
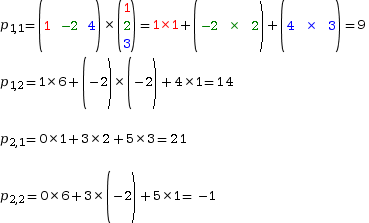
Donc : P = AB =
.Pour calculer AB, on aurait pu placer les matrices comme ci-dessous :
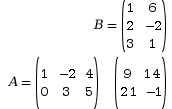
Soit A une matrice de dimension m ×
n.
Soit B une matrice de dimension n × p.
Soit B une matrice de dimension n × p.
La multiplication de la matrice A à
n colonnes, par la matrice B à
n lignes, est la matrice produit
P, notée A
× B ou plus simplement
AB.
C’est une matrice de dimension m × p et de coefficient général, défini à l’aide du vecteur ligne de rang i de A et du vecteur colonne de rang j de B, est égal à :
C’est une matrice de dimension m × p et de coefficient général, défini à l’aide du vecteur ligne de rang i de A et du vecteur colonne de rang j de B, est égal à :
.
Remarques
La calculatrice et des logiciels spécifiques pourront vous aider à calculer ces produits, surtout quand les dimensions sont « grandes ».
Il faut faire très attention aux dimensions.
Comment as-tu trouvé ce cours ?
Évalue ce cours !
Vous avez obtenu75%de bonnes réponses !
Recevez l'intégralité des bonnes réponses ainsi que les rappels de cours associés :
Fiches de cours les plus recherchées
Mathématiques
Matrices carrées
Mathématiques
Matrices inverses
Mathématiques
Dérivées des fonctions sinus et cosinus
Mathématiques
Suites géométriques et arithmético-géométriques
Mathématiques
Loi normale centrée réduite N(0,1)
Mathématiques
Fonction convexe et fonction concave sur un intervalle
Mathématiques
Loi de probabilité à densité et loi uniforme sur un intervalle
Mathématiques
Loi normale
Mathématiques
Savoir utiliser la calculatrice pour représenter une loi normale centrée réduite
Mathématiques
Savoir utiliser la calculatrice pour représenter une loi normale
Fermer
Accédez gratuitement à
