Système de numérotation binaire
- Fiche de cours
- Quiz
- Profs en ligne
- Videos
- Application mobile
De nombreux dispositifs industriels n'utilisent que les chiffres 0 et 1 pour représenter les grandeurs physiques.
Généralement, dans de tels dispositifs, le chiffre 1 peut signifier :
- un niveau de haute pression,
- de haute tension,
- ou encore un contact fermé.
Quant au chiffre 0, il sert à désigner:
- une basse pression,
- une basse tension,
- ou un contact ouvert.
C'est pourquoi, pour pouvoir communiquer avec ces dispositifs, il faut utiliser un système de numérotation composé uniquement des chiffres 0 et 1.
Cette étude vous permettra :
- de comprendrele système de numérotation binaire (0 et 1),
- de maîtriser la conversion des nombres à partir du système conventionnel (système décimal) et vice-versa,
- et d'étudiez l'addition et la soustraction dans ce système de numérotation.
Le système de numérotation binaire est constitué de deux chiffres, 0 et 1, d'où l'origine du mot binaire. Ainsi, une colonne d'un nombre binaire ne contient que les chiffres 0 ou 1.
Par définition, tout chiffre d'un nombre binaire est appelé bit, qui est une abréviation des mots anglais binary digit.
Le nombre binaire est par conséquent appelé mot de bits.
Pour les distinguer des nombres décimaux, chaque mot de bits est placé entre parenthèses avec le chiffre 2 comme indice.
Par ailleurs, il faut lire la séquence des 1 et 0 à partir de la gauche vers la droite.
- Par exemple, le mot binaire 10001 s'écrit : (10001)2
- sa prononciation est : "un, zéro, zéro, zéro, un" et non pas "dix mille et un" comme si c'était en base 10.
Les nombres fractionnaires seront, eux aussi, notés selon le même principe que dans la base 10. Dans le système binaire, une virgule dite binaire sera introduite pour séparer la partie entière de la partie fractionnelle d'un mot de bits.
Dans un nombre binaire, le poids de chaque bit est déterminé par son rang ou son numéro.
Par définition :
- le premier bit à gauche de la virgule binaire aura le rang 0, celui à sa gauche le rang 1, et ainsi de suite.
- Le premier bit à droite de la virgule porte le rang - 1, celui à sa droite - 2, etc.
La figure suivante présente un nombre binaire fractionnaire dont la partie entière comprend 7 bits alors que sa partie fractionnelle est composée de 5 bits. Les rangs sont indiqués sous chaque bit.
Remarquez que dans la partie entière les rangs vont de 0 à 6 alors que pour la partie fractionnelle, ils vont de -1 à -5.
Représentation d'un nombre binaire :
Le poids de chaque bit est égal à 2 avec comme exposant leur rang. Une fois que les rangs ont été inscrits, les poids s'expriment selon la puissance du rang.
L'équivalent décimal d'un nombre binaire est déterminé de la manière suivante :
- Chaque bit est multiplié par son poids relatif.
- Tous les produits partiels (résultats de la multiplication de chaque bit par son poids) sont ensuite additionnés un à un.
- La somme totale représente l'équivalent décimal du nombre binaire.
Les deux exemples suivants vous permettront de maîtriser cette méthode.
Premier exemple : conversion d'un nombre binaire entier.
La figure suivante vous montre les étapes de conversion du nombre binaire (1011101)2 en nombre décimal. Vous voyez que le poids de chaque bit a été déterminé à partir de son rang. Ainsi, le poids du bit 0 est 20 = 1.
Vous répétez la même procédure jusqu'au bit 6 dont le poids est 26 = 64. Une fois que tous les poids ont été déterminés, chaque bit est alors multiplié par son poids relatif. Tous les produits sont ensuite additionnés pour former l'équivalent décimal du nombre binaire (1011101)2.
Conversion d'un nombre binaire entier en nombre décimal :
Deuxième exemple : conversion d'un nombre binaire fractionnaire.
Dans le cas d'un nombre binaire fractionnaire, c'est-à-dire un nombre qui comporte des bits à droite de la virgule binaire, la procédure précédente s'applique d'abord à la partie entière. Elle sera ensuite appliquée à la partie fractionnelle.
Le résultat sera alors placé après la virgule décimale. La figure suivante fait voir la conversion du nombre binaire (11011,1011)2.
Cette opération est effectuée en deux étapes :
- La première permet d'obtenir l'équivalent décimal de la partie entière qui est "16 + 8 + 2 + 1 = (27)10" ;
-
dans la seconde, on effectue la
conversion de la partie fractionnelle,
- ce qui donne (1/2 + 1/23 + 1/24)= (0,5 + 0,125 + 0,0625)10 = (0,6875)10.
Conversion d'un nombre binaire fractionnel en nombre décimal :
Conversion de la partie entière :
La conversion de la partie entière d'un nombre décimal en nombre binaire consiste en des divisions successives par 2 jusqu'à ce qu'un 0 soit obtenu comme quotient avec un reste de 1.
La méthode débute par la division du nombre par 2, le reste est reporté comme le bit du poids le plus faible (bit de rang 0). Le quotient de cette division est, lui aussi, divisé par 2. Le deuxième reste représente alors le bit de rang 1.
Cette procédure est reprise de la même manière jusqu'à ce que le quotient obtenu soit 0 avec un reste de 1. L'exemple de la figure suivante présente la conversion du nombre décimal 97 en nombre binaire.
Conversion du nombre décimal 97 en nombre binaire :
- La division de 97 par 2 donne un quotient de 48 avec un reste de 1 qui sera le bit du poids le plus faible.
- Le quotient de cette première division, 48, est ensuite divisé par 2 pour donner un quotient de 24 avec un reste de 0, c'est le bit 1 (deuxième bit à gauche).
- La division de 24 par 2 donne 12 avec un reste de 0 qui sera le bit 2 et ainsi de suite.
Vous remarquez que l'avant-dernière division (3/2) donne un quotient de 1, lequel divisé par 2 donne 0 comme quotient et 1 comme reste. La conversion est alors terminée.
La conversion de la partie fractionnelle s'effectue par des multiplications successives par 2. La partie entière du résultat obtenu à chaque multiplication (1 ou 0) représente alors le bit correspondant. L'emplacement des bits s'effectue de la gauche vers la droite à partir de la virgule binaire. La partie fractionnelle est ensuite multipliée par 2 et ainsi de suite. Le processus est terminé lorsque le résultat de la multiplication est égal à 1.
La figure suivante montre la conversion du chiffre décimal (0,71875)10 en nombre binaire. Notez bien les étapes de cette conversion.
La conversion d'un nombre décimal comprenant une partie fractionnelle fait appel aux deux procédures précédentes.
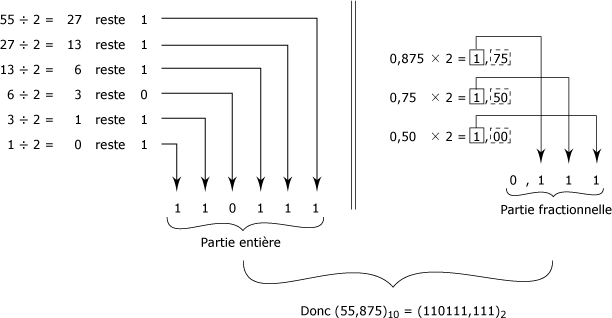
La partie entière est convertie par des divisions successives par 2 alors que l'équivalent binaire de la partie fractionnelle est obtenu par des multiplications successives par 2. La figure suivante fait voir cette méthode pour la conversion du nombre décimal (55,875)10.
Conversion d'un nombre décimal fractionnaire en nombre binaire :
L'addition dans le système binaire est basée sur un ensemble de règles qui définissent la manière d'effectuer des reports dans ce système de numérotation.
Ces règles sont les suivantes :
- Règle n° 1 : 0 + 0 = 0 ;
- Règle n° 2 : 1 + 0 = 1 ;
- Règle n° 3 : 1 + 1 = 0 avec report de 1 ;
- Règle n° 4 : 1 + 1 + 1 = 1 avec report de 1.
La figure suivante présente une bonne application de ces quatre règles. Les deux nombres à additionner sont composés de 7 bits chacun. Les reports effectués à chaque étape sont inscrits en haut du cumulande. Les rangs de chaque bit sont inscrits en bas de la somme.
Addition de deux nombres binaires :
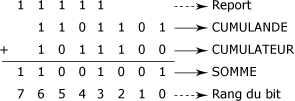
Notez bien les opérations une à une :
- bit 0 : 1 + 0 = 1 ;
- bit 1 : 0 + 0 = 0 ;
- bit 2 : 1 + 1 = 0 avec report de 1 à la colonne du bit 3 ;
- bit 3 : 1 + 1 + 1 (report) = 1 avec report de 1 à la colonne du bit 4 ;
- bit 4 : 0 + 1 + 1 (report) = 0 avec report de 1 à la colonne du bit 5 ;
- bit 5 : 1 + 0 + 1 (report) = 0 avec report de 1 à la colonne du bit 6 ;
- bit 6 : 1 + 1 + 1 (report) = 1 avec report de 1 à la colonne du bit 7 ;
- Puisque ni le cumulande ni le cumulateur n'ont des bits, le 1 reporté sera inscrit à la colonne du bit 7 de la somme.
Comme vous l'avez vu dans le cas du système décimal, la soustraction en binaire est également basée sur la notion de retenue. Cependant, dans le système binaire, il n'y a que deux chiffres dont le plus grand est 1.
Quatre règles sont alors nécessaires pour effectuer rigoureusement la soustraction en binaire :
- Règle n° 1 : 0 - 0 = 0 ;
- Règle n° 2 : 1 - 1 = 0 ;
- Règle n° 3 : 1 - 0 = 1 ;
- Règle n° 4 : 0 - 1 = 1 avec retenue.
La figure suivante présente deux exemples de soustraction dans le système binaire.
Soustraction de deux nombres binaires :
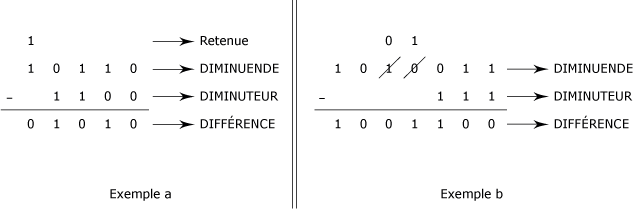
Dans l'exemple a, (1100)2 est soustrait de (10110)2.
- Colonne du bit 0 : 0 - 0 = 0 ;
- Colonne du bit 1 : 1 - 0 = 1 ;
- Colonne du bit 2 : 1 - 1 = 0 ;
- Colonne du bit 3 : 0 - 1 = 1 avec une retenue de 1.
- Cette retenue fait passer le diminuende de la colonne 4 de 1 à 0, ce qui donne 0 - 0 = 0 ;
- Le résultat final est alors (1010)2.
Dans l'exemple b, une difficulté survient à cause des retenues successives de 1 de 0. En effet, les colonnes 0 et 1 ne posent aucun problème du moment que la soustraction est à chaque fois 1 - 1 = 0. Cependant, pour la colonne du bit 2, une retenue est nécessaire pour la soustraction 0 - 1 = 1 avec une retenue de 1.Comment retenir 1 du bit 3 qui est égal à 0 ?
La solution consiste à parcourir le diminuende vers la gauche jusqu'au premier 1 (bit 4 dans ce cas), lequel sera remplacé par 0. Les 0 intermédiaires seront, quant à eux, remplacés par 1. Dans cet exemple, il y a un seul 0 intermédiaire (bit 3). On fait alors appel à une nouvelle règle de retenue qui peut être appliquée à tout système de numérotation. Son énoncé général est le suivant.
Règle de retenue de 1 de 0 :Lorsque le chiffre pour lequel il faut effectuer une retenue est 0, le diminuende est parcouru vers la gauche jusqu'au premier chiffre différent de 0. Une retenue de 1 est effectuée sur ce chiffre alors que les 0 intermédiaires sont remplacés par le plus grand chiffre du système de numérotation.
Résumé sur le système de numérotation binaire :
Après avoir parcouru cette étude, assurez-vous de retenir les points suivants :
- Le système de numérotation binaire est composé des deux chiffres 0 et 1. Chaque nombre de ce système de numérotation est composé d'une suite de ces deux chiffres.
- Un nombre binaire est appelé mot de bits alors que les chiffres (0 ou 1) sont appelés des bits.
- Par définition, la position du premier bit à gauche de la virgule binaire est la position 0. Pour les bits à sa gauche (partie entière), les positions sont croissantes à partir de 1 (1, 2, 3, 4, etc.). Pour ceux à la droite de la virgule binaire, les positions sont décroissantes de la gauche vers la droite (-1, -2, -3, -4, etc.).
- Le poids de chaque bit est égal à 2 élevé à la puissance de son poids relatif.
- L'équivalent décimal d'un nombre binaire est obtenu par l'addition des produits partiels de chaque bit par son poids relatif.
- La conversion de la partie entière d'un nombre décimal en nombre binaire s'obtient par des divisions successives par 2 jusqu'à ce qu'on obtienne 0 comme quotient avec un reste de 1.
- La conversion de la partie fractionnelle d'un nombre décimal en nombre binaire est obtenue par des multiplications successives par 2. La partie entière du résultat représente le bit correspondant (à partir de la gauche vers la droite de la virgule binaire) alors que la partie fractionnelle est de nouveau multipliée par 2. L'opération se termine lorsque le résultat d'une multiplication est égal à 1.
Vous connaissez maintenant les principes de base du système de numérotation binaire. Une étude porte sur le système de numérotation octale.
Vous avez obtenu75%de bonnes réponses !






