Lycée   >   Terminale techno   >   Mathématiques   >   Fonction logarithme décimal- Terminale- Mathématiques

Fonction logarithme décimal

  • Fiche de cours
  • Quiz
  • Profs en ligne
Objectif
  • Découvrir le logarithme décimal.
  • Connaitre le sens de variation de la fonction logarithme décimal.
  • Connaitre les propriétés algébriques de la fonction logarithme décimal et les utiliser pour transformer des expressions mathématiques.
  • Utiliser le logarithme décimal pour résoudre des équations et des inéquations.
Point clé
  • La fonction qui à tout nombre x strictement positif associe log x est appelée fonction logarithme décimal.
  • Propriétés :
  • La fonction logarithme décimal est croissante pour toute valeur strictement positive.
  • La solution de logx = a est 10a.
  • La solution de ax = b est 
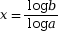
  • L'ensemble des solutions de log x  ≤  a  est  ]0 ; 10a].
  • L'ensemble des solutions de log x ≥ a  est  [10a ; +∞[.
Pour bien comprendre
  • Savoir résoudre une équation et une inéquation de degré 1.
  • Connaitre les puissances des nombres.
1. Généralités
a. Définition
La fonction qui à tout nombre x strictement positif associe log x est appelée fonction logarithme décimal.

Pour trouver des valeurs, il faudra utiliser la touche log de votre calculatrice.

Valeurs remarquables
  • log 1 = 0
  • log 10 = 1
b. Propriétés algébriques
Propriétés avec x et y sont des réels strictement positifs :
Exemple d'emploi
Sachant que log 2 ≈ 0,301, calculer log 5.
Comme 10 = 2×5 alors log 10 = log(2×5).
On sait que log 10 = 1 par définition et que log (xy) = log x + log y par propriété.
Ainsi log(2×5) = log 2 + log 5 ≈ 0,301 + log 5.
On en déduit : 1 ≈ 0,301 + log 5 et log 5 ≈  0,699.
2. Variations
Propriété
La fonction logarithme décimal est croissante pour toute valeur strictement positive.

Représentation graphique


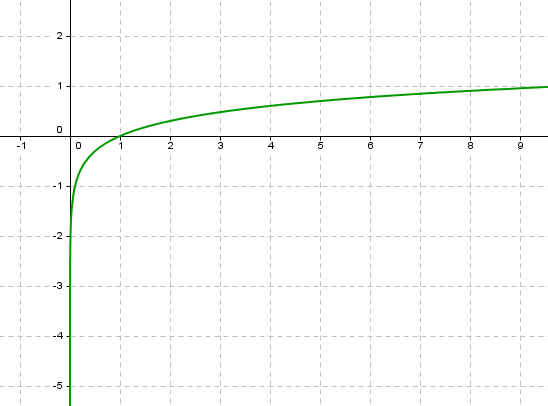
3. Résolution d'équations, d'inéquations
Propriété fondamentale due à la croissance de la fonction log :   
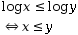
a. Résolution d'équations avec un logarithme
Propriété – Résolution de log x = a
La solution de log x = a  est 10a.
Exemple
La solution de log x = 5 est 105  = 100 000.
b. Résolution d'inéquations avec un logarithme
Propriété 1 – Résolution de log x ≤ a
On doit avoir x ≤ 10a, l'ensemble des solutions est donc : ]0 ; 10a].
Propriété 2 – Résolution de log x ≥ a
On doit avoir x ≥ 10a, l'ensemble des solutions est donc : [10a ; +∞[.
c. Résolution d'équations avec une exponentielle
Propriété – Résolution de ax = b
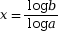
La solution de ax = b  est 
Preuve

ax= b équivaut à log ax = log b, et comme log ax=x log a, l'équation équivaut à x log a=log b  d'où . 

Exemple
L'évolution d'un capital de 2000 euros placé à 4% d'intérêt annuel en fonction du nombre n d'années est donné par la formule 20001,04n.
Au bout de combien d'années ce capital est-il doublé ? 
On cherche à résoudre 20001,04n ⩾ 4000 soit 1,04n ⩾ 2 d'où log1,04n ⩾ log2 soit nlog1,04 ⩾ log2 et enfin n ⩾ log2log1,04 car log 1,04 > 0.
On trouve n ⩾ 18. Il faut 18 ans pour doubler un capital placé à 4% d'intérêt annuel.

Comment as-tu trouvé ce cours ?

Évalue ce cours !

 

Note 3.9 / 5. Nombre de vote(s) : 32
Question 1/5

La médiane de 6 notes est 13. Cela signifie que :
Question 2/5

On a obtenu la série statistique suivante :

Combien vaut la médiane ?
Question 3/5

On a obtenu la série ci-dessous :

Quelle est la médiane de cette série ?
Question 4/5

On a relevé les tailles en cm des élèves d’une classe :

 

Parmi les propositions suivantes, laquelle est vraie ?
Question 5/5

Les notes en français de deux classes littéraires sont données dans le tableau suivant :

Quelle est la note médiane ?

Vous avez obtenu75%de bonnes réponses !

Recevez l'intégralité des bonnes réponses ainsi que les rappels de cours associés :

Votre adresse e-mail sera exclusivement utilisée pour vous envoyer notre newsletter. Vous pourrez vous désinscrire à tout moment, à travers le lien de désinscription présent dans chaque newsletter. Pour en savoir plus sur la gestion de vos données personnelles et pour exercer vos droits, vous pouvez consulter notre charte.

Une erreur s'est produite, veuillez ré-essayer

Consultez votre boite email, vous y trouverez vos résultats de quiz!

Découvrez le soutien scolaire en ligne avec myMaxicours

Le service propose une plateforme de contenus interactifs, ludiques et variés pour les élèves du CP à la Terminale. Nous proposons des univers adaptés aux tranches d'âge afin de favoriser la concentration, encourager et motiver quel que soit le niveau. Nous souhaitons que chacun se sente bien pour apprendre et progresser en toute sérénité ! 

EXERCE TOI EN T'ABONNANT

Fiches de cours les plus recherchées

Mathématiques

CanardMasqué présente : Les systèmes de numération

Mathématiques

Le vocabulaire des probabilités

Mathématiques

Utilisation du tableur pour des tableaux croisés

Mathématiques

Isoler une variable

Mathématiques

Appliquer une formule

Mathématiques

Coefficient directeur de la tangente à une courbe en un point

Mathématiques

Somme des termes d'une suite arithmétique- Terminale- Mathématiques

Mathématiques

Somme des termes d'une suite géométrique- Terminale- Mathématiques

Mathématiques

Fonctions exponentielles de base q

Mathématiques

La fonction inverse- Terminale- Mathématiques

Mathématiques

Ajustement affine