Vibrations mécaniques (2)
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Jusqu'à présent, il n'a été question que de signaux associés à un mouvement périodique, soit un mouvement qui se répète et dont chaque cycle reproduit toujours le même cycle. Un autre type de mouvement vibratoire est associé à un écoulement turbulent, à de la cavitation, au frottement, aux chocs successifs d'une pièce perdue dans une machine, etc. Tous ces phénomènes sont de nature aléatoire.Il en est de même des vibrations qu'ils génèrent, nommées vibrations aléatoires.
Une vibration aléatoire, contrairement à une vibration périodique, consiste en un mouvement irrégulier dont l'amplitude en fonction du temps ne se répète jamais d'une façon identique.
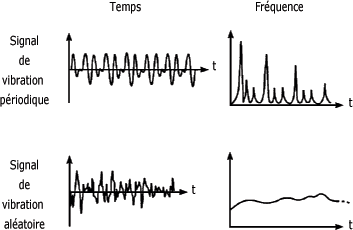
Ici, il n'est pas possible d'identifier une ou des fréquences permettant à coup sûr la reconnaissance du problème, comme c'est le cas dans le spectre de fréquences (figure suivante). Une vibration aléatoire n'a pas de période ni d'harmoniques, comme le montre la deuxième figure.
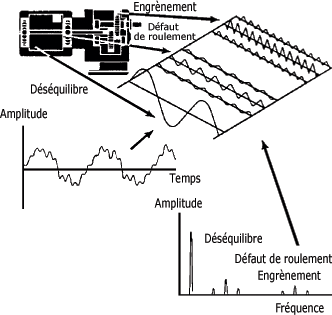
Vibration d'une machine en fonction du temps et de la fréquence :
Vibration périodique et vibration aléatoire :
La vibration d'une machine soumise à une force périodique, comme un déséquilibre, peut être décrite en termes de déplacement (déjà vu), de vitesse ou d'accélération.
La vitesse du mouvement vibratoire correspond à la variation de son déplacement pour une unité de temps. L'accélération représente une variation de la vitesse par unité de temps.
Examinez de près la figure ci-dessous. Elle permet de mieux visualiser l'évolution de ces trois paramètres au cours d'une période complète de la vibration harmonique simple d'un système "masse-ressort".
Le tableau au-dessous de la courbe indique l'amplitude de chaque paramètre en fonction du temps, représenté ici en fraction de période T.
Relation entre d, v, a :
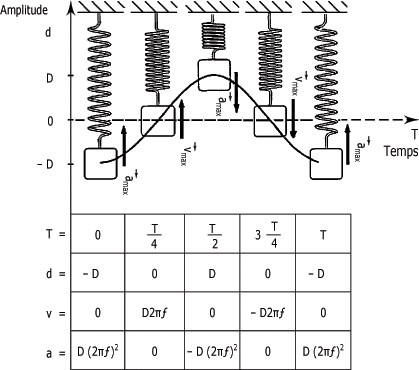
La période de vibration est la même pour les trois paramètres. La différence essentielle réside dans un déphasage de 90° entre le déplacement (d) et la vitesse (v), et de 180° entre le déplacement et l'accélération (a).
Les amplitudes des trois paramètres sont reliées mathématiquement en fonction de la fréquence du signal. Le tableau de la figure ci-dessus montre que l'amplitude de la vitesse est obtenue en multipliant celle du déplacement par un facteur proportionnel à la fréquence.
De même que l'amplitude de l'accélération s'obtient en multipliant celle du déplacement par un signal proportionnel au carré de la fréquence.
Il existe plusieurs façons de mesurer l'amplitude de la vibration. La figure suivante représente la forme la plus simple de l'évolution d'une vibration dans le temps. L'amplitude mentionnée peut être le déplacement, la vitesse ou l'accélération.
Mesure de l'amplitude d'une vibration harmonique simple :
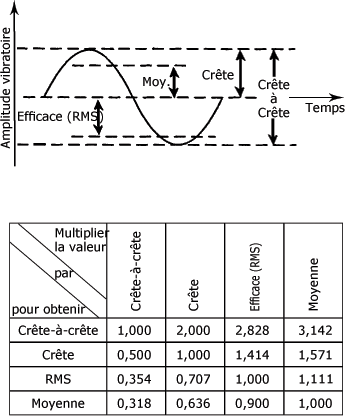
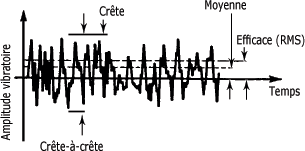
La valeur de crête-à-crête indique la différence entre les amplitudes maximale et minimale du mouvement. C'est une quantité utile pour déterminer le déplacement d'un composant, déplacement qui peut être critique pour des considérations de contrainte maximale ou de jeu mécanique.
La valeur de crête donne l'amplitude maximale et s'avère utile dans les mesures concernant les phénomènes de courte durée ; les chocs en sont un exemple.
Cependant, elle ne tient pas compte de l'évolution de la vibration dans le temps.
La valeur moyenne tient compte de cette évolution mais, contrairement à la valeur efficace, n'a aucune relation avec une grandeur physique quelconque.
Valeur efficace =
.
La valeur efficace ou valeur moyenne quadratique (RMS - Root Mean Square) est la mesure la plus intéressante des amplitudes de vibration. En plus de tenir compte de l'évolution du signal dans le temps, le calcul de la valeur efficace est lié à l'énergie vibratoire et donc au "potentiel de détérioration" de la vibration.
Valeur moyenne =
.
En pratique, le détecteur de valeur efficace élève au carré les valeurs instantanées positives et négatives dès leur apparition. Il effectue ensuite une moyenne sur une certaine période de temps, puis extrait la racine carrée du résultat. La valeur efficace d'un mouvement sinusoïdal est égale à environ 0,7 fois la valeur de crête de l'amplitude du signal.
Le facteur de crête définit le rapport de la valeur de crête d'un signal à sa valeur efficace. D'après la définition du niveau efficace, le facteur de crête du mouvement sinusoïdal est environ 1,4. Plus la vibration devient impulsive, plus la valeur de crête augmente.
Les amplitudes vibratoires que vous venez d'apprendre ne servent pas seulement à décrire un signal sinusoïdal simple. Elles sont aussi employées dans le cas d'un signal complexe tel que celui montré à la figure suivante.
Mesure de l'amplitude d'une vibration périodique :
Dans la terminologie des vibrations, on utilise quelquefois le terme "niveau" pour signifier une amplitude. Cet usage est déconseillé. Le niveau définit plutôt le rapport d'une valeur quelconque à une valeur de référence.
Par exemple, lors d'une inondation, le niveau de l'eau dans un sous-sol a grimpé jusqu'à 50 cm. Cela signifie que la hauteur de l'eau par rapport à la hauteur du plancher est de 50 cm.
Le niveau de vibration est défini comme le rapport logarithmique d'une amplitude mesurée (Xmes.) à une amplitude de référence (Xréf.).
Les unités de mesure du SI pour l'accélération, la vitesse et le déplacement sont respectivement:
- le mètre par seconde carrée (m/s2),
- le mètre par seconde (m/s) et,
- le mètre (m).
Toutefois, les deux dernières quantités sont de trop grande dimension pour quantifier les amplitudes de vitesse et de déplacement obtenues par la mesure des vibrations sur les machines industrielles. Les unités usuelles sont plutôt le millimètre par seconde (mm/s) et le micromètre (µm).
Le tableau récapitulatif présenté à la figure ci-dessous vous montre les relations qui existent entre les unités les plus couramment utilisées dans la mesure des vibrations.
Unités de mesure :

L'accélération de la pesanteur g est largement utilisée pour quantifier l'amplitude des mesures faites en accélération. Les unités m/s2 et g sont reliées par un facteur d'environ 10, ce qui rend la conversion de l'un à l'autre plutôt simple.
Il vous reste un dernier point à voir pour compléter votre initiation aux vibrations mécaniques : la représentation graphique des signaux vibratoires dans le domaine des fréquences.
Oubliez pour un instant les vibrations. Considérez plutôt la situation montrée à la figure suivante. Il peut être difficile de juger de la quantité d'essence qui reste dans un réservoir. Si la jauge avait une échelle logarithmique, l'extrémité gauche de l'échelle serait "étirée". Vous obtiendriez une meilleure lecture pour les bas niveaux.
Jauge avec des échelles linéaire et logarithmique :
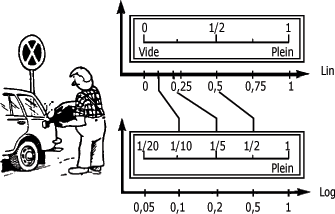
Vous aurez noté que l'échelle logarithmique ne commence pas à zéro. De même que les distances sur la jauge entre les positions 0,1 et 1 et les positions 0,05 et 0,5 sont égales.
Le choix de l'échelle dépend de l'unité à dimensionner. La distance et le temps sont des exemples d'échelles linéaires. Toutefois, pour dimensionner des unités où le rapport entre deux valeurs est plus intéressant à connaître que leur valeur absolue, il peut être avantageux d'utiliser une échelle logarithmique.
Les différentes pièces de monnaie et les billets de banque d'un système monétaire offrent l'exemple d'un cas concret. Ils ont souvent des valeurs qui, lorsque positionnées sur une échelle logarithmique, montrent un écart approximativement égal entre deux valeurs adjacentes (figure suivante). Vous remarquerez aussi que dans une décade il existe un rapport de 10 entre les limites inférieure et supérieure de l'échelle.
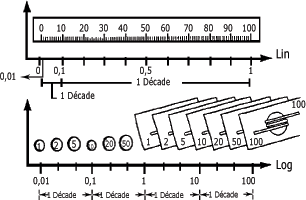
En vibration, tant les échelles de fréquence linéaire que logarithmique sont utilisées, chacune ayant ses avantages.
Une échelle logarithmique est mieux adaptée à la détection et à la prévision des défauts. Elle a pour effet d'élargir les gammes de basse fréquence et de comprimer les gammes de haute fréquence. Il en résulte un spectre qui donne une image complète de la vibration sans pour autant compromettre la résolution en basse fréquence.
La figure suivante vous montre la représentation du même signal vibratoire sur une échelle linéaire et une échelle logarithmique. Notez dans les deux cas quelle portion de l'échelle est consacrée aux fréquences inférieures à 200 Hz.
Signal vibratoire représenté sur des échelles de fréquence linéaire et logarithmique :
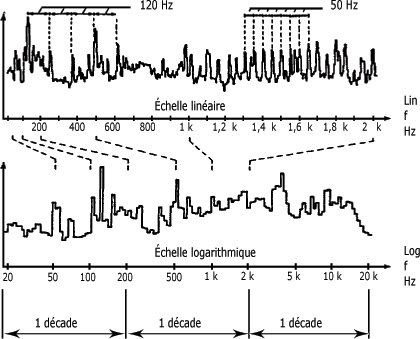
Échelles d'amplitude linéaire et logarithmique :
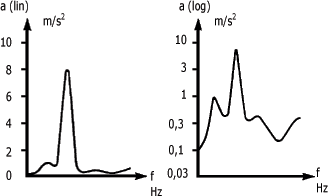
L'échelle logarithmique peut être étalonnée en unités physiques (m/s2, mm/s, µm), mais les décibels sont aussi utilisés. Le décibel, noté dB, est une unité de mesure du niveau donné par la relation suivante :
dB = 20 log (Xmes./Xréf.);
ex. : Xréf. = 1, Xmes. = 100 et dB = 20 log (100/1) = 40 dB.
Toute grandeur peut être mesurée en décibel. Les valeurs de référence sont parfois normalisées. C'est le cas pour les rapports d'amplitudes vibratoires. D'après la norme ISO 1683, les amplitudes de référence sont :
o accélération : aréf. = 10-6 m/s2 ;
o vitesse : vréf. = 10-9 m/s ou 10-6 mm/s ;
o déplacement : dréf. = 10-12 m ou 10-6 µm.
Le grand avantage d'une échelle en dB est qu'elle permet de conserver des valeurs numériques de grandeur raisonnable. La figure 1.32 vous montre l'échelle de conversion du niveau de vitesse vibratoire - dB (réf. 10-6 mm/s) en unités absolues de vitesse (mm/s).
Échelle de conversion dB - mm/s :
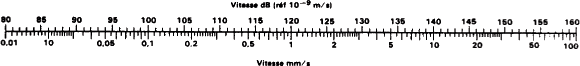
La vibration est un monde dans lequel une connaissance adéquate du vocabulaire utilisé s'avère essentielle. Avant de poursuivre votre apprentissage, assurez-vous de bien comprendre la terminologie suivante.
o Un mouvement périodique est un mouvement qui se répète et dont chaque cycle est identique au précédent.
o La période est la durée d'un cycle.
o Un mouvement oscillatoire est un mouvement périodique de va-et-vient d'un objet autour d'une position d'équilibre.
o La vibration est le phénomène dynamique associé au mouvement oscillatoire d'un système mécanique.
o Une vibration sinusoïdale correspond à un mouvement oscillatoire qui varie sinusoïdalement en fonction du temps.
o L'amplitude est la valeur maximale de la vibration sinusoïdale.
o La fréquence est l'inverse de la période.
o La phase est la position d'une pièce en vibration en référence à un point fixe ou à une autre pièce en vibration.
o Le déphasage est la différence de phase entre deux vibrations sinusoïdales.
o La fréquence naturelle est la fréquence d'un système en vibration qui oscille librement sans aucune contrainte.
o La vibration amortie est une vibration dont l'amplitude diminue avec le temps.
o La vibration forcée est une vibration entretenue par une force externe.
o La résonance est le phénomène associé à l'augmentation de l'amplitude d'une vibration dont la fréquence d'excitation coïncide avec une fréquence naturelle.
o La fréquence de résonance est la fréquence à laquelle une résonance se produit.
o Une vibration périodique correspond à un mouvement périodique qui peut être décomposé en une somme infinie de mouvements sinusoïdaux.
o La fréquence fondamentale est la fréquence la plus basse d'une vibration périodique.
o Un harmonique est le multiple entier d'une fréquence fondamentale.
o L'analyse en fréquence est la technique qui permet la décomposition d'un signal vibratoire périodique en composantes sinusoïdales ou fréquentielles.
o Le spectre de fréquence est la représentation du signal vibratoire où l'amplitude est affichée en fonction de la fréquence.
o Les vibrations aléatoires correspondent à un mouvement de nature aléatoire, c'est-à-dire qui n'a pas de période ni d'harmoniques.
o Les paramètres de vibration permettent de décrire la vibration de tout système mécanique en termes de déplacement, de vitesse ou d'accélération.
o La valeur de crête est la valeur maximale d'une vibration.
o La valeur de crête-à-crête est la différence entre les écarts extrêmes d'une vibration.
o La valeur efficace est la valeur moyenne quadratique (RMS).
o Le niveau de vibration est le rapport logarithmique d'une valeur mesurée à une valeur de référence.
o L'échelle linéaire est employée en vibration lorsqu'une haute résolution est requise.
o L'échelle logarithmique est employée en vibration lorsque l'affichage des mesures sur une large gamme d'amplitudes ou de fréquences est requise.
o Le décibel (dB) est l'unité de mesure du niveau de vibration.
Vous connaissez maintenant en quoi consiste une description précise des vibrations en un point sur une machine.

Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.

Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.

Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.

Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !

Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.

Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !







