Variations de fonctions polynômes
- Fiche de cours
- Quiz
- Profs en ligne
- Videos
- Application mobile
Sommaire : Méthode – Exemple
d’une fonction polynôme de degré 2
– de degré 3
1. Méthode
Pour étudier le sens de variation d’une fonction
f dérivable sur un intervalle [a ;
b], il faut :
1. Calculer sa dérivée f ’(x).
2. Déterminer le signe de f ’(x) sur [a ; b] ; appliquer le théorème suivant :
• lorsque la fonction dérivée f ’ est positive sur un intervalle I, la fonction f
est croissante sur I ;
• lorsque la fonction dérivée f ’ est négative sur I, la fonction f
est décroissante sur I ;
• lorsque la fonction dérivée f ’ est nulle sur I, la fonction f
est constante sur I.
3. Dresser le tableau de variation de f.
1. Calculer sa dérivée f ’(x).
2. Déterminer le signe de f ’(x) sur [a ; b] ; appliquer le théorème suivant :
• lorsque la fonction dérivée f ’ est positive sur un intervalle I, la fonction f
est croissante sur I ;
• lorsque la fonction dérivée f ’ est négative sur I, la fonction f
est décroissante sur I ;
• lorsque la fonction dérivée f ’ est nulle sur I, la fonction f
est constante sur I.
3. Dresser le tableau de variation de f.
2. Variations d’une fonction polynôme de degré
2
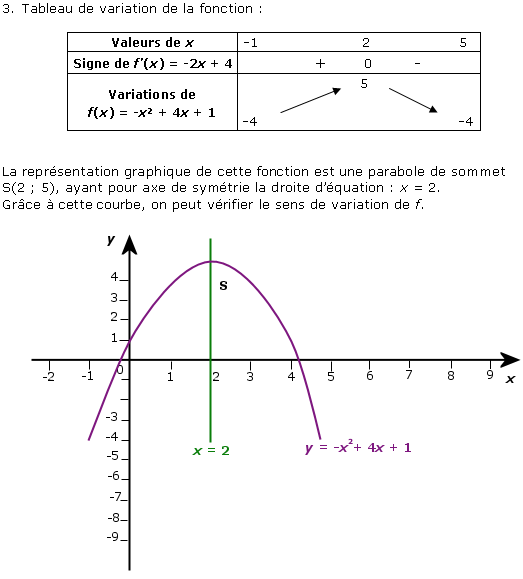
Soit f la fonction définie sur [-1 ;
5] par f(x) = -x² + 4x +
1.
Etudions les variations de cette fonction sur [-1 ; 5].
1. Calcul de la dérivée : f ’(x) = -2x + 4.
2. Signe de la dérivée :
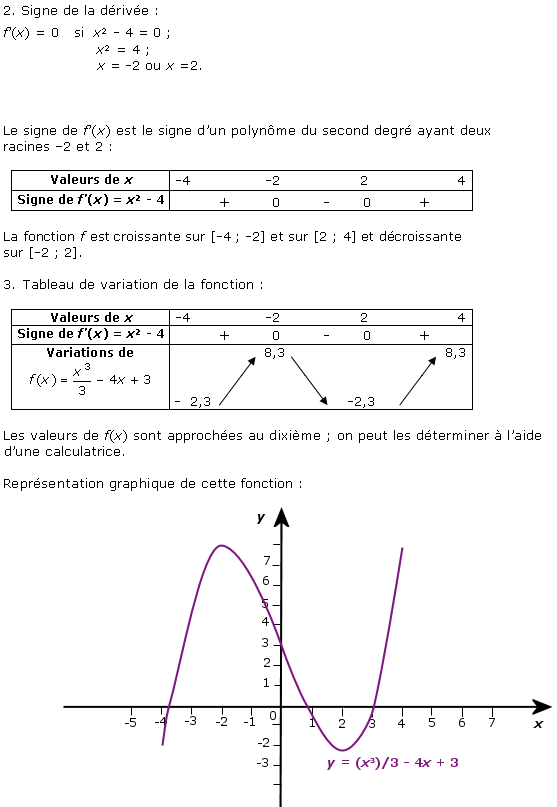
3. Variations d’une fonction polynôme de degré
3
Comment as-tu trouvé ce cours ?
Évalue ce cours !
Vous avez obtenu75%de bonnes réponses !
Recevez l'intégralité des bonnes réponses ainsi que les rappels de cours associés :
Fermer
Accédez gratuitement à
