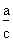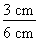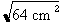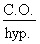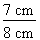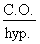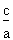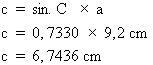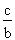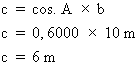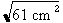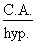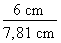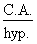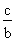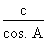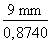Trigonométrie appliquée aux triangles rectangles (1)
- Fiche de cours
- Quiz et exercices
- Vidéos et podcasts
Le calcul de la mesure d'un côté ou d'un angle d'un triangle à l'aide de la trigonométrie s'effectue différemment selon qu'il s'agit d'un triangle rectangle ou d'un triangle quelconque.
Il s'avère donc essentiel de distinguer les définitions trigonométriques qui s'appliquent à chacune de ces catégories de triangles.
Dans cette étude, vous étudierez :
- les fonctions trigonométriques qui s'appliquent aux triangles rectangles ;
- le sinus ;
- le cosinus ;
- la tangente.
Il existe trois fonctions trigonométriques de base :
- le sinus ;
- le cosinus ;
- la tangente.
Dans le cas des triangles rectangles, ces fonctions établissent différents rapports entre les côtés d'un même triangle : le côté opposé à un angle, le côté adjacent à un angle et l'hypoténuse.
Ces trois côtés sont désignés par des abréviations :
- côté opposé : C.O. ;
- côté adjacent : C.A. ;
- hypoténuse : hyp.
La figure suivante identifie ces trois côtés du triangle rectangle:
- Le côté opposé à un angle est le côté lui faisant face ;le côté opposé à l'angle A est donc le côté a;
- Le côté adjacent à l'angle A est le côté c;
- la lettre b identifie l'hypoténuse de ce triangle.
Identification des côtés d'un triangle rectangle :
Puisque les fonctions trigonométriques expriment des rapports de grandeurs entre les côtés d'un triangle, elles s'expriment en valeur absolue, c'est-à-dire sans unité de mesure.
Le Sinus :
La fonction sinus (sin.) représente le rapport entre la mesure du côté opposé à l'angle de référence et la mesure de l'hypoténuse d'un triangle rectangle.
La relation mathématique définissant le sinus s'exprime comme suit :
sin. =
.
Sinus :
L'exemple suivant vous permettra de vous familiariser avec les applications de la fonction sinus.
|
Problème
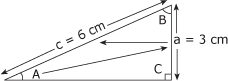
Calculez la valeur décimale (naturelle) du sinus de l'angle A du triangle de la figure 4.3. Figure 4.3 Triangle 1.
1. Identification des données La figure 4.3 indique que le côté opposé à l'angle A mesure 3 cm, tandis que l'hypoténuse mesure 6 cm. 2. Calcul du sinus Pour connaître la valeur du sinus de l'angle A, il suffit d'appliquer la formule de calcul du sinus :
La valeur décimale du sinus de l'angle A est donc 0,5. |
Le Sinus : problème 1
|
Problème
1:
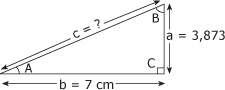
Calculez la valeur du sinus de l'angle B du triangle de la figure 4.4. Figure 4.4 Triangle 2.
1. Identification des données La figure 4.4 indique les données suivantes : - sin. B = ? - C.O. = b = 7 cm - hyp. = c = ? - a = 3,873 cm Pour pouvoir calculer la valeur du sinus de l'angle B, il nous faut d'abord connaître la valeur de l'hypoténuse du triangle. 2. Calcul de la valeur de l'hypoténuse Pour trouver la valeur de l'hypoténuse, appliquons l'équation du théorème de Pythagore : c2 = a2 + b2 c2 = (3,873 cm)2 + (7 cm)2 c2 = 15 cm2 + 49 cm2
c = c = 8 cm L'hypoténuse mesure 8 cm. 3. Calcul du sinus Il ne reste plus qu'à appliquer la formule de calcul du sinus :
sin. B =
sin. B =
sin. B = sin. B = 0,8750 La valeur décimale du sinus de l'angle B est 0,8750. |
Le Sinus : problème 2
|
Problème
2:
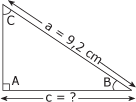
Le sinus de l'angle A du triangle de la figure 4.5 est égal à 0,7330. Calculez la longueur du côté c. Figure 4.5 Triangle 3.
1. Identification des données D'après l'énoncé du problème, nous savons que le sinus de l'angle A vaut 0,7330. La figure 4.5 indique que l'hypoténuse du triangle mesure 9,2 cm. 2. Calcul de la valeur du côté c Pour calculer la valeur du côté c, nous devons employer la formule de calcul du sinus et la modifier de façon à isoler le côté c. Nous avons donc :
qui devient : Le côté c mesure 6,7436 cm. |
Le Cosinus :
La fonction cosinus (cos.) établit le rapport entre la mesure du côté adjacent à l'angle de référence et la valeur de l'hypoténuse d'un triangle rectangle.
La formule mathématique permettant de trouver le cosinus d'un angle s'écrit donc comme suit :
cos. A =
.
Afin d'être en mesure d'effectuer les calculs relatifs à la fonction cosinus, étudiez attentivement les exemples suivants.
|
Problème
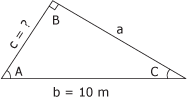
La valeur naturelle du cosinus de l'angle A du triangle de la figure 4.10 est égale à 0,6000. Calculez la valeur du côté c. Figure 4.10 Triangle 7.
1. Identification des données L'énoncé du problème nous apprend que le cosinus de l'angle A vaut 0,6000. La figure 4.10 indique que l'hypoténuse mesure 10 m. 2. Calcul de la valeur du côté c Pour trouver la valeur du côté c, il suffit d'appliquer la formule de calcul du cosinus, en la transformant pour isoler le côté c :
cos. A =
cos. A = devient :
Le côté c mesure 6 m. |
Le Cosinus: problème 1
|
Problème
1:
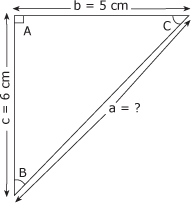
Calculez la valeur du cosinus de l'angle B du triangle de la figure 4.11. Figure 4.11 Triangle 8.
1. Identification des données La figure 4.11 nous permet d'établir les données suivantes : - cos. B = ? - C.A. = c = 6 cm - C.O. = b = 5 cm - hyp. = a = ? Pour résoudre le problème, nous devons déterminer la valeur de l'hypoténuse en appliquant le théorème de Pythagore. 2. Calcul de la valeur de l'hypoténuse Le théorème de Pythagore nous permet d'écrire que : a2 = b2 + c2 a2 = (5 cm2) + (6 cm2)
a2 = a2 = 7,81 cm 3. Calcul du cosinus Il ne reste plus qu'à appliquer la formule de calcul du cosinus :
cos. B =
cos. B = cos. B = 0,7682 Le cosinus de l'angle B vaut 0,7682. |
Le Cosinus: problème 2
|
Problème 2:
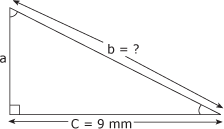
La valeur décimale du cosinus de l'angle A du triangle de la figure 4.12 égale 0,8740. Calculez la valeur de l'hypoténuse. Figure 4.12 Triangle 9.
1. Identification des données A partir de l'énoncé du problème et de la figure 4.12, nous pouvons établir que : - cos. A = 0,8740 - C.A. = c = 9 mm - hyp. = b = ? 2. Calcul de la valeur de l'hypoténuse Transformons la formule de calcul du cosinus en isolant l'hypoténuse :
cos. A =
cos. A = devient :
b =
b = b = 10,297 L'hypoténuse mesure 10,297 mm. |
La fonction tangente (tg) représente le rapport entre la mesure du côté opposé à l'angle de référence et la mesure de son côté adjacent.
On peut aussi définir la fonction tangente comme le rapport entre le sinus et le cosinus d'un angle.
On peut donc exprimer la fonction tangente à l'aide de l'une ou l'autre des relations mathématiques suivantes :
tg =
ou tg =
.
Tangente :
Il arrive qu'on utilise l'abréviation tan pour désigner la tangente.
Évalue ce cours !
Des quiz et exercices pour mieux assimiler sa leçon
La plateforme de soutien scolaire en ligne myMaxicours propose des quiz et exercices en accompagnement de chaque fiche de cours. Les exercices permettent de vérifier si la leçon est bien comprise ou s’il reste encore des notions à revoir.
Des exercices variés pour ne pas s’ennuyer
Les exercices se déclinent sous toutes leurs formes sur myMaxicours ! Selon la matière et la classe étudiées, retrouvez des dictées, des mots à relier ou encore des phrases à compléter, mais aussi des textes à trous et bien d’autres formats !
Dans les classes de primaire, l’accent est mis sur des exercices illustrés très ludiques pour motiver les plus jeunes.
Des quiz pour une évaluation en direct
Les quiz et exercices permettent d’avoir un retour immédiat sur la bonne compréhension du cours. Une fois toutes les réponses communiquées, le résultat s’affiche à l’écran et permet à l’élève de se situer immédiatement.
myMaxicours offre des solutions efficaces de révision grâce aux fiches de cours et aux exercices associés. L’élève se rassure pour le prochain examen en testant ses connaissances au préalable.
Des vidéos et des podcasts pour apprendre différemment
Certains élèves ont une mémoire visuelle quand d’autres ont plutôt une mémoire auditive. myMaxicours s’adapte à tous les enfants et adolescents pour leur proposer un apprentissage serein et efficace.
Découvrez de nombreuses vidéos et podcasts en complément des fiches de cours et des exercices pour une année scolaire au top !
Des podcasts pour les révisions
La plateforme de soutien scolaire en ligne myMaxicours propose des podcasts de révision pour toutes les classes à examen : troisième, première et terminale.
Les ados peuvent écouter les différents cours afin de mieux les mémoriser en préparation de leurs examens. Des fiches de cours de différentes matières sont disponibles en podcasts ainsi qu’une préparation au grand oral avec de nombreux conseils pratiques.
Des vidéos de cours pour comprendre en image
Des vidéos de cours illustrent les notions principales à retenir et complètent les fiches de cours. De quoi réviser sa prochaine évaluation ou son prochain examen en toute confiance !
Fermer
Accédez gratuitement à
