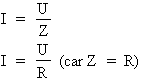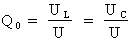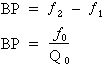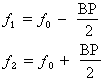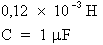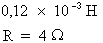Impédance circuit RLC en série (3)
- Fiche de cours
- Quiz
- Profs en ligne
- Videos
- Application mobile
Vous avez appris jusqu'à maintenant qu'un circuit RLC en série peut être surtout inductif ou surtout capacitif selon le rapport de grandeur entre la réactance inductive et la réactance capacitive.
Toutefois, lorsque la valeur de la réactance inductive est égale à celle de la réactance capacitive (XL = XC), le circuit n'est ni surtout inductif ni surtout capacitif. Il s'agit là d'un phénomène tout particulier appelé résonance.
Un circuit RLC en série est dit en résonance lorsque les effets des réactances s'annulent, c'est-à-dire lorsque : XL = XC
L'impédance du circuit est alors à son minimum et est simplement égale à la résistance du circuit (Z = R).
Dans : 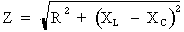
Si : XL = XC alors : Z = R
Étant donné que le courant est partout le même dans un circuit en série et comme les réactances sont égales (XL = XC), les tensions aux bornes des composants L et C sont égales et s'annulent.
Par conséquent, la tension appliquée au circuit est égale à la tension aux bornes de la résistance. La figure suivante représente la relation de phase entre les tensions et le courant dans un circuit RLC en résonance.
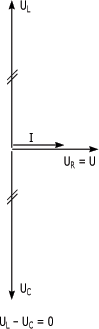
Lorsque XL = XC, le courant du circuit est en phase avec la tension appliquée au circuit. Il peut être calculé par l'une des formules suivantes :
Où :
I : courant du circuit en ampères (A)
U : tension appliquée au circuit en volts (V)
Z : impédance du circuit en ohms
R : résistance du circuit en ohms
Puisque l'impédance d'un circuit RLC en résonance est à son minimum, le courant du circuit est à son maximum.
De ce fait, la tension aux bornes du condensateur et celle aux bornes de la bobine sont également à leur maximum.
C'est pourquoi lors de la prise des mesures d'un circuit RLC en résonance, il est nécessaire de prendre toutes les précautions qui s'imposent.
Lors de la résonance:
- l'impédance d'un circuit RLC en série est à son minimum;
- et le courant du circuit à son maximum.
Alors, quelles sont les valeurs de l'impédance et du courant à proximité de la résonance ? Cette question trouvera sa réponse dans les courbes de résonance présentées ci-dessous.
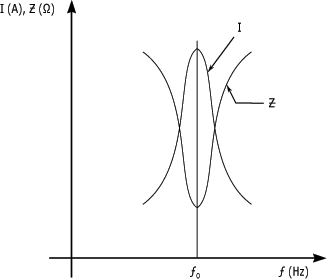
La figure représente respectivement le courant et l'impédance d'un circuit RLC en série en fonction de la fréquence.
On peut voir qu'à la fréquence de résonance, l'impédance est à sa valeur minimale. On remarque également qu'elle augmente symétriquement par rapport à la fréquence de résonance (f0) au fur et à mesure que la fréquence du circuit s'éloigne de sa valeur de résonance (f0).
Par contre, à la fréquence de résonance, le courant est à son maximum et sa valeur diminue graduellement de façon symétrique au voisinage de la fréquence de résonance.

Il est également possible d'obtenir les courbes
de résonance pour les tensions UR, UL et UC. Ces courbes, en effet,
seront semblables à celles du courant, puisque ces tensions
sont toutes des produits du courant.
Il est important de dire que la
fréquence de résonance d'un circuit RLC en
série est déterminée par le produit de
l'inductance et de la capacité (LC) via l'équation :
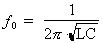
Pour une fréquence de résonance donnée, différentes valeurs de L et de C peuvent donner le même produit (LC), pour autant que la condition de résonance soit respectée, c'est-à-dire que XL = XC.
Le tableau ci-dessous vous fait voir quelques exemples de combinaisons de L et de C à une fréquence de résonance de 4 000 Hz.
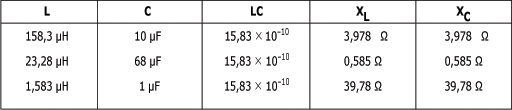
Ce tableau vous montre que lors de la résonance, les réactances peuvent être différentes malgré une fréquence de résonance identique, soit 4 000 Hz. C'est pourquoi lors de la résonance, un circuit RLC en série peut être caractérisé par un facteur de qualité "Q0". Ce facteur est défini par le rapport entre la réactance inductive ou capacitive et la résistance, comme le montrent les formules suivantes :
ou
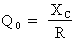
Où :
XL = XC : réactance à la résonance en ohms
R : résistance du circuit en ohms
Q0 : facteur de qualité du circuit (sans unité)
Lors de la résonance d'un
circuit RLC en série, la chute de tension aux bornes
de la résistance est toujours égale à celle
appliquée au circuit (UR = U).
Cependant, la tension aux bornes de la bobine (UL) est égale à celle
aux bornes du condensateur (UC), et elles ne sont pas
nécessairement égales à la tension appliquée
au circuit. En effet, la relation entre ces tensions
s'exprime mathématiquement comme suit :
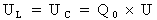
Où :
UL : tension aux bornes de la bobine à la résonance du circuit en volts (V)
UC : tension aux bornes du condensateur à la résonance du circuit en volts (V)
U : tension appliquée au circuit en volts (V)
Q0 : facteur de qualité (sans unité)
On appelle également le facteur de qualité "Q0" coefficient de surtension, puisque effectivement il correspond au rapport de la tension maximale, soit du condensateur ou de la bobine lors de la résonance, et la tension appliquée au circuit.
Dans beaucoup de circuits électroniques, il est parfois nécessaire d'éliminer des courants de certaines fréquences et de laisser passer des courants d'autres fréquences.
De là découle une des applications du circuit RLC en série qui est en résonance, à savoir son utilisation comme filtre passe-bande.
Lors de la résonance d'un circuit RLC en série :
- le courant du circuit,
- la chute de tension aux bornes de chacun des composants, UR, UL et UC, sont à leur maximum.
Cependant, ils diminueront au fur et à mesure que la fréquence du circuit s'éloignera de sa valeur de résonance.
La figure suivante représente la tension aux bornes de la résistance en fonction de la fréquence.
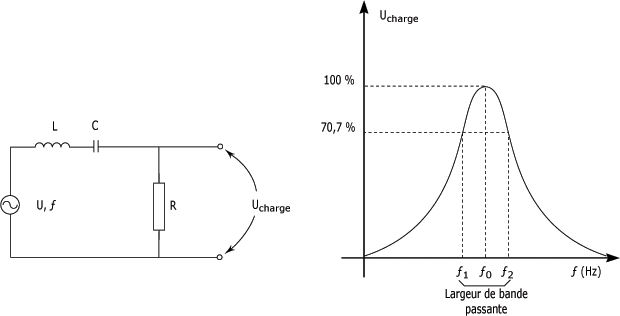
Ce circuit peut être utilisé comme un filtre passe-bande, dans lequel la bande passante est limitée par les fréquences où la tension tombe à 70,7 % de sa valeur maximale.
La largeur de cette bande passante peut être calculée par l'une ou l'autre des formules suivantes :
Où :
BP : largeur de la bande passante en hertz (Hz)
f2 : fréquence de coupure supérieure en hertz (Hz)
f1 : fréquence de coupure inférieure en hertz (Hz)
f0 : fréquence de résonance en hertz (Hz)
Q0 : facteur de qualité du circuit (sans unité)
Étant donné que la courbe de résonance est symétrique par rapport à la fréquence de résonance, il est permis de dire que chacune des fréquences de coupure inférieure et supérieure a, à partir de la fréquence de résonance, une distance correspondant à la moitié de la bande passante. Cet énoncé peut être exprimé mathématiquement par les équations suivantes :
Problème :
Le circuit de la figure suivante présente les données suivantes :
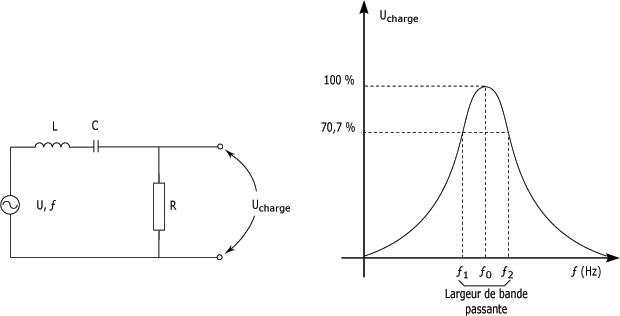
R = 4 Ohms,
L = 120 mH
et C = 1 µF
1. Calculez la
fréquence de résonance de ce
circuit.
2. Calculez la largeur de la bande
passante de ce filtre.
3. Calculez pour ce
filtre :
a) la
fréquence de coupure
inférieure ;
b) la fréquence de coupure
supérieure.
Solution :
1. Calcul de la fréquence de résonance :
Formule : 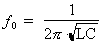 où :
Pi = 3,14 et
L = 120 mH
où :
Pi = 3,14 et
L = 120 mH
Ou :
Ou : 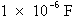
Donc : 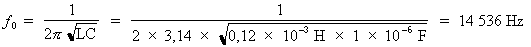
La fréquence de résonance du circuit est égale à 14 536 Hz.
2. Calcul de la largeur de la bande passante
1e étape. Calcul du facteur de qualité du filtre :
Formule : 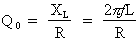
Où : f = f0 = 14 536 Hz
et L = 120 mH
Ou :
Donc : 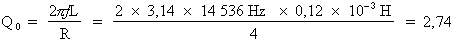
2e étape.
Calcul de la largeur de la bande passante
du filtre :
Formule : 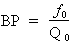
Où : f0 = 14 536 Hz et Q0 = 2,74
Donc : 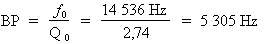
La bande passante du filtre est égale à 5 305 Hz.
3.
a) Calcul de la fréquence de coupure inférieure :
Formule : 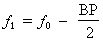
Où : f0 = 14 536 Hz
et BP = 5 305 Hz
Donc :
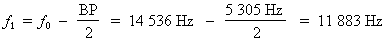
La fréquence de coupure inférieure est égale à 11 883 Hz.
b) Calcul de la fréquence de coupure supérieure :
Formule : 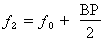
Où : f0 = 14 536 Hz
et BP = 5 305 Hz
Donc :
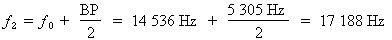
La fréquence de coupure
supérieure est égale
à 17 188 Hz.
En résumé sur le circuit RLC en série :
Après avoir étudié le contenu de cette étude, vous devriez retenir plus particulièrement les points suivants:
o L'impédance d'un circuit RLC en série est une combinaison de la résistance, de la réactance inductive et de la réactance capacitive. Elle peut être calculée par la formule générale :
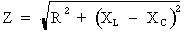
o Lorsque la réactance inductive est plus grande que la réactance capacitive (XL > XC), on observe les faits suivants :
- l'impédance se comporte comme celle d'un circuit RL ;
- la tension de la bobine est plus grande que celle du condensateur (UL > UC) ;
- le courant total du circuit est en retard de phase par rapport à la tension appliquée au circuit ;
- le circuit est considéré comme surtout inductif ;
- le facteur de puissance est un facteur inductif.
o Lorsque la réactance inductive est plus petite que la réactance capacitive (XL < XC), on note les faits suivants :
- l'impédance se comporte comme celle d'un circuit RC ;
- la tension de la bobine est plus petite que celle du condensateur (UL < UC) ;
- le courant total du circuit est en avance de phase par rapport à la tension appliquée au circuit ;
- le circuit est considéré comme surtout capacitif ;
- le facteur de puissance est un facteur capacitif.
o Lorsque la réactance inductive est égale à la réactance capacitive (XL = XC), on constate les faits suivants :
- l'impédance est à son minimum et est égale à la résistance ;
- la tension de la bobine est égale à celle du condensateur (UL = UC) ;
- le courant total du circuit et la tension appliquée sont en phase ;
- le circuit est en résonance ;
- le facteur de puissance est égal à l'unité ;
- le gain de tension du circuit (coefficient de surtension) est déterminé par :
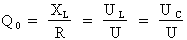
o La correction du facteur de puissance a pour but de ramener ce facteur à une valeur très près de l'unité. Toutefois, la correction du facteur de puissance par l'ajout dans le circuit d'un composant réactif (condensateur ou bobine) raccordé en série est à éviter, puisqu'il fait augmenter le courant du circuit.
o Une des applications du circuit RLC en résonance est le filtre passe-bande. La caractéristique principale d'un filtre passe-bande est de laisser passer les courants de fréquence de résonance du circuit et de rejeter tous ceux des autres fréquences.
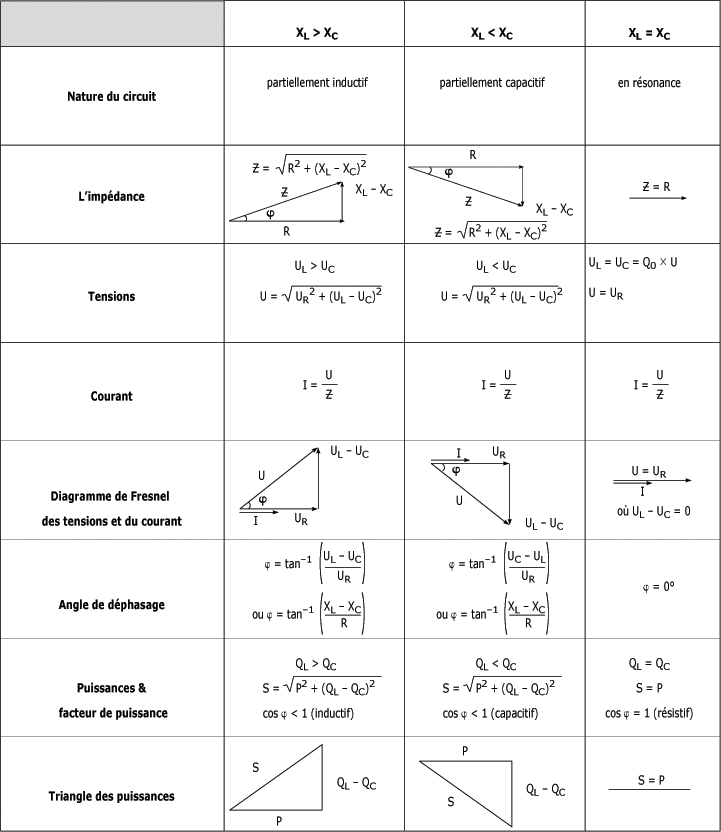
Voici un tableau récapitulatif des notions étudiées dans l'étude sur le circuit RLC en série. Celui-ci vous présente les principales caractéristiques d'un circuit RLC en série.
Vous connaissez maintenant les notions relatives aux circuits RLC en série. Une étude, vous permet d'étudier celles qui se rapportent aux circuits RLC en parallèle.
Tableau récapitulatif des caractéristiques du circuit RLC en série :
Vous avez obtenu75%de bonnes réponses !