Statistiques : Etendue, médiane, quartiles
- Fiche de cours
-
Quiz
1
- Profs en ligne
- Videos
- Application mobile
Objectif
En statistique, on manipule parfois de très grandes
quantités d’informations. Pour en simplifier
l’analyse et en donner une répartition assez
fidèle, on effectuera quelques calculs :
étendue, médiane et quartiles.
Comment calculer l’étendue, la médiane et les quartiles d’une série statistique ?
Comment calculer l’étendue, la médiane et les quartiles d’une série statistique ?
1. Etendue d'une série statistique
L’étendue d’une série
statistique est la différence entre la valeur la
plus grande et la valeur la plus petite de cette
série.
Exemple : Dans une classe de 25 élèves, on a répertorié le nombre de frères et sœurs de chaque élève dans un tableau :
| Nombre de frères et soeurs | 0 | 1 | 2 | 3 | 4 |
| Effectifs | 2 | 8 | 9 | 5 | 1 |
Etendue = 4 – 0 = 4.
L’étendue de cette série statistique est donc de 4.
Remarque : L’étendue est un indicateur de la dispersion des valeurs de cette série statistique.
2. Médiane d'une série statistique
La médiane d’une série
statistique ordonnée est la valeur qui
sépare cette série en deux groupes
de même effectif.
Exemple : Dans cette même classe de 25 élèves, on a réécrit le nombre de frères et sœurs de chacun des élèves dans l’ordre croissant :
La classe comporte 25 élèves. La 13ème valeur de cette série classée par ordre croissant sépare donc l’effectif en deux parties égales. On obtient ainsi la médiane de cette série.
Dans notre exemple, la médiane de cette série est donc 2. Ce qui signifie que la moitié des élèves a au plus ou égale 2 frères et sœurs. De même l’autre moitié a au moins ou égale 2 frères et sœurs.
Remarques :
• Dans le cas d’un effectif pair, on pourra prendre comme médiane une valeur comprise entre les deux valeurs centrales :
Exemple : considérons la série composée de 6 valeurs :
On prendra donc une valeur de la médiane entre 7 et 9, par exemple : 8.
• Attention de ne pas mélanger médiane et moyenne d’une série statistique !
Dans le cas précédent, la moyenne est de 1,8 frères sœurs par élève
(voir fiche statistique : "Effectifs, fréquences, moyenne, diagrammes")
3. Quartiles d'une série statistique
Le premier quartile d’une série
statistique ordonnée est la valeur qui sépare
cette série en deux groupes :
• Le premier groupe contient un quart des effectifs (25 %)
• Le deuxième groupe contient trois quarts des effectifs (75 %)
Le troisième quartile d’une série statistique ordonnée est la valeur qui sépare cette série en deux groupes :
• Le premier groupe contient trois quarts des effectifs (75 %)
• Le deuxième groupe contient un quart des effectifs (25 %)
Remarque : La médiane d’une série statistique correspond au deuxième quartile, les deux premiers quarts étant égaux à la moitié (50%).
Exemple 1 : Dans la classe de 25 élèves précédente, on a réécrit le nombre de frères et sœurs de chacun des élèves dans l’ordre croissant :
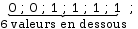 1
1
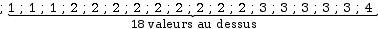
Un quart des valeurs est au dessous de la 7ème valeur et trois quarts se situent au dessus. Par conséquent, la 7ème valeur correspond au premier quartile de cette série.
Le premier quartile est donc de 1 frère ou sœur.
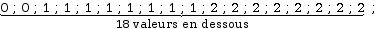 2
2 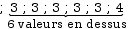
Un quart des valeurs est au dessus de la 19ème valeur et trois quarts se situent au dessous. Par conséquent la 19ème valeur correspond au troisième quartile de cette série.
Le troisième quartile est donc de 2 frères ou sœurs.
Exemple 2 : Approche graphique des quartiles et de la médiane
Dans cette même classe de 25 élèves, on note la taille des élèves dans un tableau en les regroupant par classe :
Ce tableau signifie que :
0 % des élèves mesurent moins de 150 cm
12 % des élèves mesurent moins de 160 cm
56 % des élèves mesurent moins de 170 cm
88 % des élèves mesurent moins de 180 cm
100 % des élèves mesurent moins de 190 cm
On trace un graphique de fréquences cumulées en plaçant les points de coordonnées : (0;150) ; (12;160) ; (56;170) ; (88;180) ; (12;100). Puis on relie par des segments ces différents points :
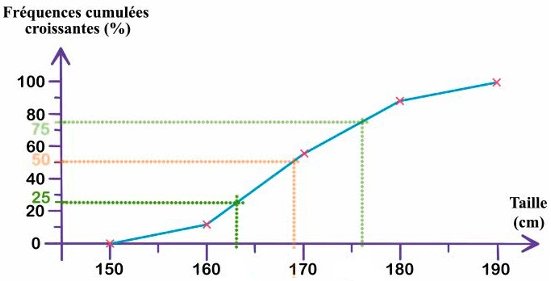
Ainsi, on peut lire graphiquement une valeur approchée de la médiane (50 %) , du premier quartile (25 %) et du troisième quartile (75 %) :
• le premier quartile est aux environs de 163 cm.
• la médiane est aux environs de 169 cm.
• le troisième quartile est aux environs de 176 cm.
• Le premier groupe contient un quart des effectifs (25 %)
• Le deuxième groupe contient trois quarts des effectifs (75 %)
Le troisième quartile d’une série statistique ordonnée est la valeur qui sépare cette série en deux groupes :
• Le premier groupe contient trois quarts des effectifs (75 %)
• Le deuxième groupe contient un quart des effectifs (25 %)
Remarque : La médiane d’une série statistique correspond au deuxième quartile, les deux premiers quarts étant égaux à la moitié (50%).
Exemple 1 : Dans la classe de 25 élèves précédente, on a réécrit le nombre de frères et sœurs de chacun des élèves dans l’ordre croissant :
Un quart des valeurs est au dessous de la 7ème valeur et trois quarts se situent au dessus. Par conséquent, la 7ème valeur correspond au premier quartile de cette série.
Le premier quartile est donc de 1 frère ou sœur.
Un quart des valeurs est au dessus de la 19ème valeur et trois quarts se situent au dessous. Par conséquent la 19ème valeur correspond au troisième quartile de cette série.
Le troisième quartile est donc de 2 frères ou sœurs.
Exemple 2 : Approche graphique des quartiles et de la médiane
Dans cette même classe de 25 élèves, on note la taille des élèves dans un tableau en les regroupant par classe :
| Taille en cm | [0;150[ | [150;160[ | [160;170[ | [170;180[ | [180;190[ |
| Effectifs | 0 | 3 | 11 | 8 | 3 |
| Fréquences en pourcentage (%) | 0 | 12 | 44 | 32 | 12 |
| Fréquences cumulées (%) | 0 | 12 | 56 | 88 | 100 |
Ce tableau signifie que :
0 % des élèves mesurent moins de 150 cm
12 % des élèves mesurent moins de 160 cm
56 % des élèves mesurent moins de 170 cm
88 % des élèves mesurent moins de 180 cm
100 % des élèves mesurent moins de 190 cm
On trace un graphique de fréquences cumulées en plaçant les points de coordonnées : (0;150) ; (12;160) ; (56;170) ; (88;180) ; (12;100). Puis on relie par des segments ces différents points :

Ainsi, on peut lire graphiquement une valeur approchée de la médiane (50 %) , du premier quartile (25 %) et du troisième quartile (75 %) :
• le premier quartile est aux environs de 163 cm.
• la médiane est aux environs de 169 cm.
• le troisième quartile est aux environs de 176 cm.
Teste dès maintenant tes nouvelles connaissances dans notre quiz
Vous avez obtenu75%de bonnes réponses !








